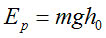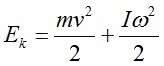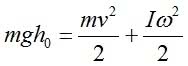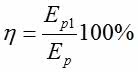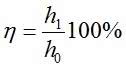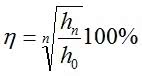Magnetyczne koło Maxwella

Wspomniany przyrząd nazywa się kołem lub wahadłem Maxwella. Zajmiemy się jego dwoma wersjami. Najpierw będzie ta wynaleziona przez Maxwella - nazwijmy ją klasyczną, w której nie ma magnesów. Później omówimy wersję zmodyfikowaną, jeszcze bardziej zadziwiającą. Obie opcje nie tylko będziemy mogli wykorzystać do pokazów, czyli doświadczeń o charakterze jakościowym, ale również przy ich użyciu wyznaczyć sprawność. Wielkość ta jest ważnym parametrem każdego silnika i maszyny roboczej.

Zaczynamy od klasycznej wersji koła Maxwella

Rys. 1. Klasyczna wersja koła Maxwella: 1 - poziomy pręt, 2 - mocna nić, 3 - oś, 4 - koło o dużym momencie bezwładności.

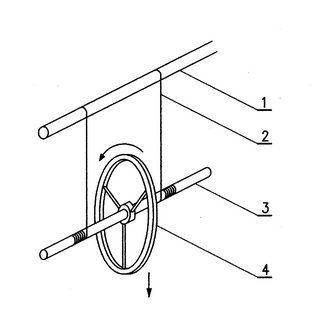
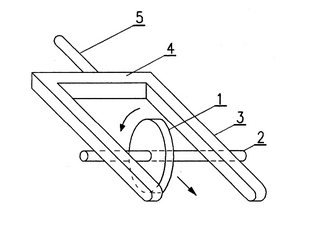
Klasyczna wersja koła Maxwella została pokazana na rys. 1. Żeby ją wykonać, mocujemy poziomo solidny pręt - może to być kij od szczotki, przywiązany do oparcia krzesła. Następnie trzeba przygotować odpowiednie koło i osadzić je nieruchomo na cienkiej osi. Najlepiej, żeby średnica koła wynosiła ok. 10-15 cm, a masa ok. 0,5 kg. Ważne jest, żeby prawie cała masa koła znajdowała się na obwodzie. Inaczej mówiąc, koło powinno mieć lekką część środkową i ciężką obręcz. W tym celu można wykorzystać małe kółko ze szprychami od jakiegoś wózka lub dużą blaszaną zakrętkę od słoika i obciążyć je na obwodzie odpowiednią ilością zwojów drutu. Koło osadzamy nieruchomo na cienkiej osi, w połowie jej długości. Oś stanowi kawałek aluminiowej rurki lub pręta o średnicy 8-10 mm. Najłatwiej - po wywierceniu w kole otworu o średnicy o 0,1-0,2 mm mniejszej niż średnica osi, albo wykorzystaniu otworu już istniejącego - wcisnąć koło na oś. Dla lepszego połączenia z kołem, oś przed wciśnięciem można posmarować klejem w miejscu kontaktu tych elementów.

Po obu stronach koła do osi przywiązujemy kawałki cienkiej i mocnej nici o długości 50-80 cm. Pewniejsze zamocowanie daje jednak przewiercenie osi w pobliżu obu końców cienkim wiertłem (1-2 mm) wzdłuż jej średnicy, przełożenie nici przez te otworki i jej zawiązanie. Pozostałe końce nici przywiązujemy do pręta i w ten sposób zawieszamy koło. Ważne jest, żeby oś koła była dokładnie pozioma, a nici pionowe i równo oddalone od jego płaszczyzny. Dla pełnej informacji należy dodać, że można również kupić gotowe koło Maxwella w firmach zajmujących się sprzedażą pomocy naukowych lub zabawek edukacyjnych. Kiedyś było ono na wyposażeniu prawie każdej szkolnej pracowni fizycznej. 

Pierwsze eksperymenty

Zaczynamy od sytuacji, w której koło zwisa na poziomej osi w najniższym położeniu, czyli obie nici są całkowicie odwinięte. Chwytamy oś koła palcami w pobliżu obu końców i obracamy ją powoli. W ten sposób nawijamy nici na oś. Należy zwrócić uwagę na układanie kolejnych zwojów nici równo - jeden przy drugim. Oś koła powinna być przy tym cały czas pozioma. Gdy koło znajdzie się w pobliżu pręta, przerywamy nawijanie i puszczamy oś swobodnie. Pod działaniem ciężaru W koło zaczyna ruch w dół i nici odwijają się z osi. Na początku koło obraca się bardzo powoli, a potem coraz szybciej. Gdy nici rozwiną się całkowicie, koło osiąga najniższe położenie i wtedy zachodzi coś zadziwiającego. Obrót koła trwa dalej w tym samym kierunku i zaczyna ono poruszać się ku górze, a nici nawijać na jego oś. Prędkość koła stopniowo maleje i w końcu się staje równa zeru. Wtedy wydaje się, że koło jest na tej samej wysokości, co przed puszczeniem swobodnie. Dalej opisane ruchy w dół i w górę powtarzają się wielokrotnie. Po kilku lub kilkunastu takich ruchach zauważymy jednak, że wysokości, na które wznosi się koło, są coraz mniejsze. W końcu koło zatrzyma się w najniższym położeniu. Przed tym można często zaobserwować wahania osi koła w kierunku prostopadłym do nici, jak w przypadku wahadła fizycznego. Stąd też koło Maxwella bywa czasem nazywane wahadłem.

Rys. 2. Podstawowe parametry koła Maxwella: m - masa, R - promień koła, r - promień osi, W - ciężar koła wraz z osią, v - prędkość liniowa, h₀ - wysokość początkowa.

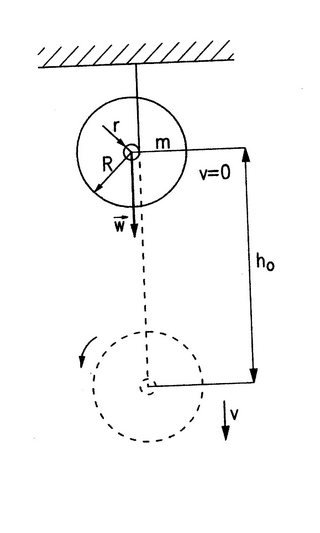
Wyjaśnimy teraz, dlaczego koło Maxwella tak się zachowuje. Nawijając nici na oś, podnosimy koło na wysokość h₀ i wykonujemy przez to pracę (rys. 2). W wyniku tego, koło w najwyższym położeniu ma energię potencjalną ciężkości E_p, wyrażającą się wzorem [1]:

w którym g oznacza przyspieszenie ziemskie.

Podczas odwijania się nici wysokość maleje, a wraz nią energia potencjalna ciężkości. Koło jednak nabiera prędkości i przez to uzyskuje energię kinetyczną E_k, którą obliczamy ze wzoru [2]:

gdzie I - oznacza moment bezwładności koła, zaś ω - jego prędkość kątową (ω = v/R). W najniższym położeniu koła (h₀ = 0) energia potencjalna też równa się zero. Energia ta jednak nie zginęła, tylko zmieniła się w energię kinetyczną, co można zapisać wzorem [3]:

Gdy koło porusza się dalej ku górze, jego prędkość maleje, ale wzrasta wysokość i wtedy energia kinetyczna zamienia się na potencjalną. Zamiany te mogłyby trwać dowolnie długo, gdyby nie opory ruchu - opór powietrza, opór związany z nawijaniem nici, które wymagają wykonania pewnej pracy i powodują zmniejszanie prędkości koła, aż do jego zatrzymania. Energia przy tym nie gnie, ponieważ praca wykonana podczas pokonywania oporów ruchu powoduje wzrost energii wewnętrznej układu i związany z tym wzrost temperatury, co można by wykryć przy użyciu bardzo czułego termometru. Praca mechaniczna może bez ograniczeń zamieniać się na energię wewnętrzną. Niestety, odwrotny proces jest ograniczony przez drugą zasadę termodynamiki i dlatego w końcowym efekcie energia potencjalna i kinetyczna koła maleje. Widać stąd, że koło Maxwella jest bardzo dobrym przykładem, pozwalającym pokazać przemiany energii i wyjaśnić zasadę jej zachowania.

Sprawność, jak to obliczyć?

Sprawność η dowolnej maszyny, urządzenia, układu lub procesu definiuje się jako iloraz energii otrzymanej w użytecznej postaci E_u do energii dostarczonej E_d. Wielkość ta wyrażana jest zwykle w procentach, stąd też sprawność zapisuje się przy pomocy wzoru [4]:

                                                        .

Sprawność rzeczywistych obiektów, czy procesów jest zawsze mniejsza niż 100%, choć może i powinna być do tej wartości bardzo zbliżona. Podaną definicję zilustrujemy prostym przykładem.

Użyteczną energią, pochodzącą z silnika elektrycznego jest energia kinetyczna ruchu obrotowego. Żeby taki silnik działał, trzeba dostarczać do niego energię elektryczną, np. z baterii. Jak wiadomo, część dostarczonej energii powoduje ogrzewanie uzwojeń, czy też potrzebna jest do pokonania sił tarcia w łożyskach. Stąd też użyteczna energia kinetyczna jest mniejsza niż dostarczona energia elektryczna. Zamiast energii do wzoru [4] można również podstawić wartości pracy.

Jak ustaliliśmy wcześniej, koło Maxwella przed rozpoczęciem ruchu ma energię potencjalną ciężkości E_p. Po zakończeniu jednego cyklu ruchów w dół i z powrotem do góry, koło również ma energię potencjalną ciężkości, ale znajduje się na mniejszej wysokości h₁, więc energia ta jest mniejsza. Oznaczmy tę energię przez E_p1. Zgodnie ze wzorem [4], sprawność naszego koła jako przetwornika energii można wyrazić wzorem [5]:

Ze wzoru [1] wynika, że energie potencjalne są wprost proporcjonalne do wysokości. Gdy podstawimy wzór [1] do wzoru [5] i uwzględnimy odpowiednie oznaczenia wysokości h oraz h₁, wówczas otrzymamy [6]:

Wzór [6] pozwala nam w bardzo prosty sposób wyznaczyć sprawność koła Maxwella -wystarczy w tym celu zmierzyć odpowiednie wysokości i obliczyć ich iloraz. Po jednym cyklu ruchów wysokości mogą jeszcze być bardzo zbliżone do siebie. Taka sytuacja może się zdarzyć w przypadku starannie zbudowanego koła o dużym momencie bezwładności, podniesionego na znaczną wysokość. Trzeba by więc wykonać pomiary z dużą dokładnością, co będzie trudne w warunkach domowych przy użyciu linijki. Można, co prawda, powtarzać pomiary i obliczać wartość średnią, ale szybciej uzyskamy wynik po wyprowadzeniu wzoru, uwzględniającego wysokość po większej liczbie ruchów. Gdy powtórzymy wcześniejsze postępowanie dla n cykli ruchu, po których koło osiągnie maksymalną wysokość h_n, wtedy wzór na sprawność będzie miał postać [7]:

Wysokość h_n po kilku lub kilkunastu cyklach ruchu na tyle dużo rożni się od h₀, że zauważenie tego i pomiar nie spowodują trudności. Sprawność koła Maxwella, zależnie od szczegółów jego wykonania - rozmiarów, masy, rodzaju i grubości nici itd. - wynosi zwykle 50-96%. Mniejsze wartości otrzymuje się w przypadku kół o małych masach i promieniach, zawieszonych na sztywniejszych niciach. Jest oczywiste, że po dostatecznie dużej liczbie cykli koło zatrzymuje się w najniższym położeniu, czyli h_n = 0. Uważny Czytelnik stwierdzi jednak, że sprawność obliczona ze wzoru [7] wynosi wtedy 0. Problem polega na tym, że wyprowadzając wzór [7], przyjęliśmy milcząco dodatkowe założenie upraszczające. Zgodnie z nim, w każdym cyklu ruchu koło traci taką samą część posiadanej aktualnie energii i jego sprawność jest stała. Mówiąc językiem matematyki, przyjęliśmy, że kolejne wysokości tworzą ciąg geometryczny o ilorazie η. W rzeczywistości tak być nie musi przed ostatecznym zatrzymaniem koła, gdy wysokości są małe. Ta sytuacja jest przykładem ogólnej prawidłowości, zgodnie z którą wszystkie wzory, prawa i teorie fizyczne mają ograniczony zakres stosowalności, zależny od założeń i uproszczeń przyjętych podczas ich formułowania.

Wersja magnetyczna

Rys. 3. Magnetyczne koło Maxwella: 1 - koło o dużym momencie bezwładności, 2 - oś z magnesami, 3 - stalowa prowadnica, 4 - łącznik, 5 - pręt.

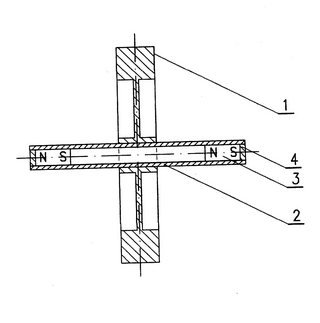
Zajmiemy się teraz magnetyczną wersją koła Maxwella - szczegóły konstrukcji przedstawiają rys. 3 i 4. Do jego zbudowania będą potrzebne dwa magnesy neodymowe w kształcie walców o średnicy 6-10 mm i długości 15-20 mm. Oś koła zrobimy z rurki aluminiowej o średnicy wewnętrznej równej średnicy magnesów. Ścianka rurki powinna być cienka - wystarczy
1 mm. Magnesy wsuwamy do rurki, umieszczając je w odległości 1-2 mm od jej końców, i przyklejamy klejem epoksydowym, np. Poxipol. Orientacja biegunów magnesów nie ma znaczenia. Końce rurki zakrywamy małymi krążkami aluminiowymi, co spowoduje, że magnesy staną się niewidoczne i oś będzie wyglądała jak jednolity pręt. Warunki, które powinno spełniać koło i sposób jego osadzenia, są takie same, jak poprzednio.

Do tej wersji koła trzeba jeszcze zrobić stalowe prowadnice z dwóch równolegle zamocowanych kształtowników. Przykładowa długość prowadnic, wygodnych w praktycznym użyciu, to 50-70 cm. Najlepiej nadają się do tego celu tzw. profile zamknięte (puste w środku) o przekroju kwadratowym, którego bok ma długość 10-15 mm. Odległość między prowadnicami powinna być równa odległości magnesów umieszczonych w osi. Końce prowadnic po jednej stronie należy opiłować półkoliście. Dla lepszego utrzymania osi można przed opiłowaniem wcisnąć w prowadnice kawałki stalowego pręta. Pozostałe końce obu prowadnic należy przymocować do łącznika z prętem w dowolny sposób, np. za pomocą śrub z nakrętkami. Dzięki temu otrzymaliśmy wygodny uchwyt do trzymania w dłoni lub zamocowania na statywie. Wygląd zewnętrzny jednego z wykonanych egzemplarzy magnetycznego koła Maxwella przedstawia fot. 1.

Żeby uruchomić magnetyczne koło Maxwella, przykładamy końce jego osi do górnych powierzchni prowadnic w pobliżu łącznika. Trzymając prowadnice za uchwyt, pochylamy je ukośnie w kierunku zaokrąglonych końców. Wówczas koło zaczyna staczać się po prowadnicach, podobnie jak po równi pochyłej. Po osiągnięciu zaokrąglonych końców prowadnic koło nie spada, ale przetacza się po nich i

Rys. 4. Szczegóły budowy magnetycznego koła Maxwella pokazane w przekroju osiowym:
1 - koło o dużym momencie bezwładności, 2 - oś z rurki aluminiowej, 3 - magnes neodymowy w kształcie walca, 4 - krążek aluminiowy.

wykonuje zadziwiającą ewolucję - wtacza się ku górze po dolnych powierzchniach prowadnic. Opisany cykl ruchów powtarza się wiele razy, podobnie jak w przypadku klasycznej wersji koła Maxwella. Prowadnice możemy nawet ustawić pionowo, a i tak koło będzie zachowywało się analogicznie. Utrzymywanie się koła na powierzchniach prowadnic jest możliwe dzięki przyciąganiu osi przez ukryte w niej magnesy neodymowe.

Gdyby przy dużym kącie nachylenia prowadnic koło ślizgało się po nich, wtedy końce jego osi wystarczy owinąć jedną warstwą drobnoziarnistego papieru ściernego i przykleić go klejem „Butapren”. W ten sposób zwiększymy tarcie, niezbędne do zapewnienia toczenia się bez poślizgu. Podczas ruchu magnetycznej wersji koła Maxwella zachodzą analogiczne przemiany energii mechanicznej, jak w przypadku wersji klasycznej. Straty energii mogą być jednak nieco większe z powodu występowania tarcia i przemagnesowywania prowadnic. Dla tej wersji koła możemy również wyznaczyć sprawność w sposób podobny, jak opisany wcześniej dla wersji klasycznej. Interesujące będzie porównanie uzyskanych wartości. Łatwo się domyślić, że prowadnice wcale nie muszą mieć kształtu prostoliniowego (mogą być np. faliste) i wtedy ruch koła będzie jeszcze bardziej interesujący.

Perpetuum mobile i magazyny energii

Doświadczenia przeprowadzone z kołem Maxwella pozwalają na wyciągnięcie kilku wniosków. Najważniejszy z nich jest taki, że przemiany energii są w przyrodzie zjawiskiem bardzo powszechnym. Zawsze wiążą się z nim tzw. straty energii, tak naprawdę będące przemianami na takie rodzaje energii, które w danej sytuacji nie są dla nas użyteczne. Z tego powodu sprawność rzeczywistych maszyn, urządzeń i procesów jest zawsze mniejsza niż 100%. Również dlatego nie można zbudować perpetuum mobile, czyli urządzenia, które raz wprawione w ruch poruszałoby się wiecznie, bez dostarczania energii z zewnątrz, niezbędnej do pokrycia strat. Niestety, w XXI w. nie wszyscy jeszcze zdają sobie z tego sprawę. Dlatego od czasu do czasu do Urzędu Patentowego RP wpływa projekt wynalazku w rodzaju „Uniwersalne urządzenie do napędu maszyn”, które wykorzystuje „niewyczerpaną” energię magnesów (w innych krajach pewnie też się to zdarza). Oczywiście, takie zgłoszenia załatwiane są odmownie. Uzasadnienie jest krótkie: urządzenie nie będzie działać i nie nadaje się do przemysłowego zastosowania (nie spełnia więc koniecznych warunków uzyskania patentu), ponieważ jest niezgodne z podstawowym prawem przyrody - zasadą zachowania energii.

Fot. 1. Wygląd zewnętrzny jednego z magnetycznych kół Maxwella.

Czytelnicy być może zauważą pewną analogię między kołem Maxwella a popularną zabawką o nazwie jo-jo. W przypadku jo-jo straty energii są uzupełniane pracą, wykonywaną przez użytkownika tej zabawki, który rytmicznie podnosi i opuszcza górny koniec nici. Ważny jest również wniosek, że ciało o dużym momencie bezwładności trudno wprawić w ruch obrotowy i trudno je zatrzymać. Stąd też koło Maxwella powoli nabiera prędkości podczas ruchu w dół i również powoli ją zmniejsza, wznosząc się ku górze. Długo powtarzają się też cykle ruchów „góra-dół”, zanim nastąpi ostateczne zatrzymanie koła. Wszystko to dlatego, że w takim kole zmagazynowana jest duża energia kinetyczna. Stąd też rozpatrywane są projekty zastosowania kół, mających duży moment bezwładności i wprawionych wcześniej w bardzo szybki ruch obrotowy, jako swego rodzaju „magazynów” energii, przeznaczonych np. do uzupełniającego napędu pojazdów. Dawniej potężne koła zamachowe były używane w maszynach parowych do zapewnienia bardziej równomiernych obrotów, a dzisiaj są też nieodłącznym elementem samochodowych silników spalinowych.