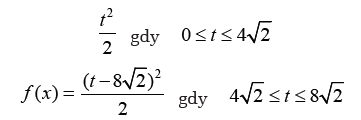Kolorowe kwadraty i zaćmienia Słońca

Artykuł opisuje moje zajęcia dla gimnazjalistów – stypendystów Krajowego Funduszu na Rzecz Dzieci. Fundusz wyszukuje dzieci i młodzież wybitnie zdolną (od V klasy szkoły podstawowej do maturalnej) i oferuje wybranym podopiecznym „stypendia”. Nie polegają one jednak wcale na wypłacie gotówki, tylko na wszechstronnej opiece nad rozwojem talentu, na ogół przez wiele lat. W odróżnieniu od wielu innych przedsięwzięć tego typu, podopieczni Funduszu są poważnie traktowani przez znanych naukowców, twórców kultury, wybitnych humanistów i innych mądrych ludzi, a także przez niektórych polityków.

Działalność Funduszu rozpościera się na wszystkie dyscypliny będące podstawowymi przedmiotami szkolnymi, wyłączając sport, a włączając kierunki artystyczne. Fundusz powstał w 1983 r., jako odtrutka na ówczesną rzeczywistość. Do Funduszu może zgłosić się każdy (zwykle za pośrednictwem szkoły, najlepiej do końca roku szkolnego), ale oczywiście jest pewne sito, pewna procedura kwalifikacji.

Jak wspomniałem, artykuł jest oparty na moich zajęciach warsztatowych, konkretnie w Gdyni, w marcu 2016 r., w 24. Gimnazjum przy III LO im. Marynarki Wojennej. Od wielu lat warsztaty te organizuje – pod egidą Funduszu – Wojciech Tomalczyk, nauczyciel o nadzwyczajnej charyzmie i wysokim poziomie intelektualnym. W 2008 r. znalazł się w pierwszej dziesiątce osób w Polsce, którym nadano (przewidziany w ustawie sprzed wielu lat) tytuł profesora oświaty. Niewiele jest przesady w stwierdzeniu: „Oświata, to oś świata”.

Zaćmienia Słońca i Księżyca są zawsze fascynujące – można wtedy poczuć, że żyjemy na malutkiej planecie w ogromnej przestrzeni, gdzie wszystko jest w ruchu, wymierzone do centymetrów i sekund. Mnie to trochę nawet przeraża, również perspektywy czasowe. Dowiadujemy się oto, że najbliższe zaćmienie całkowite, widoczne z obszaru obecnej Warszawy, będzie w… 2681 r. Ciekawe, kto je zobaczy? Pozorne wielkości Słońca i Księżyca na naszym niebie są niemal takie same – dlatego zaćmienia są tak krótkie i tak efektowne. Przez wieki te krótkie minuty musiały wystarczyć astronomom jako jedyna sposobność ujrzenia korony słonecznej. Dziwne, że zdarzają się one dwa razy do roku… to znaczy jednak tylko tyle, że gdzieś na Ziemi przez krótki okres można je dostrzec. Wskutek ruchów pływowych Księżyc oddala się od Ziemi – za 260 mln lat będzie tak daleko, że będziemy (my???) oglądać już tylko zaćmienia obrączkowe.

Podobno pierwszym, który przewidział zaćmienie Słońca, był Tales z Miletu (VII-VI wiek p.n.e.). Nie dowiemy się zapewne, czy naprawdę tak było, to znaczy, czy przewidział, bo to, że zaćmienie w Azji Mniejszej miało miejsce 28 maja 585 r. p.n.e., jest faktem potwierdzonym współczesnymi obliczeniami. Oczywiście dane podaję wg dzisiejszej rachuby czasu. Gdy byłem dzieckiem, wyobrażałem sobie, że ludzie wtedy liczyli lata „do tyłu”. Jest więc np. rok 567 przed naszą erą, przychodzi wieczór sylwestrowy i ludzie się cieszą: już tylko 566 lat do „naszej ery”! A jak się musieli cieszyć, gdy wreszcie nastała „nasza era”! Co tam przełom tysiącleci, jaki kilkanaście lat temu przeżyliśmy!

Matematyka, stojąca za obliczeniami dat i zasięgu zaćmień, nie jest specjalnie skomplikowana, tylko nafaszerowana najrozmaitszymi czynnikami, związanymi z regularnością i, co gorsza, nieregularnością ruchów ciał po orbitach. Żałuję nawet, że tej matematyki nie znam. Jak mógł stosowne rachunki wykonać Tales z Miletu? Odpowiedź jest prosta. Trzeba mieć mapę nieba. Jak zrobić taką mapę? To też nietrudne, umieli to starożytni Egipcjanie. O północy wychodzi na dach świątyni dwóch kapłanów. Każdy z nich siada i rysuje to, co widzi (kolegę również). Po dwóch tysiącach lat wiemy już wszystko o ruchu planet…

Ładna geometria, czyli zabawa na „dywaniku”

Grecy nie lubili liczb, uciekali do geometrii. Tak postąpimy i my. Nasze zaćmienia będą proste, kolorowe, ale równie – albo i bardziej – interesujące, jak i prawdziwe. Przyjmiemy umowę, że niebieska figura porusza się tak, by zaćmić czerwoną. Będziemy nazywać niebieską figurę Księżycem, a czerwoną Słońcem. Postawimy sobie pytania:

ile czasu trwa zaćmienie;
kiedy zasłonięta jest połowa tarczy;

Rys. 1 Kolorowy "dywanik" ze Słońcem i Księżycem
jakie jest maksymalne zakrycie;
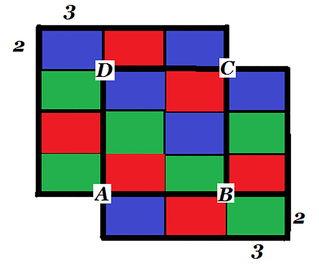
czy potrafimy zanalizować zależność zakrycia tarczy od czasu? W tym artykule (ogranicza mnie objętość tekstu) skupię się na drugim pytaniu. Stoi za tym ładna geometria, możliwie bez nudnych obliczeń. Spójrzmy na rys. 1. Czy można przypuścić, że będzie on miał związek z… zaćmieniem Słońca?

Rys. 2 "Niebieski" Księżyc i "czerwone" Słońce

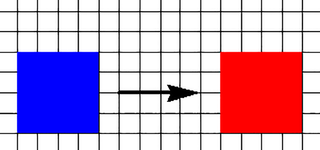
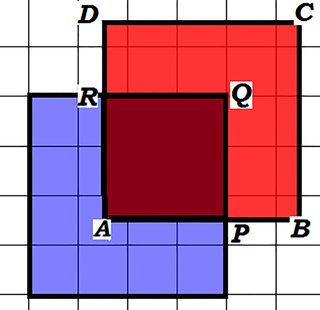
Nasze ciała niebieskie, przynajmniej na początku, będą kolorowymi kwadratami. Księżyc na niebiesko, Słońce na czerwono (najlepsze do kolorowania). Przy prawdziwym zaćmieniu Księżyc goni Słońce po niebie, dogania… i zasłania. U nas też tak będzie. Najprostszy przypadek to ten, gdy Księżyc porusza się względem Słońca tak, jak na rys. 2. Zaćmienie zaczyna się, gdy brzeg tarczy Księżyca dotknie brzegu tarczy Słońca (rys. 2), a skończy, gdy wyjdzie poza.

Rys. 3 Księżyc zbliża się do Słońca po przekątnej

Przyjmujemy, że „Księżyc” porusza się jedną kratkę na jednostkę czasu, np. minutę. Zaćmienie trwa wtedy osiem jednostek czasu, powiedzmy, minut. W połowie zaćmienia Słońce zasłonięte jest całkowicie Połowa tarczy jest zasłonięta dwukrotnie: po 2 i po 6 minutach. Wykres zależności „procent zasłonięcia” jest prosty. Przez pierwsze dwie minuty tarcza jest zasłaniana jednostajnie w tempie od zera do 1, przez następne odsłaniana w tym samym tempie.

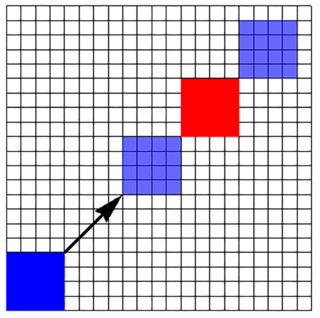
A oto bardziej interesujący przykład (rys. 3). Księżyc zbliża się do Słońca od strony przekątnej. Zgodnie z naszą umową „kratka na minutę”, zaćmienie trwa 8√2 minut – w połowie tego czasu mamy zaćmienie całkowite. Obliczmy, jaka część Słońca jest zasłonięta po czasie t (rys. 3). Jeżeli od początku zaćmienia upłynęło upłynęło t minut i w wyniku tego Księżyc znalazł się tak, jak na rys. 5, to (uwaga!) 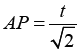zatem zasłonięte jest (pole kwadratu APQR) równe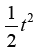Połowa tarczy słonecznej zasłonięta jest zatem wtedy, gdy 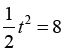a więc po 4 minutach (potem na 4 minuty przed końcem zaćmienia).

Rys. 4 Wykres funkcji "zasłonięcia"

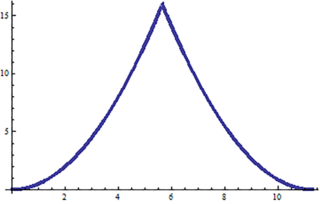
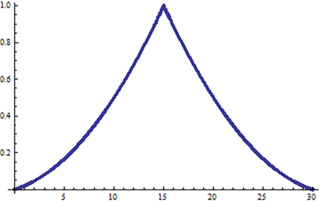
Zaćmienie całkowite trwa jedną chwilę (t=4√2), a wykres funkcji „część zasłonięta” składa się z dwóch łuków parabol (rys. 4).

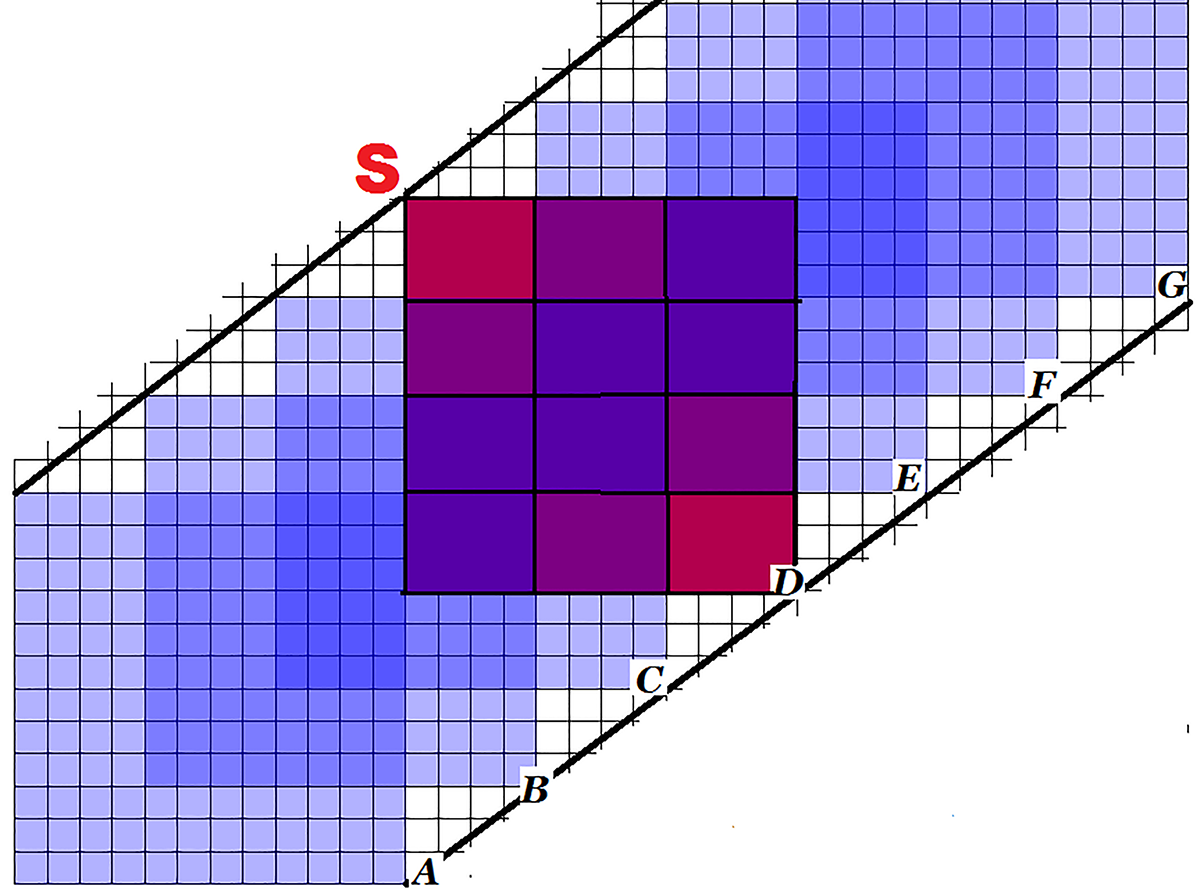
Nasz niebieski Księżyc zetknie się narożnikiem z czerwonym Słońcem, ale będzie zasłaniał go, nie idąc wzdłuż przekątnej, tylko nieco na ukos.Ciekawa geometria pojawia się, gdy trochę skomplikujemy ruch (rys. 6). Kierunkiem ruchu jest teraz wektor [4,3], czyli „cztery kratki w prawo, trzy do góry.” Położenie Słońca jest takie, że zaćmienie zaczyna się (położenie A), gdy boki „ciał niebieskich” zetkną się na jednej czwartej ich długości. Gdy Księżyc przesunie się do położenia B, zaćmi jedną szóstą Słońca, w położeniu C – połowę. W położeniu D mamy całkowite zaćmienie i następnie wszystko cofa się „tak jak przyszło”.

Rys. 5 Część Słońca zasłonięta po czasie t

Zaćmienie kończy się, gdy Księżyc jest w położeniu G. Trwało tyle czasu, ile wynosi długość odcinka AG. Jeżeli, jak poprzednio, przyjmiemy, że jednostką czasu jest czas potrzebny Księżycowi na przebycie „jednej kratki”, to długość AG jest równa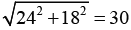 . Gdyby wrócić do poprzedniej konwencji, zgodnie z którą nasze ciała niebieskie mają rozmiary 4 na 4, wynik byłby inny (jaki?). Jak można nietrudno wykazać, po czasie t < 15 zasłonięte jest 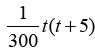tarczy. Wykres funkcji „procent zasłonięcia tarczy” widzimy na rys. 6.

Rys. 6 Wykres funkcji "procent zasłonięcia tarczy"

Zaćmienie i równanie przestępne

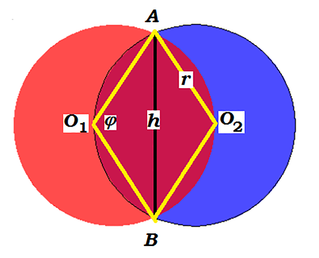
Rys. 7 Zasłonięcie tarczy Słońca w czasie zaćmienia przedstawionego na rys. 6

Zadanie o zaćmieniach byłoby niepełne, gdybyśmy nie rozpatrzyli przypadku kół. Jest to o wiele trudniejsze, ale spróbujmy wyliczyć, kiedy jedno koło zaćmi połowę drugiego – i to w najprostszym przypadku, kiedy jedno z nich porusza się po średnicy łączącej je oba. Rysunek jest znany posiadaczom pewnego rodzaju kart kredytowych.

Wyliczenie, w jakiej pozycji pola są równe, jest o tyle skomplikowane, że wymaga po pierwsze znajomości wzoru na pole odcinka kołowego, po drugie znajomości miary łukowej kąta, po trzecie (i najgorsze w tym wszystkim) umiejętności rozwiązania pewnego równania przestępnego. Nie będę wyjaśniał, co to jest „równanie przestępne”, zobaczymy na przykładzie (rys. 8).

Rys. 8 Zaćmienie "w formie kulistej"

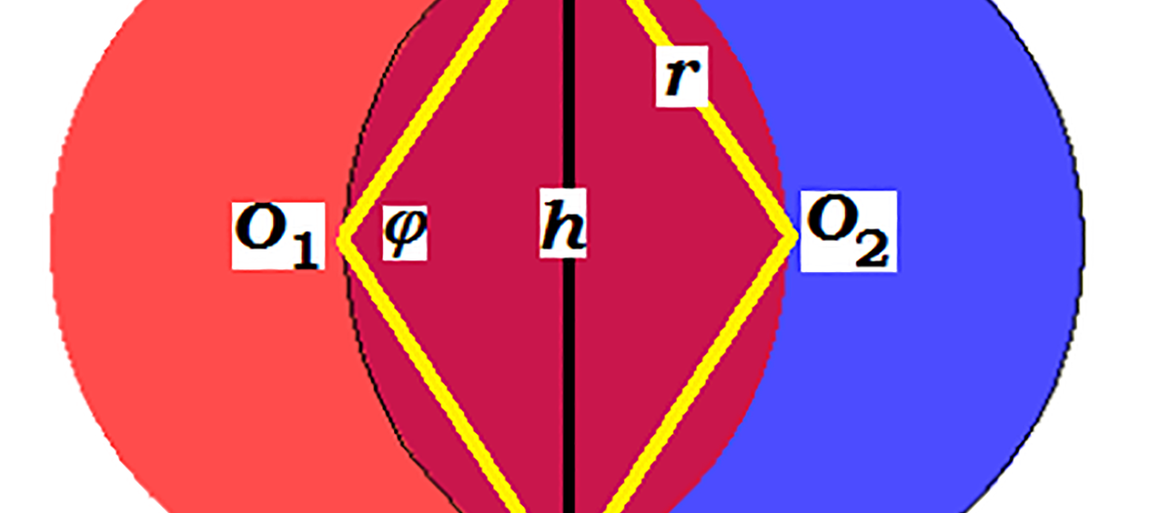
Odcinek kołowy to ta „czasza”, która zostaje po przecięciu koła linią prostą. Pole takiego odcinka jest równe S = 1/2r²(φ-sinφ), gdzie r jest promieniem okręgu, a φ – kątem środkowym, na którym oparty jest odcinek (rys. 8). Łatwo to wyprowadzić, odejmując pole trójkąta od pola wycinka kołowego.

Odcinek O₁O₂ (odległość środków okręgów) ma wtedy długość 2rcosφ/2, a wysokość (szerokość, „wcięcie w talii”) h = 2rsinφ/2. A zatem, chcąc wyliczyć, kiedy Księżyc zakryje połowę tarczy słonecznej, musimy rozwiązać równanie: które po uproszczeniach przybiera postać:

Rys. 9 Wykresy dwóch funkcji

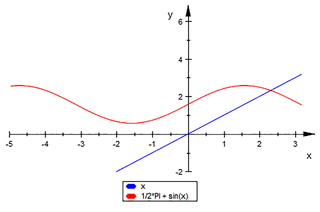
Rozwiązywanie takich równań wykracza poza zwykłą algebrę – w równaniu występują zarówno kąty, jak i ich funkcje trygonometryczne. Równanie jest poza zasięgiem tradycyjnych metod. Dlatego nazywa się przestępne. Zobaczmy najpierw wykresy obydwu funkcji, tzn. funkcji f(x) = x i funkcji 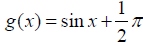Możemy z tego rysunku odczytać rozwiązanie przybliżone. Możemy jednak do przybliżenia dostać się metodą iteracyjną albo… skorzystać z opcji Solver w arkuszu kalkulacyjnym Excel. Każdy licealista powinien to umieć, mamy wszak XXI wiek. Ja skorzystałem z bardziej wyrafinowanego narzędzia, programu Mathematica i oto nasze rozwiązanie, z nikomu niepotrzebną dokładnością 20 miejsc dziesiętnych:

SetPrecision[FindRoot[x==Sin[x]+Pi/2,{x,2}],20] {x⇒2.3098814600100574523}.

Rys. 10 Animacja zaćmienia w programie matematica

Zamieniamy to na stopnie, mnożąc przez 180/π. Otrzymujemy 132 stopnie, 20 minut, 45 i ćwierć sekundy kątowej. Wyliczamy stąd, że odległość środków kół wynosi O₁O₂ = 0,808 promienia, zaś „wcięcie w talii” to 2,310.