Łamigłówki i poważne zadania

Kłopotem każdego, kto chce pisać o matematyce, jest to, że nadzwyczaj trudne – a niekiedy wręcz niemożliwe – jest samo przedstawienie wyników i omówienie ich w sposób przystępny i prawdziwy. Nader często matematycy prezentują swoje wyniki w sposób, który jest błyskotliwy i dowcipny… tylko dla nich samych. Kto np. doceni „twierdzenie o kanapkach”: bułkę z masłem i szynką można przeciąć płaskim cięciem tak, by przepołowić bułkę, masło i szynkę…? Inny przykład to twierdzenie o antypodach: w każdej chwili na Ziemi są takie dwa punkty, położone dokładnie po przeciwnych stronach, w których panuje identyczna temperatura i takie samo ciśnienie. Owszem, może to i ciekawe, ale czy właśnie na takie głupstwa marnują swój czas (i pieniądze podatnika) matematycy?
No właśnie, piękno matematyki tkwi w niej samej, a nie w ozdobnikach. To po pierwsze. Po drugie – na ogół jest tak, że badania matematyczne prędzej czy później się przydają. Nie wszystkie, nie zawsze. Nie sposób jednak przewidzieć, które i kiedy. Po trzecie – zgadzamy się na pewno, że jakiejś matematyki trzeba uczyć, w szkole i na studiach. Do tego potrzebni są… no właśnie, matematycy. Po czwarte: czy nam się to podoba, czy nie, matematyka nas oplątuje w życiu codziennym. Nie zawsze zdajemy sobie z tego sprawę.
Kasetka lady Fitzarnulph – i trochę prądu
Po tym wstępie – do rzeczy. Najpierw zadanie. Czy umiemy podzielić kwadrat (albo ogólniej – prostokąt) na mniejsze kwadraciki (prostokąciki)?
No, jasne – tak, jak kawałek czekolady na kostki. Co w tym interesującego? To prawda, niewiele. Ale… pomyślmy nad takim oto zadaniem. Tabliczka czekolady ma 6×4=24 kostki. Chcemy ją połamać na te 24 części. Ile najmniej łamań jest potrzebnych? Odpowiedź jest prosta: łamań musi być 23, ani więcej, ani mniej. Dlaczego? Za każdym łamaniem jedna część dzieli się na dwie, a zatem przybywa jedna nowa część. Aby z jednej części zrobić 24, potrzeba 23 łamań.
Ale to nie jest jeszcze specjalnie interesujące matematycznie. Jak więc można podzielić kwadrat na mniejsze kwadraty w sposób, który moglibyśmy nazwać interesującym? Na przykład tak, żeby każdy kwadracik był inny.
Kilka już razy przywoływałem w tym kąciku postać amerykańskiego intelektualisty Martina Gardnera (1914-2010), człowieka, który, nie będąc matematykiem, zrobił dla matematyki bardzo wiele dobrego. Otóż niemal samodzielnie wykreował i podtrzymywał przez długi czas zainteresowanie matematyką rekreacyjną w Stanach Zjednoczonych – co promieniowało na cały świat. Najbardziej znany jest jako columnist (redaktor) działu matematycznego w „Scient American”. Dział ten redagował w latach 1956-1981. Opowiadał, ile pracy kosztuje go każdy artykuł – porusza się bowiem w materii niezbyt mu znanej. Tym niemniej artykuły jego były rzeczowe, dalekie od zachwycania się błahostkami. Można powiedzieć, że był prawdziwym humanistą – otwartym na każdą ludzką działalność intelektualną.
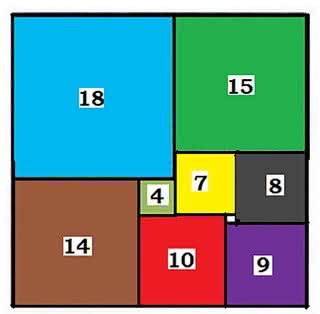
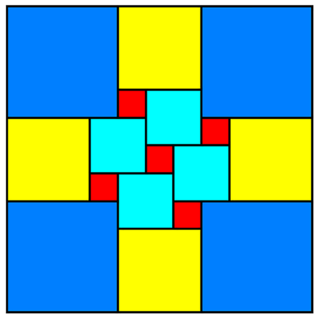
Podobną rolę odegrał wcześniej w Europie Anglik Henry Dudeney (1863-1930), autor kilkunastu książek z łamigłówkami – na ogół bardzo trudnymi (!). Zaczęło się wszystko od zadania, które Dudeney zamieścił w „The London Magazine” w styczniu 1902 r. – choć jego treścią matematyczną nie było dosłownie „podziel kwadrat na kwadraty”. W zadaniu tym występowała piękna i bogata lady Isabel de Fitzarnulph. Do jej skarbów należała kwadratowa kasetka, w której leżała sztabka złota rozmiarów ćwierć cala na 10 cali, otoczona drewnianymi kwadratowymi klockami (rys. 1). Każdy klocek miał inny rozmiar. Ojciec Izabeli przeznaczył rękę córki temu, kto odgadnie rozmiary kasetki.
Nikt z czytelników magazynu nie nadesłał rozwiązania; historia milczy, czy Izabela została starą panną. W 1905 r. Dudeney zamieścił zadanie w swoich „The Canterbury Puzzles” (zadanie nr 40) i podał nie tyle rozwiązanie, co odpowiedź, z komentarzem, że jest to jedyna konfi guracja spełniająca warunki zadania, ale samo rozumowanie pozostaje zbyt skomplikowane, by je tam zamieścić… (może margines był za mały?). Wspomniał też: „a może można podzielić kwadrat na mniejsze kwadraty, każdy inny?”.
Zadanie. Wyznacz rozmiary kwadratów widocznych na rys. 1, wiedząc, że żółty (złoty!) prostokąt ma rozmiar 1/4 cala na 10. Rozwiązania nie podam – można je odczytać z rysunku albo znaleźć w Internecie. Nie podam również dowodu, że innej możliwości nie ma – czyli, że nie da się inaczej otoczyć sztabki złota Izabelli samymi kwadratowymi klockami. Dlaczego nie podam? Bo sam tego dowodu nie znam! Może ktoś z Czytelników? Zadanie o dzieleniu kwadratu (czy ogólniej, wypełnianiu prostokąta prostokątami) wzbudziło zainteresowanie w Europie w początkach dwudziestego wieku.
Pierwszym, który podał rozwiązanie „przybliżonego” zadania, był młody lwowski (po wojnie wrocławski) matematyk Zbigniew Moroń (1904-1971). Otóż w 1925 r. opublikował on w czasopiśmie „Przegląd Matematyczny i Fizyczny” artykuł O rozkładach prostokątów na kwadraty. Jednym z wyników był rozkład na kwadraty prostokąta 32×33. Z kolei zadanie oryginalne (podział kwadratu na kwadraty) próbował bez powodzenia rozwiązać Hugo Steinhaus (1887-1972, również lwowianin, potem wrocławianin).
Zadanie wydaje się typową łamigłówką. Ale dość szybko zauważono, że ma związek z… przepływami prądu elektrycznego i nie tylko elektrycznego, a np. pociągów, samochodów i ludzi. Każdy przyzna, że tak rozumiana kontrola przepływów stanowi ważne zagadnienie we współczesnym świecie.
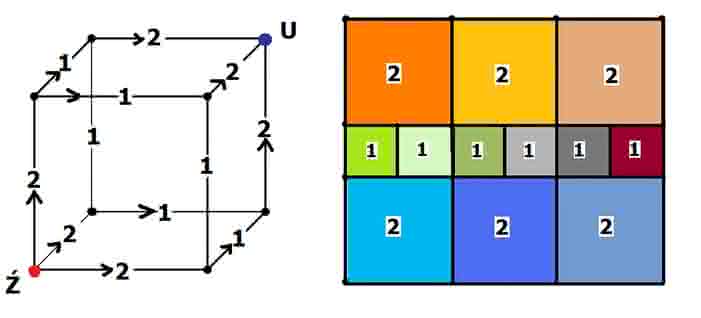
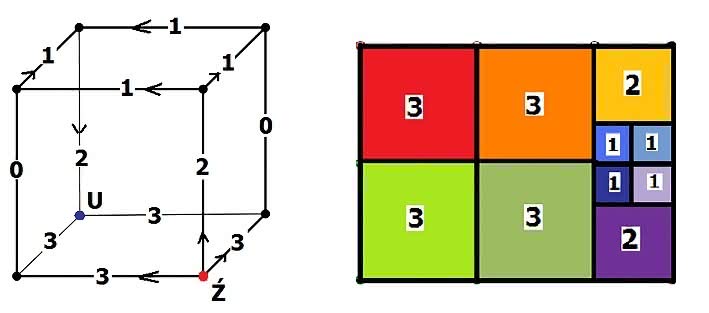
Gdzie tu prąd? Wyobraźmy sobie, że do górnego i dolnego brzegu kwadratu (ogólniej: prostokąta) podłączony jest prąd i że opór całego kwadratu wynosi R. Jeżeli kwadrat jest pocięty na prostokąty, to opór każdego kawałka będzie wprost proporcjonalny do jego długości, a odwrotnie proporcjonalny do jego szerokości. Jeżeli zatem te prostokąty są kwadratami, to ich opór jest taki sam – możemy przyjąć, że jednostkowy. Zatem każdy podział prostokąta na kwadraty generuje sieć elektryczną, złożoną z oporników o tej samej rezystancji (za moich szkolnych czasów mówiło się: oporności). Na odwrót, taka sieć wyznaczy podział prostokąta. Na rys. 4 i 5 mamy proste przykłady podziału prostokąta odpowiadające podłączeniu prądu do wierzchołków sześcianu.
Otóż na przepływ prądu można patrzeć jak na… wagony kolejowe, przetaczane po skomplikowanej sieci. Można też wyobrażać sobie, że patrzymy na sieć wyciągów narciarskich, albo na dowolną inną sieć i dowolne w niej przepływy. Przyjmujemy, że oporność jednego odcinka sieci wynosi 1 om. W interpretacji wagonowej znaczy to tyle, że każdy odcinek sieci ma przepustowość jednego wagonu (narciarza) na jednostkę czasu. Znaczy to np., że dwóch narciarzy wjedzie w czasie 2 jednostek czasu, a trzech w 3. Wszyscy muszą spotkać się jednocześnie w punkcie docelowym. A zatem rozkład kwadratu na kwadraty wyznacza pewną sieć przepływów – taką, że wszystkie wagony (ludzie, narciarze, samochody) dotrą do celu w tym samym czasie.
Podział kwadratu – czy można lepiej?
Nie wiem, jak dokładnie działa wyszukiwarka internetowa, nie wiem, jak działa telefon komórkowy i podejrzewam, że niewielu Czytelników w pełni potrafi zrozumieć, „jak to jest”. Po prostu działa i już. Tylko z literatury wiem, że gdy mówię do komórki „halo”, mój głos jest rozkładany „na czynniki pierwsze” i przesyłany w porcjach do adresata. Ważne, żeby te porcje zeszły się w tym samym momencie. Każdy, kto używ Skype’a (zwłaszcza kilka lat temu), miał na pewno kłopoty związane z tym właśnie – pewne słowa, sylaby i głoski spóźniały się. Postęp techniczny zawdzięcza wiele właśnie matematyce, która wyjaśnia, jak należy przetwarzać dane możliwie efektywnie. Być może rozcinanie kwadratu na kwadraty przydaje się w telefonii komórkowej. Być może, tego nie wiem.
W 1935 r. Stanisław Ruziewicz (1889-1941) wpisał do słynnej „Księgi Szkockiej”, jako zadanie nr 59, pytanie, czy można podzielić kwadrat na skończoną liczbę kwadratów, różnych między sobą. Mikołaj Łuzin (1883- -1950) postawił od razu hipotezę, że jest to niemożliwe. Próbując udowodnić hipotezę, Roland Percival Sprague (1894-1967) odkrył w 1939 r. coś przeciwnego (czyli, jak mówimy w matematyce, kontrprzykład) – rozkład kwadratu rozmiaru 4205×4205 na 55 mniejszych, każdy inny.
W rok później Stone i Tutte zmniejszyli liczbę kwadracików do 28, potem do 24, w 1948 r. Willcocks do 23, a w 1978 r. Adrianus Johannes Wilhelmus Duijvestijn (1927-1998) do 21. Ten ostatni matematyk (jego nazwisko jest trudne dla nas tak, jakby dla niego był Brzęczyszczykiewicz albo nawet Krzyszkowiak) wykazał, że mniej kwadracików nie wystarczy. Nie da się złożyć kwadratu z dwudziestu (lub mniej) kwadracików, gdy każdy kwadracik ma mieć inny rozmiar.
Wynik Duijvestijna nie zamknął tematyki „podziału kwadratu”. Można szukać innych rozkładów, można badać rozkłady prostokątów i liczne uogólnienia, a zawsze powstaje pytanie: czy znaleziony rozkład jest jedyny i czy można lepiej? W 1993 r., a więc prawie już ćwierć wieku temu, Jasper D. Skinner opublikował książkę „Squaring the square – who is who and what is what?” (Kwadratura kwadratu – kto jest kim i co jest czym). To pokazuje, jak duże jest zainteresowanie matematyków tym zagadnieniem, które (jak niewiele fragmentów matematyki może być zrozumiane przez każdego. W wydanej w 2011 r. książce „Mathematical Discovery”, przeznaczonej dla niematematyków, autorzy (Bruckner, Thomson, Bruckner), poświęcają zagadnieniu podziału na kwadraty obszerny rozdział – a książkę nobilituje wywiad z nie byle kim, bo z Andrew Wilesem – odkrywcą dowodu Wielkiego Twierdzenia Fermata.
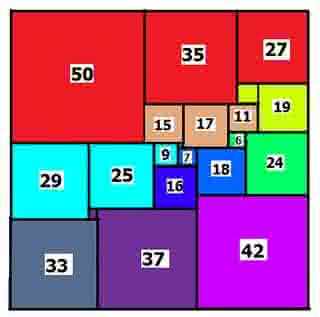
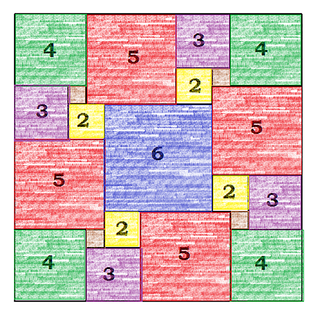
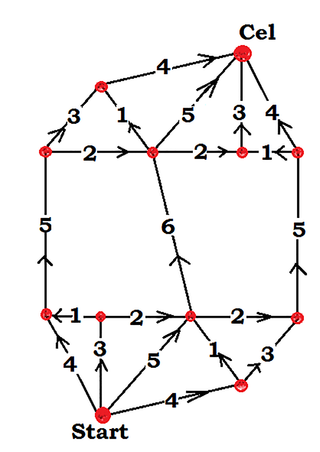
Jako przykład współczesnych badań na ten temat podam, dość losowy wybrany, całkiem niedawny wynik. Lorenz Milla z Uniwersytetu w Heidelbergu (a więc bardzo dobrej uczelni) rozwiązał następujący problem: szukajmy podziału kwadratu na kwadraty niekoniecznie różne, ale przy założeniu, że dwa takie same nie mogą mieć wspólnego boku. W 2013 r. Milla wykazał, że wśród kwadratów nie większych niż 17×17, są możliwe tylko dwa takie rozkłady: jeden dla kwadratu 12×12, drugi 16×16 (rys. 6 i 7). Na rys. 8 mamy sieć przepływów wg jednego (którego?) rozkładu Lorenza Milli. Można to rozumieć tak: z punktu na dole rozchodzi się sieć wyciągów narciarskich na górę Cel. Liczby diagramu pokazują przepustowość poszczególnych odcinków sieci. Przepustowość pokazuje, ilu narciarzy może pokonać dany odcinek w jednostce czasu, powiedzmy na minutę. Przepustowść 1 oznacza bardzo powolny odcinek – pokonanie go zajmuje minutę. W tym czasie innym odcinkiem wjedzie aż pięciu narciarzy. Zobaczmy, jaka jest przepustowość całego układu. Z dołu wyjeżdża jednocześnie szesnastu narciarzy (4+3+5+4); dzielą się oni tak, jak pokazuje diagram. Jak widać, wszyscy wjeżdżąją w jednakowym czasie, wynoszącym 16 jednostek i nigdzie nie ma zatorów ani przestojów. Przepustowość sieci wynosi 1.
Taki jest właśnie pożytek z zadań o rozcinaniu kwadratu – generują sieć przepływów o przepustowości 1.