Komputery kwantowe: wymyślić maszynę - i zadanie dla niej

W eksperymencie opisanym w internetowym serwisie „Nature” profesorowie Morgan W. Mitchell i Valerio Pruneri zbadali właściwości dwóch splątanych ze sobą elektronów „uwięzionych” w odrębnych kryształach diamentowych. Lokalny realizm nakazywałby, aby ich orientacja była w jakiś sposób zdeterminowana wcześniej i zachodziła deterministyczna komunikacja tego stanu. Jednak pomiar dokonany w eksperymencie zaprzeczył postulatowi Einsteina - orientacje elektronów były splątane i przypadkowe, a można je było określić dopiero w chwili pomiaru.
Jak zauważył na łamach „New York Timesa” kierujący eksperymentem holenderski profesor Ronald Hanson, przedsięwzięcie nie jest czczą zabawą w przekomarzanie się z Einsteinem, lecz ma praktyczne implikacje. Splątanie stanowi bowiem teoretyczną podstawę kwantowego Internetu przyszłości, superbezpiecznej komunikacji pomiędzy maszynami, do których nikt nie będzie mógł się włamać - komputerami kwantowymi.
Szybki, ale zimny
Za początek idei komputera kwantowego często uznaje się myśl rzuconą przez noblistę Richarda Feynmana w 1981 r. Kolejne podejścia i próby doprowadziły do stworzenia w 2010 r. najbardziej znanego przykładu komputera kwantowego - D-Wave. Wprawdzie niektórzy powątpiewają, czy to „prawdziwy” komputer kwantowy (o tym później), ale liczbowo jego możliwości wyglądają imponująco. Zbudowana niedawno, w 2013 r., kolejna jego wersja, D-Wave 2X, znajdująca się w Centrum Badawczym NASA w Mountain View, w Kalifornii, dowiodła pod koniec 2015 r., iż jest sto milionów razy szybsza niż tradycyjny chip komputerowy.
Dla ostudzenia entuzjazmu trzeba jednak dodać, że porównanie przeprowadzono za pomocą tego, co się da porównać z komputerem kwantowym, czyli symulacji kwantowych działań wykonywanych za pomocą konwencjonalnego procesora. Porównywanie standardowych obliczeń dokonywanych za pomocą zwykłego chipa z typową pracą układu D-Wave nie miałoby sensu. Zasada działania operacji opartych na kubitach informacji jest bowiem całkowicie odmienna od przetwarzania bitowego w komputerach, jakie znamy. D-Wave 2X jest sto milionów razy szybszy w pracy, do której został stworzony, niż tradycyjny komputer w tej samej pracy.
Sygnalizuje to pewien problem, który mamy z komputerami kwantowymi. Mianowicie nie jest jeszcze do końca jasne, jakie pytania mielibyśmy im zadawać i jakie zadania im stawiać. W każdym razie w zadaniach takich, jakie stawiamy tradycyjnym maszynom obliczeniowym, komputery kwantowe nie muszą być lepsze.
D-Wave miał architekturę 128-kubitową i w ciągu dwóch kolejnych lat zdołał podwoić swoją moc obliczeniową, co jest tempem szybszym, niż to zakładane przez słynne prawo Moore’a. D-Wave 2X dysponuje już architekturą 512-kubitową. Niestety, aby popisywać się takimi obliczeniami, kwantowy procesor potrzebuje specyficznych i dość ekstremalnych warunków:
- temperatury ok. 0,02 K;
- prawie doskonałej próżni, czyli środowiska o ciśnieniu 10 mld mniejszym niż atmosferyczne;
- potężnej osłony chroniącej procesor przed polem magnetycznym Ziemi.
Opanować dekoherencję
Aby zrozumieć magiczny świat, w którym funkcjonują kwantowe „chipy”, trzeba zawiesić na chwilę tzw. zdrowy rozsądek.
Większość podstawowych cząstek elementarnych może istnieć w więcej niż jednym stanie. Elektrony np. mają właściwość nazywaną spinem, krętem - choć nie jest to dokładnie to samo, co rozumiemy pod pojęciem obrotu - który może mieć orientację w górę lub w dół. Spin może być mierzony za pomocą wyrafinowanych instrumentów i można nim również sterować. Skierowanie wiązki laserowej o właściwej długości fali w kierunku elektronu z wiązki laserowej powoduje zmianę spinu.
Dziwnie zaczyna się robić jednak, gdy potraktujemy elektron laserem tylko przez połowę czasu potrzebnego do zmiany kierunku wirowania. W takiej sytuacji elektron wchodzi w stan, który fizycy nazywają stanem superpozycji. Mówiąc najprościej, oznacza to, że cząstka ma zarówno spin górny jak i dolny. Jeszcze bardziej dziwne jest to, że pozostaje w tym stanie tylko wtedy, gdy nie jest obserwowana. Jeśli spróbujemy zmierzyć spin, następuje dekoherencja kwantowa, co oznacza, że jest on górny lub dolny w sposób losowy. Ktoś bardziej sceptyczny mógłby wnioskować, że superpozycja jest więc tylko złudzeniem, ale naukowcy udowodnili bez wątpliwości, że rzeczywiście zachodzi.
Wyjaśnijmy to za pomocą tradycyjnego model obliczeń komputerowych, w których każdy bit informacji składa się z cyfr binarnych 0 i 1. System musi standardowo zawierać liczby będące jednym lub drugim. Jednakże w przypadku komputerów kwantowych, tak się nie dzieje. Jeśli umieścimy go w stanie superpozycji, bit ów stanowi zarówno 0, jak i 1, jednocześnie. Możemy rozszerzyć to do umiejscowienia pamięci z kilku bitów. Jeśli wykorzystamy osiem bitów, tak jak to miało miejsce na początku ery mikroprocesorów, to możemy zapisać dowolną liczbę binarną od 00000000 do 11111111, co równe jest skali od 0 do 255 w systemie dziesiętnym. Jednak gdy wszystkie osiem bitów znajduje się w stanie superpozycji, zasób pamięci będzie zawierać wszystkie wartości od 0 do 255 jednocześnie. Co więcej, jeśli przeprowadzamy obliczenia z użyciem zawartości tej pamięci, zachodzi ono na wszystkich tych wartościach na raz. Daje to 256-krotne przyspieszenie w porównaniu z konwencjonalnym komputerem.
Jeśli dojdziemy do 64 bitów, czyli tylu, ile w dzisiejszych procesorach, to uzyskujemy prawie 20 tys. biliardów (20 milionów bilionów) operacji, które mogą być wykonane jednocześnie. Bity, które są w stanie funkcjonować w tak niekonwencjonalny sposób, nazywa się kubitami - co jest przyjętym skrótem dla bitów kwantowych.
Zgodnie ze wspomnianą dekoherencją, gdy próbujemy odczytać wynik wszystkich tych obliczeń, stan superpozycji się zapada, a wynik tego kolapsu pozostaje losowy. To nie oznacza, że się nie da niczego ustalić, chociaż zmusza do zastosowania sprytnych wybiegów, które pozwolą uzyskiwać użyteczne wyniki. Cały trik polega na zastosowaniu algorytmu, który ujawni jedną odpowiedź, mimo zachodzącej dekoherencji. Kubit może być w stanie nierównej superpozycji, czyli np. w sytuacji o większym odsetku zer niż jedynek. Zaczynamy nasze obliczenia z, powiedzmy, wejściem o liczbie ośmiu kubitów, będących w stanie równej superpozycji wszystkich liczb od 0 do 255, a następnie wykonujemy operacje, które dotyczą każdej z nich w ten sam sposób. Jednakże liczby te nie muszą przebywać w równych sobie stanach superpozycji. Można mieć nadzieję, że jest to rozwiązanie, jednak efekt końcowy pozostaje zawsze, do pewnego stopnia, losowy. Najważniejsze jest więc takie zaprojektowanie algorytmu kwantowego, aby było bardzo prawdopodobne, że uzyskujemy w wyniku odpowiednią liczbę.
Najniższy punkt w krajobrazie
System D-Wave 2X korzysta wprawdzie z superpozycji, ale nie jest kwantowym odpowiednikiem dzisiejszych komputerów klasy PC. To adiabatyczny komputer kwantowy, wykorzystujący technikę zwaną wyżarzaniem kwantowym, która jest znacznie łatwiejsza do skalowania. Nie jest to komputer kwantowy „ogólnego przeznaczenia”, ale urządzenie mające na celu rozwiązanie szczególnego typu problemu określanego jako „optymalizacja.” Może być stosowane do nauczania maszynowego, systemów sztucznej inteligencji i do rozwiązywania problemów znanych z biologii, takich jak skręcanie białek.
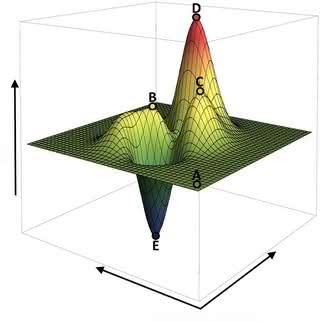
Specjaliści porównują rodzaje problemów optymalizacyjnych, z którymi mierzą się adiabatyczne komputery kwantowe do znajdowania najniższych punktów w matematycznych funkcjach, które można przedstawić jako krajobraz. W przeciwieństwie do fizycznego terenu, krajobraz ten może mieć więcej niż dwa wymiary, co czyni próby znalezienia kombinacji wszystkich zmiennych niezwykle czasochłonne.
W D-Wave 2X kubity funkcjonują w połączonej wzajemnie sieci. Jeżeli każdy z kubitów znajduje się w stanie superpozycji, to możliwa jest i obecna w danym momencie każda permutacja układu, także ta optymalna. Wykorzystując inny osobliwy kwantowy efekt, zwany „tunelowaniem”, w którym cząstki mogą pojawić się po drugiej stronie bariery bez przechodzenia przez nią, system automatycznie integruje się na najniższym stanie energetycznym, na zasadzie - jak to się ujmuje - „przesączania się do rozwiązania o najniższej energii .” Gdy kubity są w końcu odczytywane, pokazują wartości wynikające z owego najmniej energetycznego stanu, który odpowiada najniższemu punktowi „funkcji krajobrazowej” i stanowi odpowiedź na zadane komputerowi pytanie.
Jakakolwiek interakcja ze światem zewnętrznym powoduje utratę superpozycji, dlatego właśnie układ musi być otoczony środowiskiem ochronnym, czyli wieloma warstwami ekranującymi i próżnią. Musi też zejść do bardzo niskich temperatur, ponieważ chip znajduje się na powierzchni, której atomy są rozkołysane.
Społeczność akademicka przyjęła architekturę D-Wave z mieszanymi uczuciami, a eksperci są podzieleni co do tego, czy jest ona rzeczywiście znacząco szybsza niż konwencjonalny komputer i czy są w niej w ogóle wykorzystywane efekty kwantowe. Co więcej, ponieważ maszyna działa w sposób całkowicie inny niż współczesne komputery, nie jest łatwo określić rzeczywistą szybkość D-Wave - dlatego np. że tradycyjnie stosowane miary, takie jak liczba wykonywanych instrukcji, nie mają znaczenia. Mimo to, przechodząc o jedną generację wyżej, ze 128-kubitowego D-Wave do 512-kubitowego D-Wave Two, budowniczowie głoszą przyspieszenie obliczeń o 300 tys. razy. Następne pokolenie będzie mogło pochwalić się 1024 kubitami.
Wielkie liczby i egzoplanety
W końcu istnieje też problem zastosowania komputerów kwantowych. Wielu ekspertów zwraca uwagę, że tak naprawdę musimy stworzyć nie tylko owe urządzenia, ale również problemy, do których będzie sens je stosować. Najbardziej znanym polem wykorzystania są na razie obliczenia na dużych liczbach. Komputerom kwantowym idzie to znacznie szybciej niż konwencjonalnym maszynom. Problem jest ważny dla wojska i służb specjalnych, bo jeśli można rozłożyć na czynniki pierwsze duże liczby, to można złamać także najbezpieczniejsze z bezpiecznych zaszyfrowanych wiadomości.
Inna klasa to tzw. problemy komiwojażera, polegające na znalezieniu najkrótszej drogi pomiędzy kilkoma miastami. Jest to ćwiczenie z gatunku powtarzających się prób i błędów, do którego można zaprząc tradycyjne komputery. Przy kilku miastach wydaje się stosunkowo łatwe, jednak gdy rośnie liczba punktów na mapie, staje się o wiele trudniejsze. To rodzaj zadania, do którego został zaprojektowany D-Wave 2X. NASA może wykorzystywać tę technikę do planowania tras łazików marsjańskich. Agencja kosmiczna zamierza też używać swojego D-Wave 2X do poszukiwania podobnych do Ziemi egzoplanet, na których istnieć mogłoby inteligentne życie. Wykrywać ma je wprawdzie kosmiczny Teleskop Keplera, ale ilość danych do analizy, które on dostarcza, jest ogromna - i właśnie tu mogłaby pomóc informatyka kwantowa.
Technologia wyszukiwawcza Google’a jest dziś wszechobecna, jednak informatyka kwantowa mogłaby ją radykalnie zmienić. Obecnie wyszukiwarki są w stanie dostarczać informacji z danych tekstowych - tymczasem rozpoznawanie obiektów z ogromnego zasobu zdjęć w sieci nie jest jeszcze możliwe. Można spodziewać się, że w przyszłości, dzięki informatyce kwantowej, odbywałoby się to łatwo i skutecznie.
Standardowe komputery pozwalają naukowcom dowiedzieć się więcej na temat fizyki klasycznej. Uważa się, że komputery kwantowe znacznie lepiej sprawdzą się w analizie fizyki kwantowej. Brzmi to może trochę jak masło maślane, ale zdaniu, że „lepsze zrozumienie fizyki kwantowej umożliwi budowę lepszych komputerów kwantowych” - po prostu trudno zaprzeczyć.