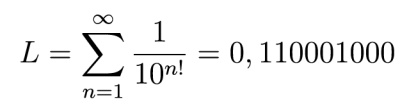Czy coś, czego nie da się policzyć, istnieje? Większość liczb rzeczywistych jest nieznana - nawet matematykom

Liczby wymierne można przedstawić za pomocą ułamka zwykłego. Pozostałe liczby na osi liczbowej to liczby niewymierne. W ich zbiorze również wyodrębnia się różne kategorie, a większości z nich nie potrafimy sobie nawet wyobrazić. Są trudne lub niemożliwe do dokładnego zapisania liczby nieskończenie wielkie, nieskończenie małe, urojone lub inne nietypowe przestrzenie liczbowe.
Te, które da się skonstruować i te, których się nie da
Przykładową liczbą niewymierną jest np. pierwiastek kwadratowy z 2, którego reprezentacja dziesiętna jest nieskończona i nie wchodzi w żaden znany okres. Przy czym √2 można skonstruować, czyli można wygenerować geometrycznie za pomocą cyrkla i linijki, rysując trójkąt prostokątny o dwóch bokach o długości jednej jednostki. Przeciwprostokątna tego trójkąta ma wtedy długość √2. W podobny sposób geometrycznie da się skonstruować także złotą proporcję Φ i wiele innych wartości niewymiernych.
Jednak nawet w starożytności ludzie znali liczby, których nie można było przedstawić w tak prosty, geometryczny sposób. Znanym przykładem jest podwojenie sześcianu. W jaki sposób sześcian o boku długości 1 można przekształcić w sześcian o dwukrotnie większej objętości? Jak orzekł w 1837 roku matematyk Pierre Wantzel, długości krawędzi ∛2 wymaganej dla takiego podwojonego sześcianu nie można skonstruować za pomocą linijki. Jednak ∛2 należy wciąż do liczb algebraicznych, które można zapisać jako rozwiązanie równania wielomianowego. Dla ∛2 odpowiednim równaniem jest x3=2.
Nie ma prostego wzoru, za pomocą którego można obliczyć takie „transcendentalne” lub przestępne liczby. Podaje się, że pierwszą znaną liczbą tego typu była liczba Liouville’a (1), choć do tej kategorii zaliczana jest znana znacznie dawniej liczba π (2). Jeszcze grecki matematyk Archimedes znalazł regułę obliczania π w przybliżeniu. Dziś istnieje wiele algorytmów, które potrafią obliczyć ją do prawie sześciuset milionów miejsc po przecinku. Dysponując wystarczającą mocą obliczeniową i czasem, liczbę tę można wyznaczyć z dowolną dokładnością, przynajmniej w teorii. Jednak wciąż nie będzie obliczona „do końca”. To samo dotyczy liczby Eulera (e), czyli 2√2.
Chociaż istnieją metody pozwalające stwierdzić, czy liczba jest konstruowalna, trudno jest udowodnić, czy dana wartość jest przestępna, czyli nie należy do liczb algebraicznych. Na przykład w 1934 roku radziecki matematyk Aleksander Gelfond udowodnił, że liczba zespolona eπ jest przestępna. Jednak to, czy wartości πe, π × e lub π – e są algebraiczne czy przestępne, do dziś pozostaje niejasne.
Turing i wkroczenie do świata nieobliczalności
Do XX wieku ludzie zakładali, że liczby przestępne są najbardziej egzotyczną rzeczą, na jaką możemy natrafić w zbiorze liczb rzeczywistych. Jednak w 1937 roku brytyjski matematyk Alan Turing (3) opublikował artykuł na temat czegoś jeszcze „dzikszego”, mianowicie zagadnienia obliczalności liczb. Użył tego terminu do opisania wszystkich wartości, dla których istnieje reguła obliczeniowa (czyli algorytm), którą komputer może wykonać, aby obliczyć wartość liczbową z dowolnym stopniem dokładności.
Prawie wszystkie znane liczby przestępne, np. π i e, należą z tego punktu widzenia do kategorii obliczalnych. W końcu znamy sposoby (algorytmy) obliczania ich przynajmniej przybliżonej wartości liczbowej. Jak wykazał Turing w swojej pracy, istnieją jednak też liczby nieobliczalne, czyli takie, których wartości nie mogą być przybliżone z dowolną precyzją. To znaczy, że nie mamy pojęcia, jaką mają wartość, nawet w przybliżeniu.
Można to spróbować wyjaśnić w możliwie prosty sposób (w tym artykule nie wchodzimy w gąszcze równań), nawiązując do nieskończonych rozmiarów różnych zbiorów liczbowych, którymi pierwszy zajął się Georg Cantor w XIX wieku, wykazując na przykład, że zbiór liczb naturalnych, całkowitych i wymiernych ma tę samą kardynalność (moc zbioru). Jak wykazał Cantor, kardynalność liczb naturalnych jest najmniejszą możliwą nieskończonością. Nazwał ją „policzalnie nieskończoną”. Liczb rzeczywistych nie można policzyć. Cantor dowodził, że kardynalność liczb rzeczywistych jest z konieczności większa niż liczb naturalnych. Liczby rzeczywiste tworzą zatem zbiór niepoliczalny.
Jak jednak stwierdził Turing, wszystkie liczby obliczalne muszą być policzalne w rozumieniu Cantora. Dla każdej z nich można opracować maszynę, która po prostu oblicza jej wartość. Ponieważ można ponumerować maszyny liczące te liczby, liczby obliczalne są z konieczności policzalne. Nieformalnie możemy myśleć o liczbie obliczalnej tak, jak zrobił to Marvin Minsky, jeden z ojców AI, a mianowicie jako o „liczbie, dla której istnieje maszyna Turinga, która, biorąc pod uwagę n na jej początkowej taśmie, kończy się n-tą cyfrą tej liczby (zakodowaną na jej taśmie)”.
Z drugiej strony prowadzi to do sytuacji, w której liczby niepoliczalne, dla których nie można zbudować maszyny obliczającej, stanowią większość liczb rzeczywistych – jest ich niepoliczalna liczba. Liczby nieobliczalnych znamy niewiele. Niektóre znane przykłady liczb nieobliczalnych zostały zdefiniowana przez znany z informatyki problem zatrzymania (haltingu), opracowany przez Turinga. Opisuje się je przez sytuację, w której komputer wykonujący określony zestaw instrukcji w celu rozwiązania problemu (innymi słowy, komputer używający algorytmu) zatrzymuje się w pewnym momencie, zamiast kontynuować obliczenia w nieskończoność. Jak udowodnił Turing, chociaż taka maszyna mogłaby ocenić, czy niektóre algorytmy mogą być wykonywane w skończonym czasie, nie istnieje żadna metoda, która mogłaby to zrobić dla wszystkich możliwych kodów programowania.
Inaczej to ujmując, według Turinga liczba rzeczywista, dla której istnieje algorytm, mechaniczna procedura obliczania jej wartości z dowolną dokładnością, z coraz większą precyzją, jest obliczalna. Zatem na przykład π jest obliczalną liczbą rzeczywistą, √2 jest obliczalną liczbą rzeczywistą, a także e jest obliczalną liczbą rzeczywistą. Zbiór obliczalnych liczb rzeczywistych jest tak liczny jak metody obliczania, algorytmy, programy komputerowe. A programów komputerowych jest najwyżej tyle, ile liczb całkowitych1, 2, 3, 4, 5, ... – można myśleć o programie komputerowym jak o bardzo dużej liczbie całkowitej.
Problem haltingu jest bezpośrednim zastosowaniem twierdzenia o niekompletności innego wybitnego matematyka, Kurta Gödla, które, najogólniej to wyjaśniając, mówi, że nie wszystkie twierdzenia matematyczne można udowodnić. Twierdzenie o niekompletności Gödla z 1931 roku mówi, że jeśli wziąć pod uwagę dowolny skończony zestaw aksjomatów, będą istniały prawdziwe twierdzenia matematyczne, które wymykają się z tego systemu, ale nie można ich udowodnić na podstawie tych aksjomatów.
Argentyńsko-amerykański matematyk Gregory Chaitin w 1975 roku zaproponował liczbę rzeczywistą, która nie jest obliczalna, obecnie nazywaną stałą Chaitina, omega (Ω). Reprezentuje ona prawdopodobieństwo, że losowo skonstruowany program zatrzyma się/zakończy. Załóżmy, że uruchamiamy uniwersalną maszynę Turinga na losowym programie binarnym. W szczególności, za każdym razem, gdy wymagany jest kolejny bit programu, rzucamy monetą i podajemy binarne wyjście do maszyny. Jakie jest prawdopodobieństwo, że maszyna Turinga się zatrzyma? Eksperyment myślowy Chaitina jest prototypowym przykładem problemu zatrzymania. Problem haltingu to problem polegający na określeniu, na podstawie opisu dowolnego programu komputerowego i danych wejściowych, czy program zakończy działanie (zatrzyma się), czy będzie działał w nieskończoność. Aby dokładnie obliczyć stałą Chaitina, trzeba by wiedzieć, które programy zatrzymują się, a które nie, co nie jest możliwe, zgodnie z problemem haltingu. W 2000 roku matematykowi Cristianowi S. Calude i jego kolegom udało się obliczyć pierwsze cyfry stałej Chaitina: 0,0157499939956247687... Oznacza to, że jeśli losowo wygenerujemy program w języku używanym przez Caludea i jego współpracowników, będzie on działał (zatrzymywał się) z prawdopodobieństwem około 1,58 proc. w skończonym czasie działania. Nawet jeśli wynik ma wysoką dokładność, stała Chaitina nie może być obliczona z dowolną precyzją.
Istnieją inne skomplikowane metody definiowania liczb nieobliczalnych. Mimo to, biorąc pod uwagę obfitość liczb obliczalnych, które znamy, zawsze zaskakujące jest to, że wartości nieobliczalne dominują w zbiorze liczb rzeczywistych.
Zniszczone marzenia o pewnikach
Współczesne badania nad obliczalnością rozpoczęły się około 1900 roku wraz z ogłoszeniem programu Hilberta, mającego na celu aksjomatyzację podstaw matematyki. Stało się to po tym, jak sam Hilbert pokazał w 1899 roku, że spójność geometrii sprowadza się do spójności liczb rzeczywistych. Program Hilberta (1904) został zatem ustanowiony, aby spróbować podobnie wykorzystać skończoność dowodów matematycznych, aby pokazać, że nie można wyprowadzić sprzeczności. Gdyby taki fundament mógł zostać ustanowiony, dowody matematyczne byłyby całkowicie wyrażalne w kategoriach symboli logicznych. Gdyby udało się to osiągnąć, wszystkie dowody, w tym m.in. dowody ostatniego twierdzenia Fermata, hipotezy Riemanna i przypuszczenia Poincarégo, byłyby nieuniknionymi konsekwencjami systemu matematycznego, w którym są wyrażone. I w końcu, jeśli taki „program” zostałby zrealizowany, to można by zbudować wystarczająco sprawną maszynę, pozwolić jej działać wystarczająco długo, aby ostatecznie wszystkie twierdzenia matematyczne zostały ujawnione.
Niecałe 30 lat później wspomniany Kurt Gödel (1906–1978) opublikował pracę „Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I”, w której zawarł „twierdzenie VI” niszczące marzenie Hilberta o w pełni zaksjomatyzowanym, niepodważanym fundamencie matematyki. Gödel pokazał, że jakikolwiek system będziemy konstruować, nieważne jak solidny, zawsze będzie z natury niekompletny. Zawsze będą istniały stwierdzenia wyrażalne w systemie, których nie da się udowodnić, biorąc pod uwagę jego aksjomaty (pewniki).
Czy nieobliczalne/nieopisywalne liczby rzeczywiste „istnieją”? To pytanie o charakterze filozoficznym. Np. zwolennik szkoły platońskiej powie, że istnieją, nawet jeśli nie mamy możliwości, by je skonstruować. Finitysta (jest taki kierunek w „filozofii matematyki”) może powiedzieć, że nie istnieją, dlatego że nie mamy algorytmu do obliczenia lub nawet rozpoznania takiej liczby. Zatem odpowiedź na pytanie – co wynika z tego, że zdecydowanej większości liczb rzeczywistych nie da się obliczyć – zależy od filozofii. I taka może być niespodziewana pointa rozważań o obliczalności liczb.
Mirosław Usidus