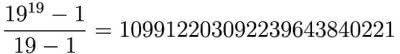Kiedy rano jadę dziewiętnastką…

Tytuł odcinka jest niedokładnym tytułem piosenki sprzed dosłownie siedemdziesięciu lat. W tej piosence jechało się do pracy tramwajem linii 18, a wokół było widać odbudowującą się Warszawę. Ale ja mam sentymentalny stosunek właśnie do tramwaju linii 19. Ilekroć jestem w mieście z tramwajami, staram się przejechać tą linią choćby kilka przystanków. Dlaczego? A, tak jakoś…

Ucieszyłem się zatem z zaproszenia na 19. Konferencję Naukową Dydaktyków Matematyki, organizowaną tradycyjnie przez Uniwersytet Szczeciński w Pobierowie nad Bałtykiem.

Oglądałem wieczorem w telewizji programy informacyjne, a o dziesiątej wieczorem znany program, który chce uchodzić za satyryczny. W tym ostatnim najpierw było trochę frazesów o matematyce – Królowej Nauk, potem kilka rozmów z uczniami. Niestety, potem jeden z prowadzących chciał zrobić dobre wrażenie na widzach i zaczął chwalić się, jakim to był „głąbem” z matematyki. Nie on pierwszy, nie ostatni. „Wielomian” był dla niego kimś, kto ma kilka nazwisk, a słowa „planimetria” nie rozumiał. Trudno zrozumieć, dlaczego wypada się popisywać nieznajomością matematyki. „Nie wiesz, co to sinus – no to jesteś swój chłop, szczera dusza”. Na nieznajomość matematyki snobował się – trudno to inaczej określić – nawet i Julian Tuwim, którego poezję słusznie oceniamy bardzo wysoko.

***

Tyle mojej prywatnej publicystyki. Przejdźmy do matematyki. Na wspomnianej konferencji w Pobierowie wygłosiłem zatem referat o liczbie 19. Pasuje do tego odcinka „Rozmaitości Matematycznych”. Sądzę przecież, że większość Czytelników jest w wakacyjnym nastroju i jeżeli sięgnie po coś do czytania, to nie po trudne teorie naukowe, a po coś lekkiego w treści i formie. Chociaż… kolorowe i efektowne rysunki skrywają nie-kiedy coś znacznie ważniejszego.

Na plakacie konferencji dziewiętnastka została napisana znakami rzymskimi: XIX. Ten sposób zapisu liczb jest w zaniku. Jeszcze tylko stulecia się tak zapisuje. Niekiedy pozwalam sobie na żart i w formularzu wpisuję dzień i miesiąc swojego urodzenia tak, jak mnie nauczano dawno temu w szkole: 5 IV (czyli piąty kwietnia). Mogę tak się bawić tylko w wersji
papierowej formularza.

Zapis XIX, traktowany jak figura geometryczna, jest symetryczny zarówno w pionie, jak i w poziomie. Jest tylko siedem liczb o tej własności: I, II, III, V, XIX, XX, XXX. Potem nie ma już żadnych!

W arytmetyce liczba 19 nie wyróżnia się szczególnie. Interesująca, choć zupełnie bezużyteczna, jest cecha podzielności przez 19: liczba 100a+b jest podzielna przez 19, gdy a+4b d zieli się p rzez 1 9. Sprawdźmy na przykładzie:
19∙1234=23446→234+4∙46=418→4+72=76=4∙19

Ciekawie wyglądałoby „wykazanie” tym sposobem zupełnie oczywistego faktu, że 190 dzieli się przez 19. Polecam, a dlaczego „wykazanie” wziąłem w cudzysłów, okaże się natychmiast.

***

Choć w związku z kryptografią poszukiwanie wielkich liczb pierwszych ma duże znaczenie, to na pewno tylko ciekawostką jest to, że liczba będąca naprzemienną sumą silni liczb od 1 do 19

19!−18!+17!−16!+15!−14!+13!−12!+11!−10!+9!−8! +7!−6!+5!−4!+3!−2!+1!=115578717622022981 jest liczbą pierwszą. Suma naprzemienna to – jak łatwo się domyślić – wyrażenie, gdzie na przemian stawiamy plusy i minusy.

Zostańmy jeszcze na chwilę przy liczbach pierwszych. Mamy

i jest to liczba pierwsza. Innymi liczbami n, że jest liczbą pierwszą, są tylko 2, 3, 7, 31.

W 1770 roku brytyjski matematyk Edward Waring postawił hipotezę, że każda liczba da się przedstawić w postaci odpowiedniej liczby n potęg. W 1909 roku David Hilbert wykazał, że tak istotnie jest. W 1986 roku trzech matematyków, z których pierwszy i trzeci mają ciekawe nazwiska: Balasubramanian, Deshouillers i Dress, wykazali, że dla n=4 tą „odpowiednią” liczbą jest 19. To znaczy, że każda liczba może być wyrażona jako suma co najwyżej dziewiętnastu liczb postaci k⁴. Zagadnienie znalezienia „odpowiedniej” liczby dla danego wykładnika n jest dalekie od ogólnego rozwiązania.

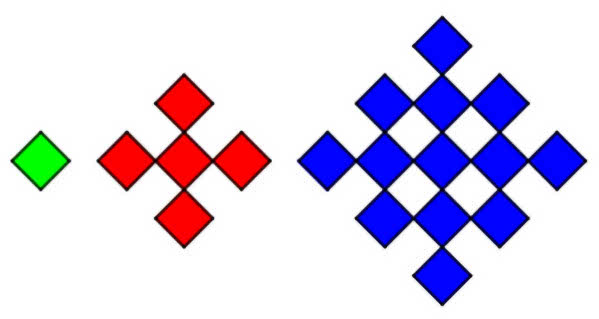
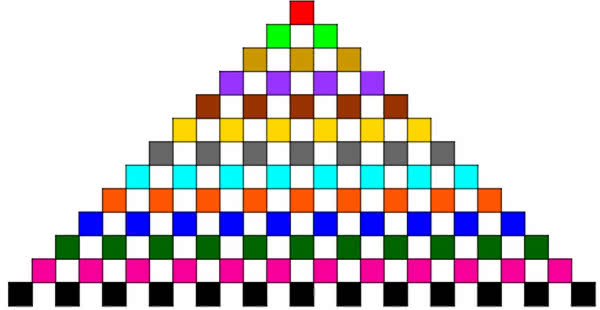
Bardziej poglądowa jest geometria. Na rysunku 1 mamy tak zwane liczby środkowo-kwadratowe. Po prostu ustawiamy małe kwadraciki w haftowaną serwetkę. Następnymi takimi liczbami będą 25, 41, 65, 85, 113, …, 1985, …, 4513 i tak dalej bez końca. Dodając je, otrzymujemy tak zwane liczby latawcowe. Skąd taka nazwa? Wystarczy spojrzeć na rysunek 1.

Rysunek 1.

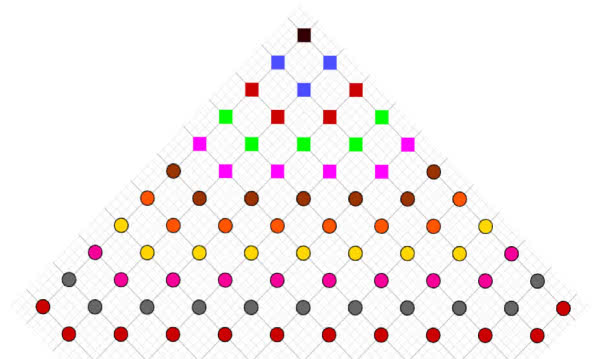
Liczba 19 pojawia się i w dywaniku na rysunku 2. Ile jest punktów zaznaczonych kwadracikami (nie kółkami)? Właśnie 19.

Rysunek 2.

Już Platon wiedział, że jest tylko pięć brył foremnych: czworościan, sześcian, ośmiościan, dwunastościan i dwudziestościan. Ośmiościan ma osiem ścian trójkątnych. Można go zbudować z dziewiętnastu piłeczek pingpongowych. Na rysunku 3 mamy widok od góry: wierzchołek, cztery piłeczki w następnej warstwie, dziewięć w środkowej. Niewidoczna jest kolejna warstwa
z czterech kulek i pojedynczy wierzchołek.

Rysunek 3.

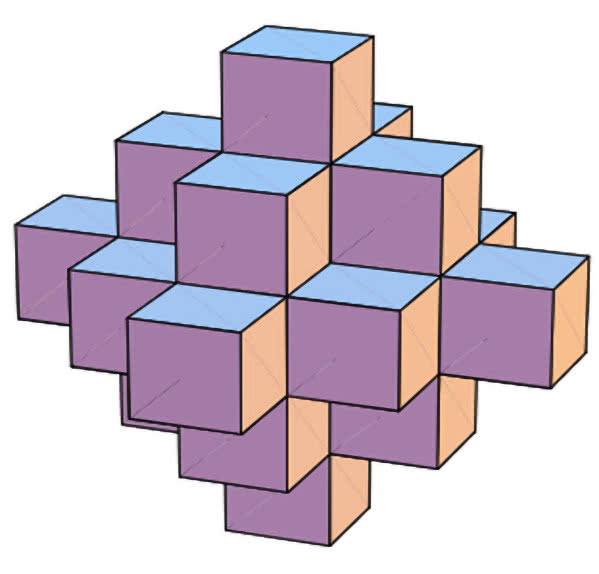
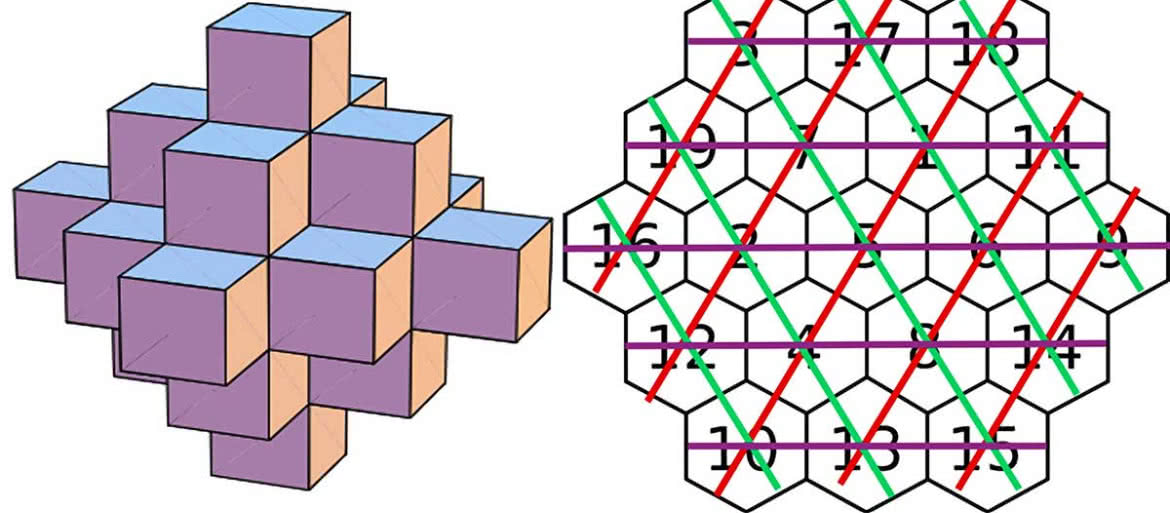
Rysunek następny pokazuje inne ustawienie dziewiętnastu sześcianików w ciekawy krzyż przestrzenny.

Rysunek 4.

Oficerowie armii francuskiej w XIX wieku często zajmowali się amatorsko (a niekiedy półzawodowo) matematyką. Mamy w geometrii nawet twierdzenie Napoleona. Pierwszy inwersor (urządzenie zamieniające ruch obrotowy na prostoliniowy) wynalazł 1864 roku oficer marynarki Charles-Nicolas Peaucellier. Oficerem artylerii był Gaspar Monge, uważany za twórcę geometrii wykreślnej.

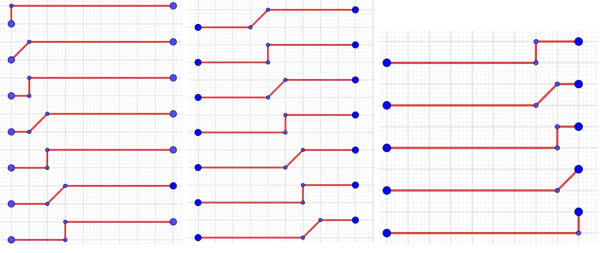
Rysunek 5. Gdzie można zobaczyć liczbę 19? Wskazówka: porównaj z rysunkiem 2

Jednym z takich amatorów był Henri August Dellanoy (1833–1915). Jego imieniem nazywamy dziś liczby, które pokazują, ile dróg wiedzie od jednego punktu do drugiego. Konkretnie: takie drogi między punktami siatki prostokątnej, które biegną na północ, wschód albo północny wschód (czyli po przekątnej kratki). Na rysunku 6 widzimy drogi od lewego dolnego do prawego górnego punktu. Jest ich właśnie 19. Przypomina to drukowane obwody elektryczne, chociaż ta analogia jest trochę naciągana. Podobno liczby Dellanoy mają zastosowanie w robotyce. Piszę „podobno”, bo jestem już poza przednią linią swoich wiadomości. Ale zgodziłbym się z tym – liczby Dellanoy mogą pokazać, na ile sposobów robot może wykonać pewne zadanie. W dydaktyce matematyki przydają się do nauki pisania prostych programów rekurencyjnych. Polecam Czytelnikom zmuszenie chatGPT do napisania takiego programu.

Rysunek 6.

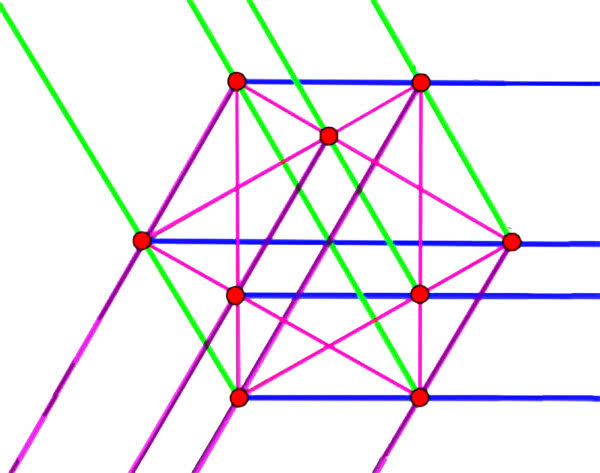
Bardziej poważnej matematyki dotyka rysunek 7, chociaż sformułowanie zadania wcale tego nie sugeruje. Matematycy lubią bowiem niecodzienną interpretację swoich twierdzeń. Jednym z najlepszych przykładów jest twierdzenie z trudnej dyscypliny matematycznej, zwanej analizą funkcjonalną, tak zwane „twierdzenie o kanapkach”: bułkę z masłem i szynką można przekroić jednym płaskim cięciem tak, by jednocześnie przepołowić bułkę, masło i szynkę. W gastronomii to twierdzenie na pewno jest bezużyteczne. Na rysunku 6 mamy natomiast rozwiązanie jednego z zadań z obszernego tematu „sadzenie drzew w sadzie”. Jak posadzić (jeśli w ogóle da się) n drzew w k rzędach po m drzew w każdym? Na tym rysunku
mamy n=1, k=19, m=3, czyli 12 drzew w 19 rzędach, po 3 w każdym rzędzie.

Rysunek 7. 12 drzew w 19 rzędach, po 3 w każdym

Uważny Czytelnik może policzy punkty i proste na rysunku 7… i wyjdzie mu to inaczej, a mianowicie 9 punktów i 11 prostych. Gdzie reszta?

Odpowiedź jest doprawdy matematyczna: w nieskończoności. Nieskończoność nie jest trudnym pojęciem geometrii rzutowej, czyli geometrii perspektywy zbieżnej. Każdy bowiem wie, że proste równoległe (na przykład szyny kolejowe) zbiegają się w jednym punkcie – na horyzoncie. Z malarskiego punktu widzenia linia w nieskończoności to po prostu horyzont. Punkty na horyzoncie to punkty, w których zbiegają się proste równoległe. Każdy punkt odpowiada określonemu kierunkowi. Na rysunku 7 mamy trzy punkty w nieskończoności, odpowiadające trzem kierunkom prostych równoległych. Brakująca dziewiętnasta prosta to prosta nieskończoności – nasz horyzont.

Na uprawach się nie znam. Wyobrażam sobie jednak, że takie zagadnienia nie zaprzątają umysłu sadowników. Gdyby jednak, to czy plan posadzenia drzewek jest wykonalny? Przecież nie możemy sadzić w nieskończoności! Otóż możemy. Wystarczy sobie przyjąć, że nasza nieskończoność, nasz horyzont, jest odległy od nas nie o kilometry, tylko o… metry, a może lepiej: o dziesiątki metrów. Geometrią perspektywy zbieżnej zajmowali się malarze, graficy i matematycy.

***

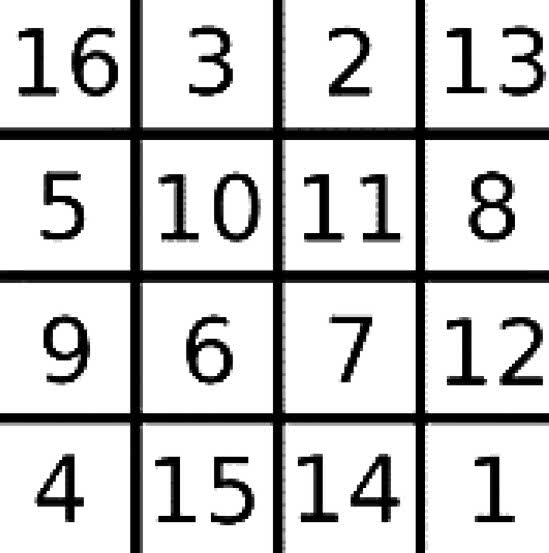
Najbardziej efektowne jest pojawienie się liczby 19 w sześciokącie magicznym. Figury magiczne fascynowały ludzi co najmniej od czasów Renesansu. Były to przeważnie kwadraty, tak wypełnione liczbami, by sumy w kilku kierunkach były takie same. Słynny jest kwadrat Albrechta Dürera (rysunek 8), umieszczony na głęboko symbolicznym obrazie „Melancholia”. Są w tym kwadracie wszystkie liczby od 1 do 16. Dodając liczby w rzędach pionowych, poziomych i po przekątnych, dostajemy zawsze tę samą sumę 34. Dodatkowo, dwie sąsiednie liczby w czwartym rzędzie dają rok powstania dzieła: 1514. Artysta chciał zapewne pokazać tajemną moc takiego talizmanu.

Rysunek 8.

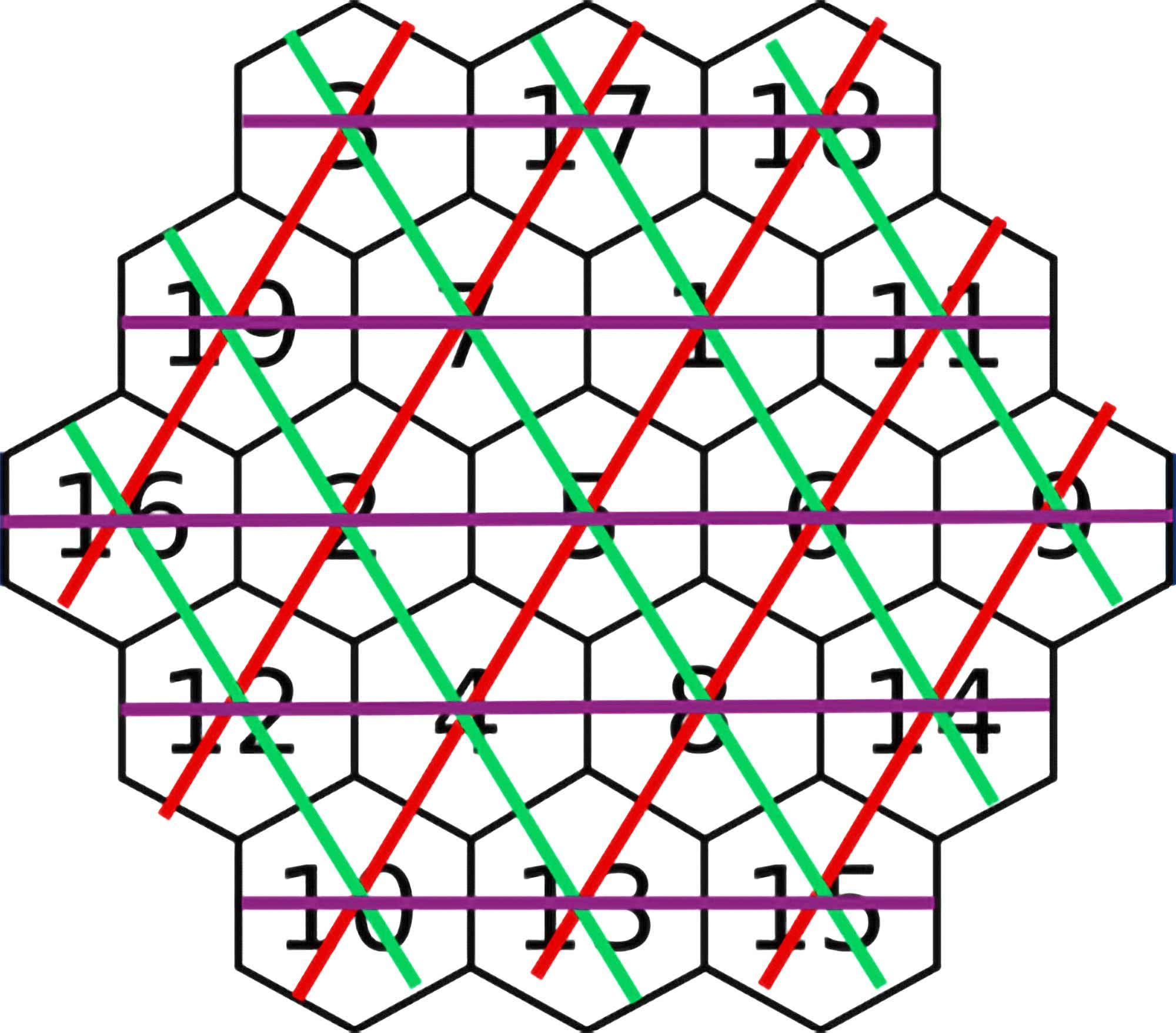
Podobnie jest z sześciokątem magicznym. Jest on unikatowy (rysunek 9). Zawiera wszystkie liczby od 1 do 19, a sumy w każdym kierunku są takie same: 38.

Rysunek 9.

Taka niepozorna liczba, a tyle ma własności! Zastanawiam się od czasu do czasu, czy chciałbym mieć znowu 19 lat. Prawie zawsze myślę, że… nie. Ale to nie jest temat do kącika matematycznego.

Michał Szurek