Wycieczka w nierzeczywisty świat matematyki

Dlaczego tak się bronię? Z prostej przyczyny - jestem w takim wieku, w którym być może przestaje się rozumieć otaczający świat. Może uczę ich, jak zaprzęgać i wyprzęgać konie, a nie jak jeździć samochodem? Może uczę ich, jak pisać gęsim piórem? Mam wprawdzie o osobie lepsze zdanie, uważam, że "nadążam", ale…

Do niedawna w liceum omawiało się liczby zespolone. I właśnie w ową środę przyszedłem zrezygnowany do domu - niemal nikt ze studentów nie nauczył się jeszcze, co to jest i jak się tymi liczbami posługiwać. Kilkoro patrzy na całą matematykę, jak gęś na malowane wrota. Ale również szczerze zdziwili się, gdy powiedziałem, jak się uczyć. Po prostu - każda godzina wykładu to dwie godziny nauki w domu: czytanie podręcznika, wstępna nauka rozwiązywania zadań z danego tematu itp. Tak przygotowani przychodzimy na ćwiczenia, gdzie wszystko doskonalimy… Mili studenci uważali najwyraźniej, że odsiedzenie na wykładzie - najczęściej patrząc w okno - gwarantuje już wejście wiedzy do głowy.

Stop! Dość tego. Opiszę swoją odpowiedź na pytanie, jakie dostałem na zajęciach ze stypendystami Krajowego Funduszu na Rzecz Dzieci - instytucji, która wspiera dzieci zdolne z całego kraju. Pytanie (a raczej propozycja) brzmiało:

"Czy mógłby nam Pan opowiedzieć coś o liczbach nierzeczywistych?"

"Oczywiście", odparłem. 

Rzeczywistość liczb

Po pierwsze. Nie ma pojęcia "liczby nierzeczywistej". To tak, jakby po przeczytaniu artykułu o słoniach poprosić: "a teraz poprosimy o nie-słoniach". Są wprawdzie liczby całkowite i niecałkowite, wymierne i niewymierne, ale nierzeczywistych nie ma. Dokładniej: liczb, które nie są rzeczywiste, nie nazywamy nierzeczywistymi. Typów "liczb" jest w ogóle w matematyce bardzo dużo i różnią się one od siebie wzajemnie jak - pozostańmy przy porównaniu zoologicznym - słoń od dżdżownicy.

Po drugie - będziemy wykonywać operacje, o których być może dowiedzieliście się już, że są zakazane: wyciąganie pierwiastków z liczb ujemnych. Otóż matematyka pokona i takie bariery. Czy to jednak ma sens? W matematyce jest jak w każdej innej nauce: o tym, czy jakaś teoria wejdzie na stałe do skarbnicy wiedzy, decyduje... zastosowanie. Jeżeli jest nieprzydatna, ląduje jeśli nie w śmietniku, to w jakimś lamusie historii wiedzy. Bez liczb, o których opowiadam w końcu artykułu, nie da się rozwijać matematyki. Ale zacznijmy od ciekawostek. Co to są liczby rzeczywiste, wiecie. Wypełniają one oś liczbową gęsto i bez luk. Wiecie też, co to są liczby naturalne: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, ........ - wszystkie one nie zmieszczą się w pamięci nawet największego komputera. Ładnie się też nazywają: naturalne. Mają tyle ciekawych własności. Jak podoba Wam się taka:

1 + 15 + 42 + 98 + 123 + 179 + 206 + 220 = 3 + 11 + 46 + 92 + 129 + 175 + 210 + 218
1² + 15² + 42² + 98² + 123² + 179² + 206² + 220² = 3² + 11² + 46² + 92² + 129² + 175² + 210² + 218²
1³ + 15³ + 42³ + 98³ + 123³ + 179³ + 206³ + 220³ = 3³ + 11³ + 46³ + 92³ + 129³ + 175³ + 210³ + 218³
1⁴ + 15⁴ + 42⁴ + 98⁴ + 123⁴ + 179⁴ + 206⁴ + 220⁴ = 3⁴ + 11⁴ + 46⁴ + 92⁴ + 129⁴ + 175⁴ + 210⁴ + 218⁴
1⁵ + 15⁵ + 42⁵ + 98⁵ + 123⁵ + 179⁵ + 206⁵ + 220⁵ = 3⁵ + 11⁵ + 46⁵ + 92⁵ + 129⁵ + 175⁵ + 210⁵ + 218⁵
1⁶ + 15⁶ + 42⁶ + 98³ + 123⁶ + 179⁶ + 206⁶ + 220⁶ = 3⁶ + 11⁶ + 46⁶ + 92⁶ + 129⁶ + 175⁶ + 210⁶ + 218⁶
1⁷ + 15⁷ + 42⁷ + 98³ + 123⁷ + 179⁷ + 206⁷ + 220⁷ = 3⁷ + 11⁷ + 46⁷ + 92⁷ + 129⁷ + 175⁷ + 210⁷ + 218⁷

"To naturalne interesować się liczbami naturalnymi" powiedział Carl Lindenholm, a Leopold Kronecker (1823-1891) ujął sprawę krótko: "Bóg stworzył liczby naturalne - wszystko inne jest dziełem człowieka!" Ułamki (nazywane przez matematyków liczbami wymiernymi) też mają zadziwiające własności:

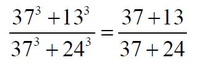
a w równości:

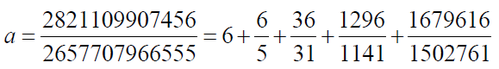
można, zaczynając od lewej strony, ścierać plusy i zastępować je znakami mnożenia - i równość pozostanie prawdziwa:

I tak dalej.
Jak wiecie, na ułamki a/b, gdzie a i b są liczbami całkowitymi i b≠0, mówimy liczby wymierne. Ale tylko po polsku one się tak nazywają. Po angielsku, francusku, niemiecku i rosyjsku mówi się na nie liczby racjonalne. W wersji angielskiej: rational numbers. Liczby niewymierne to irrational, nieracjonalne. Po polsku mówimy też o irracjonalnych teoriach, pomysłach, czynach - to te zwariowane, wydumane, niewytłumaczalne. Kobiety podobno boją się myszy - prawda, jakie to irracjonalne?

W starożytności liczby miały duszę. Każda coś znaczyła, coś symbolizowała, w każdej odbijała się cząstka owej harmonii Wszechświata, czyli po grecku Kosmosu. Samo słowo "kosmos" znaczy właśnie "ład, porządek". Najważniejsze były szóstka (liczba doskonała) i dziesiątka, suma kolejnych liczb 1+2+3+4, złożona z innych liczb, których symboliczność dotrwała do dzisiaj. Pitagoras nauczał więc, że liczby są początkiem i źródłem wszystkiego i dopiero odkrycie liczb niewymiernych sprawiło, że ruch pitagorejski zwrócił się ku geometrii. Znamy ze szkoły rozumowanie, że

√2 jest liczbą niewymierną

Załóżmy bowiem, że jest: i że ułamka tego nie da się już skrócić. W szczególności obie liczby p i q nie są parzyste. Podnieśmy do kwadratu: 2q²=p². Liczba p nie może być nieparzysta, bo wtedy p² też by była, a po lewej stronie równości stoi wielokrotność 2. A więc p jest parzysta, czyli p=2r, a więc p²=4r². Skróćmy równanie 2q²=4r² przez 2. Otrzymamy q²=2r² i widzimy, że q musi być też parzysta, a przyjęliśmy, że tak nie jest. Otrzymana sprzeczność kończy dowód - w każdej książce matematycznej można tę formułę często znaleźć. To dowód nie wprost - ulubiona metoda sofistów.

Tej niewymierności nie mogli pojąć pitagorejczycy. Wszystko powinno było dać się opisać liczbami, a przekątna kwadratu, którą każdy może narysować sobie patykiem na piasku, nie ma żadnej - to znaczy wymiernej - długości. "Daremna była nasza wiara", zdają się mówić pitagorejczycy. Jak to? To jakieś... irracjonalne. Związek próbował ratować się metodami sekciarskimi. Każdy, kto by ośmielił się wyjawić istnienie liczb niewymiernych, miał być karany śmiercią i podobno sam mistrz wykonał pierwszy wyrok.

Ale "myśl uszła cało". Nadszedł złoty wiek. Grecy zwyciężyli Persów (Maraton 490, Plateje 479). Okrzepła demokracja, powstały nowe ośrodki myśli filozoficznej, nowe szkoły. Wyznawców pitagoreizmu wciąż dzieliła trudność związana z liczbami niewymiernymi. Jedni głosili: tej tajemnicy nie zgłębimy; możemy ją tylko kontemplować i zachwycać się Niezbadanym. Drudzy byli bardziej pragmatyczni i nie czuli respektu przed Tajemnicą. Pojawiły się wtedy dwie konstrukcje myślowe, które pozwalały zrozumieć liczby niewymierne. To, że dzisiaj rozumiemy je całkiem nieźle, zawdzięczamy Eudoksosowi (V wiek p.n.e.), a dopiero w końcu XIX wieku matematyk niemiecki Richard Dedekind nadał teorii Eudoksosa należyte opracowanie, zgodnie z wymogami surowej logiki matematycznej.

Waga liczb albo tortury

Czy dałoby się żyć bez liczb? Jeśli nawet, to co to by było za życie... Po buty do sklepu musielibyśmy chodzić z patyczkiem, którym zmierzyliśmy uprzednio długość swojej stopy. "Poproszę jabłek, o, o tyle!" - pokazywalibyśmy sprzedawcy na targu. "Jak daleko jest z Modlina do Nowego Dworu Mazowieckiego"? "Dość blisko!".

Liczby służą do mierzenia. Wyrażamy też nimi wiele innych pojęć. Na przykład skala mapy opisuje, jak bardzo powierzchnia kraju została zmniejszona. Skala "dwa do jednego" czyli po prostu 2, wyraża fakt, że coś zostało powiększone dwukrotnie. Ujmijmy to matematycznie: każdej jednokładności odpowiada pewna liczba - jej skala.

Zadanie. Zrobiliśmy odbitkę kserograficzną, powiększając obraz a razy. Następnie powiększony fragment powiększyliśmy powtórnie b razy. Jaka jest skala łącznego powiększenia? Odpowiedź: a×b, a razy b. Te skale trzeba pomnożyć. Liczba "minus jeden", -1, odpowiada jednokładności, która jest symetrią środkową, czyli obrotem o 180 stopni. A jaka liczba odpowiada obrotowi o 90 stopni? Nie ma takiej liczby. Jest, jest... a raczej zaraz będzie. Jesteście gotowi na tortury umysłu? Bądźcie odważni i wyciągnijcie pierwiastek kwadratowy z "minus jeden". Słucham? Że nie da się? Przecież uprzedzałem, że macie być odważni. Wyciągajcie! Ej, uch, ciągnijcie, ciągnijcie... pomogę... Jest: −1 Skoro już go mamy, to spróbujmy się nim posłużyć... Oczywiście możemy teraz już wyciągać pierwiastki ze wszystkich liczb ujemnych, np.:

√-4 = 2√-1, √-16 = 4√-1

- "nie zważając na tortury umysłu, jakie się z tym wiążą". Tak właśnie napisał w 1539 r. Girolamo Cardano, próbując pokonać trudności myślowe związane z - jak się wkrótce nazwało - wielkościami urojonymi. Rozpatrywał on takie oto…

…Zadanie. Podzielić 10 na dwie części, których iloczyn jest równy 40. Przypominam z poprzedniego odcinka, że pisał mniej więcej tak: To oczywiście niemożliwe. Jednakże zróbmy, co następuje: podzielmy 10 na dwie równe części, każda równa 5. Mnożymy je - dostaliśmy 25. Od otrzymanego 25 odejmij teraz, jeśli łaska, 40, a dostaniesz -15. Teraz patrz: √-15 dodane i odjęte od 5 daje liczby, których iloczyn jest 40. Te liczby to 5-√-15 oraz 5+√-15. Sprawdzenie wyniku przeprowadził Cardano następująco:
"Nie zważając na tortury umysłu, jakie się z tym wiążą, pomnóżmy 5+√-15 przez 5-√-15. Otrzymujemy 25 - (-15), co jest 25 + 15. Zatem iloczyn jest równy 40.... To jest prawdziwie wyrafinowane."

No, to ile to jest: (1+√-1)(1-√-1)? Pomnóżmy. Pamiętajcie, że √-1×√-1=-1. Świetnie. A teraz trudniejsze zadanie: a+b√-1 przez a-b√-1 . Co wyszło? Na pewno tak: (a+b√-1) (a-b√-1)=a²+b²

Co w tym ciekawego? Na przykład to, że umiemy rozkładać na czynniki wyrażenia, których "przedtem" nie umieliśmy. Wzór skróconego mnożenia na a²-b² na pewno pamiętacie, a wzoru na a²+b² nie było, bo być nie mogło. W dziedzinie liczb rzeczywistych wielomian a²+b² jest nierozkładalny. Oznaczmy "nasz" pierwiastek z "minus jeden" literą i. A więc i²=-1. To jest pierwsza liczba "nierzeczywista". I właśnie ona opisuje nam obrót płaszczyzny o 90 stopni. Dlaczego? Przecież i²=-1, a złożenie jednego obrotu o 90 stopni i drugiego takiego samego obrotu daje obrót o 180 stopni. Jakim obrotem jest ten opisywany przez ? To jasne - obrotem o 45 stopni. A co opisuje liczba -i? To trochę trudniejsze:

(-i)² = -i×(-i) = + i² = -1

a więc -i opisuje też obrót o 90 stopni, tyle że w drugą stronę niż obrót wyznaczony przez i. Który z nich jest w lewo, a który w prawo? To się trzeba umówić. Przyjmujemy, że liczba i daje obrót w stronę, którą matematycy uważają za dodatnią: przeciwna do ruchu wskazówek zegara. Liczba -i opisuje obrót w stronę, w którą poruszają się wskazówki.

Czy jednak są takie liczby jak i oraz -i? Są! Właśnie powołaliśmy je do życia. Słucham? Że istnieją one tylko w naszej głowie? No tak, a czego oczekiwać? Wszystkie inne liczby też istnieją tylko w naszym umyśle. Musimy przetestować, czy nasze nowo narodzone liczby przeżyją. Mówiąc dokładniej, czy konstrukcja jest poprawna logicznie i czy one się do czegoś przydadzą. Proszę, uwierzcie mi na słowo, że wszystko jest w porządku i że te nowe liczby są naprawdę użyteczne. Liczby takie, jak 3+i , 5-7i , ogólniej: a+bi są nazywane liczbami zespolonymi. Pokazałem Wam, jak można je otrzymać za pomocą obrotów płaszczyzny. Można je wprowadzić inaczej: jako punkty płaszczyzny, jako pewne wielomiany, jako pewne tablice liczbowe... a za każdym razem chodzi o to samo: równanie x² + 1 = 0 nie ma pierwiastka... hokus-pokus i już ma!!!! Radujmy się i weselmy się!!!

Koniec wycieczki

Tu się kończy nasza pierwsza wycieczka po krainie liczb, które nie są rzeczywiste. Z innych nieziemskich liczb wspomnę jeszcze takie, które mają nieskończenie wiele cyfr z przodu, a nie z tyłu (nazywają się one 10-adyczne, ważniejsze dla nas są p-adyczne, gdzie p jest liczbą pierwszą), np.: X = .........96109004106619977392256259918212890625

Obliczmy sobie, proszę, X². Jak? A jakbyśmy obliczali kwadrat liczby, która ma nieskończoną liczbę cyfr z tyłu? No, to zróbmy podobnie. Przekonajmy się, że X² = X.

Znajdźmy inną taką liczbę z nieskończoną liczbą cyfr z przodu, która spełnia równanie. Wskazówka: kwadrat liczby, która kończy się na sześć, też kończy się na sześć. Kwadrat liczby, która kończy się na 76, też kończy się na 76. Kwadrat liczby, która kończy się na 376, też kończy się na 376. Kwadrat liczby, która kończy się na 9376, też kończy się na 9376. Kwadrat liczby, która kończy się na... Istnieją również liczby, które są tak małe, że choć dodatnie, pozostają mniejsze od każdej innej liczby dodatniej. Są one tak malutkie, że czasami już wystarczy je podnieść do kwadratu, żeby dostać zero. Istnieją liczby, które nie spełniają warunku a×b = b×a. Są i liczby nieskończone. Ile jest wszystkich liczb naturalnych? Nieskończenie wiele? No tak, ale ile? Jaką liczbą można to wyrazić? Odpowiedź: najmniejszą z liczb nieskończonych; oznacza ją się taką ładną literą: À i dopisuje wskaźnik zero À₀ , alef-zero.

Są też liczby, o których nie wiemy, czy istnieją... albo takie, w których istnienie można wierzyć, albo nie wierzyć, jak się tam komu podoba. A skoro o podobaniu się mowa: mam nadzieję, że wam wciąż podobają się Nierzeczywiste Liczby, Liczby z Gatunku Fantazy.