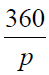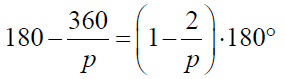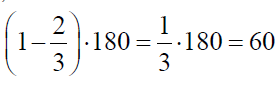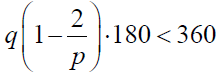Ścieżki i zarośla geometrii
Ja wracam do szkolnych lektur. Przeczytałem na nowo (nie po raz pierwszy na nowo) książkę Szczepana Jeleńskiego (1881-1949) „Lîlâvatî”. Niewielu Czytelnikom mówi coś samo to słowo. Jest to imię córki sławnego matematyka hinduskiego, znanego jako Bhâskara (1114- 1185), zwanego Acâria, czyli mędrzec, który swoją książkę o algebrze tym właśnie imieniem zatytułował. Później Lîlâvatî sama została znaną matematyczką i filozofką. Według innych źródeł to ona samodzielnie napisała tę książkę.
Tak samo nazwał swoją książkę o matematyce Szczepan Jeleński (pierwsze wydanie – 1926 r.). Może nawet trudno nazwać tę książkę dziełem matematycznym – był to raczej zestaw łamigłówek, ponadto w dużej części przepisanych ze źródeł francuskich (prawa autorskie w dzisiejszym sensie nie istniały). Tak czy owak, była to przez wiele lat jedyna polska książka popularna o matematyce – później doszła jeszcze druga książka Jeleńskiego, „Śladami Pitagorasa”. Młodzi ludzie interesujący się matematyką (a takim kiedyś byłem) mieli więc niewiele do wyboru…
za to „Lîlâvatî” wypadało znać niemal na pamięć…. Ech, to były czasy… Ich największą zaletą było to, że miałem wtedy… naście lat. Dzisiaj, z perspektywy porządnie wykształconego matematyka, zupełnie inaczej patrzę na „Lîlâvatî” – może tak, jak himalaista na zakosy ścieżki na Szpiglasową Przełęcz. Ani jedna, ani druga nie traci uroku… W charakterystycznym dla siebie stylu Szczepan Jeleński, wyznający w życiu prywatnym tzw. idee narodowe, pisze w przedmowie:
Liczba pod różnymi postaciami przeniknęła całe nasze życie współczesne, wdarła się w najwyższe nawet strefy zagadnień narodowych i międzynarodowych. Cóż więc praktycznie ważniejszym być może dla podniesienia sił narodu, jeśli nie wytworzenie w jego młodem pokoleniu, obok tężyzny fizycznej i moralnej, jak największej bystrości ku szybkiej a trafnej orientacji w nieustannej gmatwaninie interesów prywatnych i publicznych, która się wzmaga z dnia na dzień. A przy tym my, Polacy, sami niewielkie mając w tym kierunku skłonności, skazani jesteśmy na stałe współżycie z trzema narodami: żydowskim, niemieckim i czeskim, o szczególnych zdolnościach kombinacyjnych, wprost celującymi pod względem kalkulacji i rzutkości.
Jedną zaś z bardzo skutecznych pomocy do zdobycia tego rodzaju giętkości umysłu są właśnie rozrywki matematyczne. Należy więc pragnąć, ażeby Polacy potrafili dostrzec w nich owe wielkie wartości gimnastyki umysłowej, która każdemu, dosłownie każdemu w życiu się współczesnem przydać może. Doskonalenie swych ośrodków w kierunku większej spostrzegawczości praktycznej, przydatne jest bardzo nietylko kupcowi lub przemysłowcowi, potrzebne jest ono dziś również rolnikowi, urzędnikowi, rękodzielnikowi, nawet robotnikowi, jak to wykazuje dążenie do osiągnięcia maximum wyników pracy przy minimum wysiłku fizycznego, zwane systemem Taylora.
Nie odnosząc się do opisu cech narodowych, powiem, że po dziewięćdziesięciu latach słowa Jeleńskiego o matematyce nie straciły aktualności. Matematyka uczy myślenia. To fakt. Czy moglibyśmy uczyć myślenia inaczej, prościej i przyjemniej? Być może. Tylko… wciąż nie potrafimy. Tłumaczę swoim niechętnym do matematyki studentom, że jest to również test na ich zdolności umysłowe. Jeżeli nie potrafisz nauczyć się naprawdę prostej teorii matematycznej, to… może z twoimi zdolnościami umysłowymi jest gorzej, niż byśmy obaj (oboje) chcieli...?
Znaki na piasku
I oto pierwszą opowieścią w „Lîlâvatî” jest historia opisana przez filozofa francuskiego Josepha de Maistre (1753-1821).
Pewien marynarz z rozbitego okrętu został wyrzucony przez fale na pusty brzeg wyspy – jak sądził, bezludnej. Nagle ujrzał na piasku nadbrzeżnym ślad nakreślonej przed kogoś figury geometrycznej. Wtedy zrozumiał, że wyspa nie jest bezludna!
Cytując de Maistrego, pisze Jeleński: „Gdyby ten znikomy zarys na lotnym piasku nie był figurą geometryczną, byłby dla nieszczęsnego rozbitka wyrazem niemym, dziełem przypadku, ale on mu wykazał od pierwszego wejrzenia proporcję i liczbę, a to zwiastowało człowieka oświeconego”. Tyle historia.
Zauważmy, że taką samą reakcję wywołałoby u marynarza np. narysowanie litery K, … a także dowolne inne ślady obecności ludzkiej. Geometria jest tu wyidealizowana.
Tym niemniej astronom Camille Flammarion (1847-1925) proponował, by geometrią pozdrawiały się na odległość cywilizacje. Dostrzegał to jako jedynie słuszne i możliwe próby porozumienia się. Wyświetlimy takim Marsjanom trójkąty pitagorejskie… oni nam odpowiedzą Talesem, my im wzory Viete’a, oni okrąg wpisany w trójkąt i oto przyjaźń nawiązana…
Do pomysłu tego wracali tacy pisarze, jak Jules Verne i Stanisław Lem. A w 1972 r. płytki z rysunkami geometrycznymi (i nie tylko) umieszczono na pokładzie sondy Pionier, która wciąż przemierza bezkres Kosmosu, oddalona teraz od nas już o prawie 140 jednostek astronomicznych (1 j.a. to średnia odległość Ziemi od Słońca, czyli ok. 149 milionów km). Płytki zaprojektował m.in. astronom Frank Drake, twórca kontrowersyjnej reguły, mówiącej o liczbie cywilizacji pozaziemskich.
Z geometrią to w ogóle jest niesamowicie. Wszyscy znamy powszechny pogląd na pochodzenie tej nauki. Po prostu zaczęliśmy (my, ludzie) mierzyć ziemię (a potem i Ziemię) w celach jak najbardziej użytkowych. Określanie odległości, prowadzenie linii prostych, wytyczanie kątów prostych, obliczanie objętości stawało się powoli koniecznością. I stąd cała geometria („mierzenie ziemi”), stąd cała matematyka…
Od pewnego czasu jednak ten jasny obraz historii nauki zaciera nam się. Gdyby bowiem matematyka potrzebna była wyłącznie w celach użytkowych, nie troszczylibyśmy się o dowodzenie prostych twierdzeń. „Przecież widać, że to musi być ogólnie prawdą”, powie każdy po sprawdzeniu, że w kilku trójkątach prostokątnych suma kwadratów przyprostokątnych jest równa kwadratowi przeciwprostokątnej. Po co aż taki formalizm?
Placek ze śliwkami ma być smaczny, program komputerowy ma działać, samochód musi jeździć. Jeżeli trzydzieści razy obliczyłem pojemność jakiejś beczki i było dobrze, to po co jeszcze uzasadnienie?
Tymczasem starożytnym Grekom przyszło do głowy, że trzeba wykoncypować jakiś formalny dowód.
Matematyka zaczyna się więc od Talesa (625- 547 p.n.e.). Przyjmuje się, że to w Milecie zaczęto się zastanawiać, dlaczego. Inteligentnym ludziom nie wystarczyło, że coś widzą, że o czymś są przekonani. Dostrzegli potrzebę dowodu, logicznego ciągu argumentów od założenia do tezy.
Chcieli też czegoś więcej. Prawdopodobnie to Tales pierwszy próbował wyjaśnić zjawiska fizyczne w naturalistyczny sposób, bez boskiej interwencji. Filozofia europejska zaczęła się od filozofii przyrody – od tego, co jest już za fizyką (stąd nazwa: metafizyka). Ale fundament europejskiej ontologii i filozofii przyrody położyli pitagorejczycy (Pitagoras, ok. 580- ok. 500 p.n.e.).
Założył on w Krotonie na południu Półwyspu Apenińskiego własną szkołę – dziś nazwalibyśmy ją może sektą. Nauka (w dzisiejszym sensie tego słowa), mistyka, religia i fantazjowanie mieszały się tam dość dokładnie. Bardzo ładnie przedstawił lekcje matematyki w niemieckim gimnazjum Thomas Mann w powieści „Doktor Faustus”. W przekładzie Marii Kureckiej i Witolda Wirpszy fragment ten brzmi:
Notując i wznosząc niekiedy oczy ku łagodnie uśmiechniętej twarzy profesora o białej grzywie, chłonęliśmy ową wczesną koncepcję kosmologiczną, wytwór surowego a nabożnego umysłu, który główną swoją namiętność, matematykę, abstrakcyjne proporcje, liczbę, podniósł do rangi głównej zasady powstania i istnienia świata i stając jako wtajemniczony mędrzec wobec całokształtu zjawisk pierwszy, z wielkim gestem, nazwał je był „Kosmosem” jako ład i harmonię, ponadzmysłowy system dźwięcznych interwałów sferycznych.
Liczba i stosunki liczb jako pojęcie leżące u podstaw bytu i moralnej godności – ogromne sprawiało wrażenie, jak wszystko, co piękne, ścisłe, etyczne, zespalało się tu uroczyście w ideę autorytetu, ożywiającą cały związek pitagorejczyków, ezoteryczną szkołę religijnej odnowy życia, milczącego posłuszeństwa i ścisłego podporządkowania się zasadzie „autós épha”.
W interesującej książce „Historia wiedzy od zarania dziejów do dziś” Charlesa van Dorena znalazłem bardzo ciekawy punkt widzenia. W jednym z rozdziałów autor opisuje znaczenie szkoły pitagorejskiej. Zdumiał mnie sam tytuł rozdziału. Brzmi on: „Wynalezienie matematyki: pitagorejczycy”.
Często dyskutujemy, czy teorie matematyczne się odkrywa (tak jak nieznane lądy), czy wynajduje (tak, jak nieistniejące przedtem maszyny). Część twórczych matematyków widzi siebie jako odkrywców, inni postrzegają siebie jako wynalazców albo konstruktorów, rzadziej rachmistrzów.
Ale autor wspomnianej książki pisze o wynalezieniu samej matematyki, jako całości.
Od przesady do manowców
Po tej przydługiej części wstępnej przejdę do samej geometrii, do opisania, jak przesadna wiara w geometrię może poprowadzić uczonego na manowce. Johannes Kepler znany jest w fizyce i astronomii jako odkrywca trzech praw ruchu ciał niebieskich. Po pierwsze, każda planeta Układu Słonecznego porusza się wokół Słońca po orbicie w kształcie elipsy, w której w jednym z ognisk jest Słońce. Po drugie, w równych odstępach czasu promień wodzący planety, poprowadzony od Słońca, zakreśla równe pola. Po trzecie, stosunek kwadratu okresu obiegu planety wokół Słońca do sześcianu wielkiej półosi jej orbity (czyli średniej odległości od Słońca) jest stały dla wszystkich planet w Układzie Słonecznym.
Być może to trzecie prawo – do ustalenia którego potrzeba było wielu danych i wielu obliczeń, skłoniło Keplera do dalszych poszukiwań regularności w ruchu i położeniu planet. Historia jego nowego „odkrycia” jest wielce pouczająca. Od starożytności zachwycamy się nie tylko wielościanami foremnymi, ale i rozumowaniem, które pokazuje, że w przestrzeni jest ich tylko pięć. Wielościan trójwymiarowy nazywamy foremnym, jeśli jego ściany są takimi samymi wielokątami foremnymi i w każdym wierzchołku schodzi się tyle samo krawędzi. Poglądowo: każde naroże wielościanu foremnego musi „wyglądać tak samo”. Najbardziej znanym wielościanem jest sześcian. Regularną kostkę każdy widział.
Mniej znany jest czworościan foremny, a w szkole występuje pod nazwą ostrosłupa prawidłowego trójkątnego. Wygląda jak piramida. Pozostałe trzy wielościany foremne są mniej znane. Ośmiościan powstaje, gdy połączymy środki krawędzi sześcianu. Dwunastościan i dwudziestościan wyglądają już jak piłki. Uszyte z miękkiej skóry, nadawałyby się do kopania . Rozumowanie, że nie ma innych wielościanów foremnych niż pięć brył platońskich, jest bardzo ładne. Najpierw zdajmy sobie sprawę, że jeżeli bryła jest foremna, to w każdym wierzchołku musi się schodzić tyle samo (niech to będzie q) takich samych wielokątów foremnych, niech to będą p-kąty. Musimy sobie teraz przypomnieć, jaki jest kąt w wielokącie foremnym. Jeśli ktoś nie pamięta ze szkoły, to przypominamy, jak się znajduje odpowiedni wzór. Wyruszamy w podróż dookoła po p-kącie. W każdym wierzchołku skręcamy o ten sam kąt a. Gdy objedziemy wielokąt i wrócimy do punktu wyjścia, wykonaliśmy p takich skrętów, no a łącznie obróciliśmy się o 360 stopni.
Czyli α to 
stopni.
Ale α jest przecież dopełnieniem do 180 stopni kąta, który chcemy obliczyć, a który jest wobec tego równy
Znaleźliśmy wzór na kąt (matematyk powiedziałby: miarę kąta) wielokąta foremnego. Sprawdźmy: trójkąt ma p = 3, no a
Zgadza się. Gdy p = 4 (kwadrat), to
stopni i też jest dobrze.
Co otrzymamy dla pięciokąta? Co się więc dzieje, gdy q wielokątów, z których każdy ma p takich samych kątów
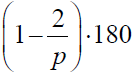stopni, schodzi się w jednym wierzchołku? Gdyby to było na płaszczyźnie, to utworzyłby się kąt
stopni i nie mógłby być większy niż 360 stopni – bo wtedy wielokąty by na siebie zachodziły.
Ponieważ jednak wielokąty te schodzą się w przestrzeni, kąt musi być mniejszy niż cały kąt pełny.
I oto nierówność, z której wszystko wynika:
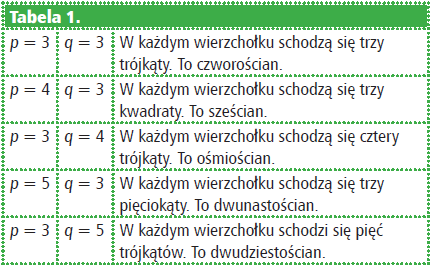
Podzielmy ją przez 180, pomnóżmy obie strony przez p, uporządkujmy (p–2)(q–2) < 4. Co z niej wynika? Zdajmy sobie sprawę z tego, że p oraz q mają być liczbami naturalnymi i że p > 2 (dlaczego? a co to jest p?) i podobnie q > 2. Nie ma wiele możliwości stworzenia iloczynu mniejszego niż 4 z dwóch liczb naturalnych. Zestawimy je wszystkie w tabeli 1.
Nie zamieszczam rysunków, każdy może sobie obejrzeć te bryły w Internecie… W Internecie… Nie odmówię sobie dygresji – może interesującej dla młodych Czytelników. W 1970 r. miałem referat na seminarium. Temat był trudny. Miałem mało czasu na przygotowanie, siedziałem wieczorami. Podstawowy artykuł był dostępny tylko do czytania na miejscu. Miejsce było przytulne, tchnące atmosferą pracy, Cóż, o siódmej zamykano. Wtedy narzeczona (obecnie żona) sama zaproponowała, że przepisze mi cały artykuł: kilkanaście stron druku. Przepisała (nie,nie gęsim piórem, mieliśmy już nawet długopisy), referat się udał. Dziś próbowałem znaleźć tę publikację, starą już przecież. Pamiętałem tylko nazwisko autora… Poszukiwania w Internecie trwały bardzo długo… całe piętnaście minut. Myślę o tym z uśmieszkiem i lekkim, nieuzasadnionym żalem.
Wracamy do Keplera i geometrii. Podobno Platon przewidział istnienie piątej bryły foremnej, bo brakowało mu właśnie czegoś unifikującego, obejmującego cały świat. Być może nawet dlatego polecił uczniowi (Teajtet) jej szukać. Jak było, tak było, grunt, że dwunastościan został odkryty. Tę postawę Platona nazywamy panteizmem. Ulegali jej w mniejszym czy większym stopniu wszyscy uczeni, aż do Newtona włącznie. Od bardzo racjonalnego XVIII wieku jej wpływ radykalnie się zmniejszył, choć nie należy się wstydzić, że do pewnego stopnia ulegamy jej wszyscy.
W keplerowskiej koncepcji budowy Układu Słonecznego wszystko się zgadzało, dane doświadczalne pasowały do teorii, teoria była logicznie uzasadniona, bardzo piękna... tyle, że kompletnie fałszywa. W jego czasach znano tylko sześć planet: Merkury, Wenus, Ziemia, Mars, Jowisz i Saturn. Dlaczego planet jest akurat sześć? zapytał Kepler. I jaka prawidłowość rządzi ich odległością od Słońca? Założył on, że wszystko się ze sobą łączy, że geometria i kosmogonia są ściśle ze sobą związane. Z dzieł starożytnych Greków wiedział, że jest tylko pięć wielościanów foremnych. Spostrzegł, że między sześcioma orbitami jest pięć wolnych przestrzeni. Może zatem każda z tych wolnych przestrzeni odpowiada jakiemuś wielościanowi foremnemu?
Po kilku latach obserwacji i pracy teoretycznej stworzył następującą teorię, za pomocą której wyliczył całkiem dokładnie rozmiary orbit, a którą przedstawił w opublikowanej w 1596 r. książce „Mysterium Cosmographicum”: Wyobraźmy sobie olbrzymią kulę, której średnicą jest średnica orbity Merkurego w jego rocznym ruchu dokoła Słońca. Wyobraźmy sobie następnie, że na tej kuli jest opisany ośmiościan foremny, na nim kula, na niej dwudziestościan, na nim znowu kula, na niej dwunastościan, na nim kolejna kula, na niej czworościan, potem znowu kula, sześcian i w końcu na tym sześcianie jest opisana kula.
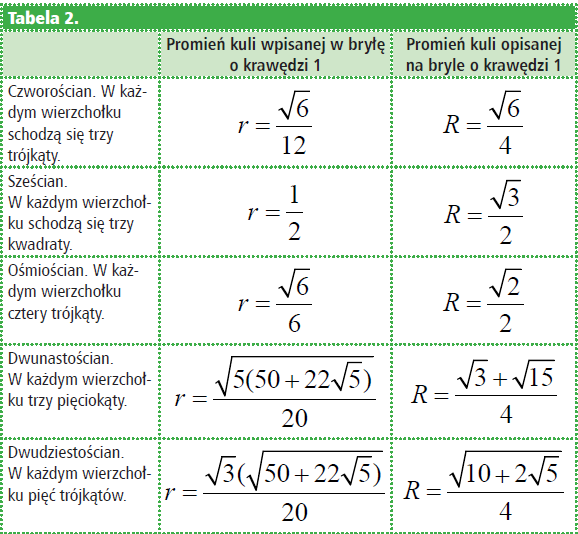
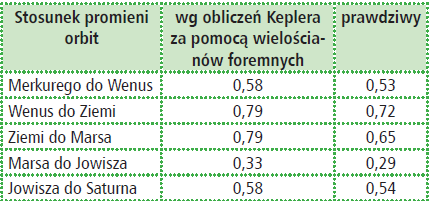
Kepler doszedł do wniosku, że średnice tych kolejnych kul są średnicami orbit kolejnych planet: Merkurego, Wenus, Ziemi, Marsa, Jowisza i Saturna. Wydawało się, że teoria jest bardzo trafna. Niestety – zgadzała się bowiem z danymi eksperymentalnymi. A cóż może lepiej świadczyć o słuszności teorii matematycznej niż jej zgodność z danymi eksperymentalnymi lub danymi obserwacyjnymi, szczególnie tymi „wziętymi z nieba”. Zbiorę te obliczenia w tabeli 2. Co więc zrobił Kepler? Próbował, próbował, aż wyszło, to znaczy, gdy konfiguracja (kolejność sfer) i wynikające z niej obliczenia zgadzały się z danymi obserwacyjnymi. Oto współczesne dane i rachunki Keplera:
Można było ulec urokowi teorii i wierzyć, że to pomiary na niebie są niedokładne, a nie rachunki wykonane w zaciszu pracowni. Niestety, dzisiaj wiemy, że jest co najmniej dziewięć planet, a cała zbieżność rezultatów stanowi jedynie dzieło przypadku. Szkoda. Takie to było ładne...
