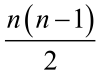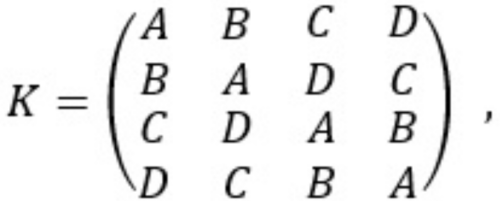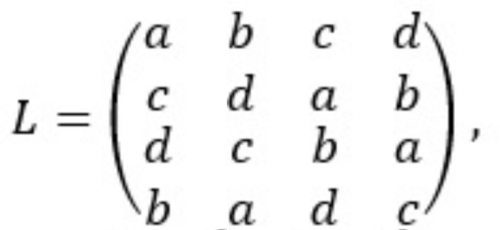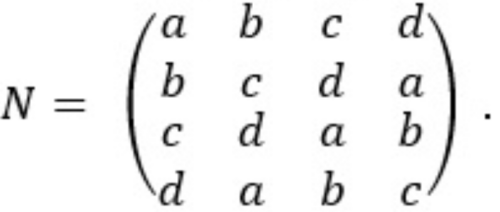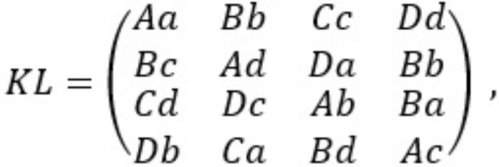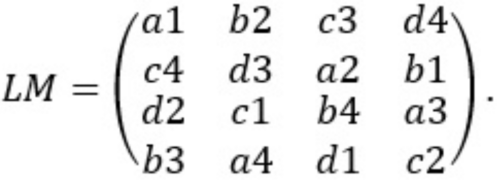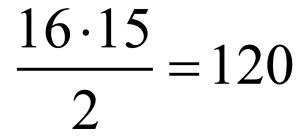Znowu o pandemii i matematyce

Ale przecież mam pisać o matematyce. Nie ja jeden doszedłem do wniosku, że musimy uczyć naszych uczniów i studentów zupełnie, ale to zupełnie inaczej niż, powiedzmy, 10 lat temu. Zmiany zostały wymuszone nie tylko przez pandemię, ale i przez zwariowane przyspieszenie, jakim podlega nasz współczesny świat. Trzydzieści lat temu na moim osiedlu (kilka tysięcy mieszkańców) było pięć automatów telefonicznych. Obecnie w moim mieszkaniu jest pięć telefonów i pięć komputerów. No cóż, wciąż wydaje mi się to dziwne.
Bardzo często kupujemy coś przez Internet, towary sprawnie są dostarczane do domu albo do niedalekiego paczkomatu. Zaprojektowanie trasy kuriera, który ma doręczyć kilkadziesiąt przesyłek, wiąże się z matematyką z naprawdę najwyższej półki. Nie znam się dobrze na algorytmach problemu komiwojażera, bo tak się nazywa zagadnienie ekonomicznego dotarcia do wielu punktów, rozrzuconych po okolicy.
Staram się oglądać w telewizji tylko programy sportowe. Od dawna interesowałem się "matematyką sportu". Dzisiaj zatem dwa zagadnienia o planowaniu rozgrywek. Pokazują one, że Królowa Nauk ma zastosowania nie tylko w inżynierii budowlanej.
Sprint narciarski
W zawodach sprintu narciarskiego startuje na ogół 30 zawodników. Rozgrywane są od razu ćwierćfinały: pięć biegów po sześciu zawodników lub zawodniczek. Do półfinału wchodzą zdobywcy pierwszych i drugich miejsc i dodatkowo tzw. lucky losers, szczęśliwi przegrani - dwóch (dwie) z najlepszymi czasami z pozostałych. Ale ciekawa - i wcale nieelementarna - matematyka wchodzi na samym starcie.
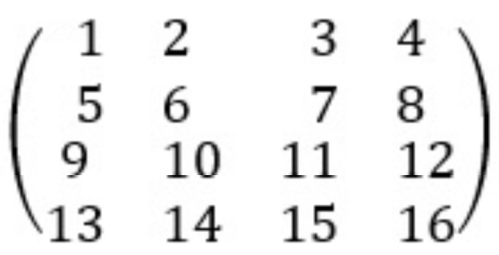
Według regulacji międzynarodowej federacji narciarskiej zawodników o kolejnych numerach rankingowych rozstawia się w eliminacjach (które są de facto ćwierćfinałami) w następujący sposób. Od razu napiszę prostokątną tablicę. Sądzę, że większość Czytelników wie, że matematycy nazywają taką tablicę macierzą. To po prostu przekład słowa "matryca". Będziemy ją nazywać macierzą rozstawienia.
Poziome rzędy takiej tablicy nazywają się jej wierszami, pionowe - kolumnami. W pięciu kolejnych biegach startują zawodnicy o numerach z poszczególnych wierszy: w pierwszym biegu 1, 10, 11, 20, 21, 30 itd.
Spójrzmy, jak misterny matematycznie jest to układ - jak subtelnie łączy porządek z przypadkowością. W każdym wierszu i w każdej kolumnie po każdej liczbie parzystej następuje nieparzysta i na odwrót. Możemy to wyrazić, przyporządkowując każdej liczbie parzystej zero, a nieparzystej 1. Wtedy tablica wygląda tak
a jeżeli zamiast zera i jedynek postawimy pola białe i czarne, to zobaczymy kawałek zwykłej szachownicy. Na niej pola białe i czarne są, że tak określę, przemieszane w pewnym porządku.
Zobaczmy, jak wygląda tablica w świetle "modulo 3" - to znaczy, że różnym kolorom odpowiadają reszty z dzielenia liczb tablicy przez 3.
A oto nasza tablica biegów narciarskich, rozpatrywana modulo 5. W ostatnim pasku wszystkie pola są tego samego koloru, bo wszystkie liczby są podzielne przez 5. Pozostałe pola tego samego koloru są połączone ruchem konika szachowego.
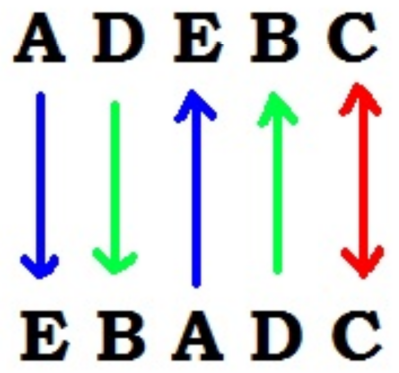
Spójrzmy teraz na kolumny naszej macierzy rozstawienia. W pierwszej z nich są liczby z pierwszej piątki, ustawione w kolejności 1, 4, 5, 2, 3. Zastępując liczby kolejnymi literami, możemy określić to jako porządek ADEBC. Liczby drugiej kolumny są ustawione w kolejności 10, 7, 6, 9, 8, co daje EBADC. Porządki te związane są następująco:
Jeśli pamiętasz, Czytelniku, co to są permutacje, to masz to właśnie. Widzimy permutacje wzajemnie odwrotne do siebie. To jest kolejny przykład subtelnego połączenia dobrego przemieszania z pewną regularnością.
Wobec tego krótki kurs teorii permutacji. Pamiętamy pewnie, co to jest permutacja: to ustawienie liczb, liter, przedmiotów, w pewnym porządku, w pewnej kolejności. Permutacja 1, 2, 3, 4, 5 (na literach ABCDE) nazywana jest tożsamościową.
Jeżeli w permutacji większa liczba stoi przed mniejszą (późniejsza litera alfabetu przed wcześniejszą), to mówimy, że para ta tworzy inwersję. Na przykład w permutacji 1, 2, 3, 5, 4 jest jedna inwersja, w permutacji 2, 3, 4, 5, 1 są cztery, a w permutacji 5, 4, 3, 2, 1 najwięcej, ile może być dla pięciu elementów: 10.
Obliczmy ogólnie, ile inwersji ma permutacja, która ustawia elementy w porządku odwrotnym do naturalnego: 5, 4, 3, 2, 1, albo e, d, c, b, a. Jeżeli liczb jest n, to w takiej permutacji każda liczba tworzy inwersję z każdą inną. Wynika stąd, że mamy tu
inwersji. Iloczyn n(n-1) trzeba było podzielić przez 2, bo inaczej każdą inwersję liczylibyśmy dwa razy.
Do każdej permutacji istnieje do niej odwrotna. Mówiąc obrazowo, jeżeli permutację traktujemy jako pomieszanie czegoś, to permutacja odwrotna przywraca naturalny porządek. Na przykład permutacją odwrotną do 3, 4, 1, 5, 2 jest 3, 5, 1, 2, 4. Można to łatwo zrozumieć w ten sposób. Jeżeli mamy ustawienie 3, 4, 1, 5, 2, to naturalny porządek przywrócimy, ustawiając te liczby w porządku: trzecia (jest nią 1), piąta (to jest 2), pierwsza (=3), druga (=4), czwarta (=5). Bywa, że permutacja jest sama do siebie odwrotna, na przykład 2, 1, 3, 5, 4. Tę własność ma i permutacja 5, 4, 3, 2, 1.
Zróbmy kolejną obserwację dotyczącą rozstawienia zawodników. Rozpatrzymy permutacje wyznaczone przez kolumny macierzy rozproszenia, to jest 1, 4, 5, 2, 3, potem 10, 7, 6, 9, 8 i dalej. Po zamianie liczb na litery będą to permutacje ADEBC, EBADC, potem znów ADEBC, EBADC i jeszcze raz to samo: ADEBC, EBADC. Permutacje ADEBC i EBADC są zaś do siebie wzajemnie odwrotne.
Poszczególne biegi powinny być wyrównane; zatem najlepiej będzie, gdy we wszystkich średnia rankingów będzie taka sama. Ale powinny być też zbliżone pod względem rozproszenia. Nie byłoby dobrze, gdyby w jednym biegu startowały numery 1, 2, 3, 18, 19, 20, a w drugim 8, 9, 10, 11, 12, 13.
Miarą rozproszenia w statystyce jest odchylenie standardowe. Określamy je jako pierwiastek sumy kwadratów odchyleń od średniej, ale to byłaby za męcząca wycieczka w wyższą matematykę.
Przyjrzyjmy się innym, subtelnym zależnościom, rządzącym ustawieniem zawodników. Kilka następnych zdań będzie zrozumiałych dla Czytelników znających algebrę liniową. Otóż rząd macierzy rozstawienia wynosi 2, a więc najmniej, jak może być dla liczb od 1 do 30. To dodatkowy argument, że wymyślone przez federację rozstawienie łączy regularność z przypadkowością. Zauważmy jeszcze, że system zapewnia, że dwaj najwyżej klasyfikowani zawodnicy spotkają się dopiero w finale. Jest zupełnie zrozumiałe, że tak powinno być. Biorąc to wszystko pod uwagę, widzimy, że federacja narciarska zatrudniła dobrego matematyka do układania schematu biegów sprinterskich.
Wróćmy do ciekawej i niełatwej, ale elementarnej matematyki.
Wyścigi na żużlu
Przyznam się, że nie rozumiem popularności tego sportu, ale nie o to idzie. Tu problem rozstawiania naprawdę dotyka poważnej matematyki. Najpierw wobec tego "wstęp teoretyczny".
Leonard Euler (1707-1783, szwajcarski matematyk i fizyk, który wiele lat spędził w Petersburgu) rozważał problem, który wydaje się czystą łamigłówką, bez praktycznych zastosowań. Sześć pułków wysyła na defiladę po sześciu oficerów różnych rang. Czy można ich ustawić w kwadrat 6 na 6 tak, by w żadnym rzędzie ani w żadnej kolumnie nie powtarzały się pułki ani stopnie?
Rozważmy ogólniejsze zagadnienie. Niech n2 oficerów przybywa z n różnych pułków. Łatwo zestawić szyk tak, by w każdym rzędzie i w każdej kolumnie każdy pułk miał swojego reprezentanta. Oto jedno z możliwych ustawień. Ponumerujmy pułki od 0 do n-1. Na miejscu (i, j) kwadratu do defilady postawmy oficera z pułku o numerze i+j mod n. Symbol mod n oznacza, że daną liczbę dzielimy przez n i bierzemy resztę z tego dzielenia. Gdy n=6, mamy
Kwadrat zawierający n2 liczb od 1 do n tak, żeby ani w rzędach poziomych, ani w pionowych kolumnach nie powtarzały się te same liczby, nazywamy kwadratem łacińskim. Nazwa pochodzi z dawnych przyzwyczajeń używania tu liter alfabetu łacińskiego, a nie liczb.
Ten sam kwadrat możemy otrzymać w inny sposób, też algebraiczny. Zamiast dodawania, rozpatrujmy mnożenie modulo 7. To tak, jakby mnożyć dni tygodnia: 3 razy czwartek to odstęp 12 dni, czyli od poniedziałku do następnego piątku: 3·4=12≡5 mod 7 itd. Ułóżmy tabelkę mnożenia liczb modulo 7:
Czy widać, że jest to "taka sama" tabelka, jak poprzednia. Należy trochę zmienić porządek. Liczby 1, 2, 3, 4, 5, 6 ustawiamy w porządku 1, 3, 2, 6, 4, 5 i przenumerowujemy na 0, 1, 2, 3, 4, 5.
Kwadrat, który ułożyliśmy, jest zupełny - każda liczba sąsiaduje z każdą, zarówno w rzędzie, jak i w kolumnie. Na defiladzie będzie taki generał, który będzie szedł koło porucznika, a jakiś kapitan koło admirała. Gdyby serię znaczków pocztowych wydać w arkusiku ułożonym w kwadrat łaciński zupełny, filateliści mieliby gratkę: dałoby się zbierać znaczki parami, każdy koło każdego. Wszystkie kwadraty łacińskie, ułożone według reguły mnożenia modulo pewna liczba pierwsza p, są zupełne.
W terminologii, wyjaśnionej w następnym akapicie, taki kwadrat jest ortogonalny do swojej transpozycji.
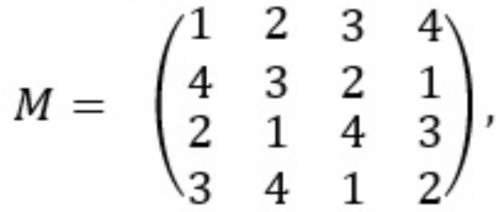
Matematyka robi się, jak widać, coraz trudniejsza. Powróćmy do wyjściowego zadania o defilowaniu. Do jego rozwiązania potrzebne są kwadraty ortogonalne. Popatrzmy na pierwsze trzy z czterech kwadratów:
Nałóżmy pierwszy z nich na drugi, potem pierwszy na trzeci i wreszcie drugi na trzeci. Otrzymamy kolejno
W każdym z nich symbole poszczególnych typów mieszają się w najlepszy możliwy sposób: każdy z każdym, przy czym ani w wierszach, ani w kolumnach nie ma powtórzeń. Jeśli tak jest, to kwadraty K i L (a także kwadraty K, M oraz L, M) nazywamy ortogonalnymi. Kwadraty KL, KM i LM nazywamy już grecko-łacińskimi; pochodzi to stąd, że Euler oznaczał elementy tych kwadratów literami łacińskimi i greckimi.
Zadanie (dla moich studentów wyższej szkoły informatycznej było całkiem trudne). Wykaż, że dla kwadratu N nie istnieje ortogonalny.
I tu dochodzimy do wyścigów motocyklowych. W zawodach bierze udział 16 zawodników. W każdym biegu startuje czterech. Należy zaplanować biegi tak, żeby każdy spotkał się z każdym jeden raz. Ile biegów jest potrzebnych? Jak je rozplanować?
Każdy zawodnik startuje w pięciu biegach i ma za każdym razem trzech innych konkurentów, a więc spotyka się z każdym z pozostałych. Gdyby jeździli po dwóch, potrzeba by było
biegów. Ponieważ startują po czterech, wystarczy sześć razy mniej. Oto jak. Przypominamy sobie ortogonalne kwadraty łacińskie. Spójrzmy na kwadraty KL, KM i LM. Pierwszych osiem biegów puszczamy według rzędów poziomych i pionowych tabeli:
Wiersze: (1-2-3-4) (5-6-7-8) (9-10-11-12) (13-14-15-16)
Kolumny: (1-5 -9-13) (2 -6-10-14) (3-7-11-15) (4-8-12-16)
Następnie patrzymy na pozycje litery A w pierwszym kwadracie. Są to kolejno pozycje 1, 6, 11, 12. Ci zawodnicy startują w biegu dziewiątym. W dziesiątym rozważamy miejsca litery B w pierwszym kwadracie, potem C, D i przechodzimy do następnego kwadratu (litery a, b, c, d) i trzeciego (liczby 1, 2, 3, 4). Otrzymujemy taką kolejność biegów 9-20:
A: (1-6-11-12) B: ( 2-5-12-15) C: (3-8-9-14) D: (4-7-10-16)
a: (1-14-7-12) b: (2-8-11-13) c: (3-5-10-16) d: (4-6-9-15)
1: (1-8-10-15) 2: (2-7-9-16) 3: (3-6-12-13) 4: (4-5-11-14)
Zdziwiliby się mistrzowie ryczących silników, gdyby wiedzieli, że ocierają się o teorię ortogonalnych kwadratów łacińskich. Chociaż może by się wcale nie zdziwili, bo nic by to im nie powiedziało. Ale nie każdy musi umieć wszystko. Ja nie mam prawa jazdy na motocykl.
Dochodzimy jednak do matematyki z wysokiej półki. Już Leonard Euler podejrzewał, że nie da się ułożyć kwadratu grecko-łacińskiego z sześciu rzędów i sześciu kolumn. W 1782 roku sformułował ogólniejszą hipotezę, że nie da się ułożyć takiego kwadratu z żadnej liczby postaci n=4k+2. W 1959 roku Bose, Shrikhande i Parker wykazali fałszywość tej hipotezy Eulera dla n>6, to znaczy ułożyli kwadraty dowolnego rzędu n=4k+2, dla n>6. Kwadratu grecko-łacińskiego rzędu 6 do tej pory nie ma.
Może nie ma, bo nie może być, a może nikt nie wpadł na stosowny pomysł.
Michał Szurek