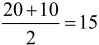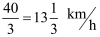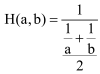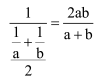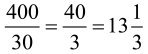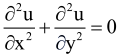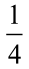Matematyka i rower

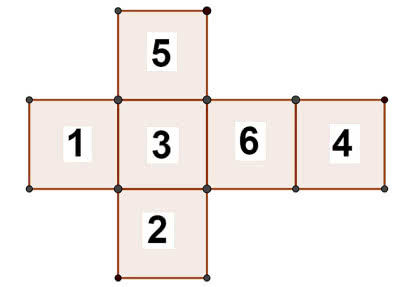
Na kostce do gry liczby rozmieszczone są tak, by suma na przeciwległych ściankach była zawsze równa 7. Dodajmy: 1+2+3+4+5+6=21. Takie liczby (będące sumami kolejnych liczb naturalnych) nazywamy trójkątnymi, a więc 21 jest liczbą trójkątną (1).
Po inne szczegóły odsyłam do poprzednich numerów, a jeszcze tylko trzy ciekawostki sportowe, dotyczące liczby 21. W siatkówce plażowej set polega na zdobyciu 21 punktów, a koszykówce 3×3 zdobycie 21 punktów przez jedną z drużyn oznacza koniec meczu przed czasem. W Tour de France jest zwykle 21 etapów.
No, właśnie - rower jest wdzięcznym gadżetem w szkolnych zadaniach matematycznych. Zacznę od zadania, sprawiającego kłopoty uczniom i studentom, nawet studentom informatyki, z którymi od lat mam do czynienia. Nieco złośliwie powiem, że nie było studenta… no, pewnego wydziału na UW, który by w pełni zrozumiał rozwiązanie. "Jak mogę pamiętać coś z matematyki, kiedy maturę zdawałem półtora roku temu?"
Zadanie 1. Wybrałem się na dwugodzinną okrężną przejażdżkę rowerową. Przez pierwszą godzinę pedałowałem dzielnie z prędkością 20 km/h, ale drugą wlokłem się tylko z prędkością 10 km/h. Cóż, jestem starszym panem. Jaka była moja średnia na całej trasie?
Odpowiedź wydaje się - i jest - bardzo prosta. Średnia to średnia. Dodajemy i dzielimy przez 2;.
Piętnaście kilometrów na godzinę.
Następnego dnia wybrałem się na przejażdżkę po tym samym lesie, ale z wybranym punktem docelowym. Chciałem dojechać do pewnej znanej mi ładnej polany. Było do niej 20 kilometrów. Jak poprzednio, w tamtą stronę udało mi się utrzymać prędkość 20 km/h, ale zmęczyłem się tak, że w drodze powrotnej moja średnia spadła do 10 km/h. Jaka była moja prędkość na całej trasie?
Jak to jaka? - dziwili się zawsze (!) uczniowie i studenci. Przecież to to samo. Pół drogi z taką prędkością, pół z taką. Średnia to średnia. Dodajemy i dzielimy przez dwa, bo przecież "połowy" są równe. Piętnaście!
Hm. Spójrzmy. Moja wycieczka drugiego dnia trwała trzy godziny (godzinę w jedną i dwie z powrotem). Przejechałem 40 kilometrów. To znaczy, że średnia prędkość wyniosła
, a nie piętnaście. No jasne: przecież wolniejsza jazda trwała dłużej, więc musiała mieć większy wpływ na średnią.
Matematycznie ujmuje się to tak: w tej sytuacji średnia prędkość nie jest średnią arytmetyczną, tylko harmoniczną prędkości składowych. Średnia harmoniczna jest to odwrotność średniej arytmetycznej odwrotności. Zapiszmy to wzorem:
Wygląda to mało zachęcająco, ale ułamki piętrowe nie są przecież tak straszne. Mamy
Zgadza się: gdy a=20, b=10, otrzymujemy
A oto zadanie 2, w gruncie rzeczy też rowerowe.
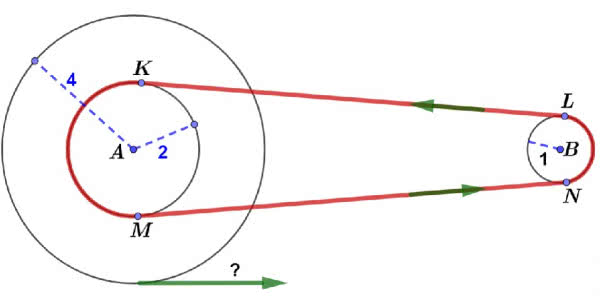
Koło zębate B o promieniu 1 cm połączone jest z przerzutką o środku w A. Jeżeli koło B obraca się z prędkością b obrotów na sekundę, to z jaką prędkością w cm/s porusza się punkt na obwodzie większego koła o promieniu 4? (2).
Rozwiązania nie podam, jest proste. Natomiast pozornie równie łatwe zadanie wyznaczenia długości czerwonej linii (a więc łańcucha rowerowego) wykracza już poza wiedzę szkolną. Jeszcze bardziej skomplikowana matematyka jest potrzebna przy projektowaniu kół zębatych. Jak je zaprojektować, by jak najlepiej przenosiły ruch z jednego koła na drugie?
Wróćmy do łatwiejszych zadań. Ale nie będzie sztampowo.
Zadanie 3. Na etapie Tour de Pologne samotny kolarz zyskał przewagę 5 minut nad peletonem. Osłabł jednak i może jechać tylko z prędkością 35 km/h. Peleton jedzie 45 na godzinę. Czy dogoni kolarza?
Jest jasne, że do rozwiązania zadania jest za mało danych, bo jeżeli do mety jest, powiedzmy 1 km, to oczywiście dzielny uciekinier wygra etap. Jeżeli do mety zostało 100 km, to nie ma szans. A zatem: jak daleko jest do mety, żeby peleton dogonił go na samym, samiutkim końcu, na samej linii? Też nie podam rozwiązania - polecam spróbować. A może jeszcze jest za mało danych?
Skąd jednak ten wątek cykliczny? To jasne! Piszę ten tekst w dniu zakończenia Igrzysk Olimpijskich w Tokio. Światek matematyczny obiegła kilkanaście dni przedtem wiadomość, że złoty medal w kolarstwie szosowym zdobyła Austriaczka, Anna Kiesenhofer, która "w cywilu" jest matematyczką. Przyjąłem tę wiadomość z pewnym lekceważeniem - mało to sportowców z fikcyjnym dyplomem? Ale ponieważ jednak znam się na tym, o czym piszę, zajrzałem do prac naukowych złotej medalistki (poprzedni medal w kolarstwie szosowym dla Austrii, wtedy jeszcze Austro-Węgier, zdobył w 1896 roku Felix Adolf Schmal).
Są to po prostu prace badawcze na dobrym poziomie naukowym, choć nie ma ich zbyt wiele. Spójrzmy na karierę naukową pani doktor: studia na Politechnice Wiedeńskiej, potem w Cambridge, doktorat w Kalifornii, a obecnie pracuje na politechnice w Lozannie. Nie tak źle, prawda? Na ogół sportowcy opowiadają nam o pełnym wyrzeczeń życiu: 300 dni w toku na zgrupowaniach, żeby rzucić dalej o pół metra, urwać pół sekundy, podźwignąć jeszcze jeden kilogram, dopracować do perfekcji ruch wiosła w wodzie. Nie oszukują - tak jest cena osiągnięć. Ale żeby tak wsiąść na rower w przerwie między rozwiązywaniem jednego równania i drugiego… i jeszcze wyprowadzić w pole rywalki? Przypomnę bowiem, że Anna Kiesenhofer uciekła tak, że pozostałe zawodniczki nie orientowały się, że jest ktoś przed nimi. Przy okazji zauważmy ciekawostkę językową: jeżeli kolarz ucieka, to znaczy, że atakuje!
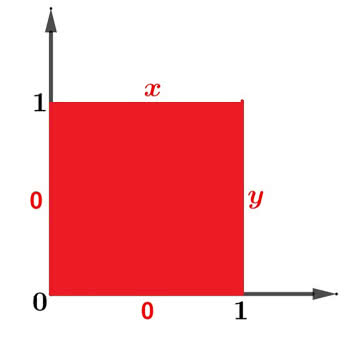
Mistrzyni olimpijska zajmuje się głównie half-vawe maps, co należy do równań różniczkowych cząstkowych. Ten przedmiot na studiach szedł mi wyjątkowo opornie - dostałem z niego tylko czwórkę z plusem, tym niemniej potrafię z bardzo grubsza ocenić prace z tej dziedziny. Niestety, nie potrafię napisać o wynikach Anny Kiesenhofer w sposób przystępny - do tego trzeba naprawdę być specjalistą w danej dziedzinie. Mogę tylko przytoczyć jedno z zagadnień, niezbyt dalekich od obszarów takich badań. Jest to efektowne równanie ciepłoprzewodnictwa, czyli jak ciepło rozchodzi się w danym ośrodku. Wyobraźmy sobie płytę o dowolnym kształcie - wygodnie będzie wziąć kwadrat (3)
Mamy daną temperaturę na obwodzie kwadratu, nie stałą, lecz opisaną pewną funkcją u. Załóżmy dla uproszczenia, że nie jest ona zmienna w czasie. Inaczej mówiąc, na obwodzie rozkład temperatury jest taki sam. Jaka jest temperatura w punktach wnętrza kwadratu? Na rysunku 3 lewa i dolna krawędź jest utrzymywana w temperaturze 0, a na pozostałych dwóch bokach rośnie proporcjonalnie.
Napiszę stosowne równanie, zdając sobie sprawę, że może być niezrozumiałe. Dwadzieścia pięć lat temu zrozumiałby to każdy uczeń liceum. Równanie to jest najsłynniejszym równaniem różniczkowym cząstkowym. Nazywane jest równaniem Laplace’a, na cześć markiza Pierre'a Simona de LaPlace (1749-1827). Kilka słów o tym wybitnym uczonym, nazywanym francuskim Newtonem. Urodził się w niezamożnej rodzinie, ale poznano się na jego zdolnościach do matematyki i fizyki i wobec tego zdobył porządne wykształcenie. Wniósł potem olbrzymi wkład do matematyki, mechaniki i fizyki. Wystarczy wspomnieć, że obliczył (tak, obliczył!) masę Saturna. Otrzymał wynik, różniący się od współczesnych pomiarów o jeden procent!
Współpracował z chemikiem Lavoisierem, który mocno zaangażował się w rewolucję francuską i po dojściu do władzy kolejnej frakcji rewolucyjnej został zgilotynowany, a wyrok uzasadniono, że "rewolucja nie potrzebuje uczonych". Może Laplace był zbyt wielki, może bardziej ostrożny. Został w 1806 roku (a więc za Napoleona) księciem, a w 1813 (czyli już po restauracji Bourbonów) markizem.
W fizyce i filozofii znany jest tak zwany demon Laplace’a. Jest to hipotetyczna istota, która zna położenia i prędkości wszystkich punktów materialnych świata. Ponieważ wszystko opisane jest i tak układem równań różniczkowych, taka istota może przewidzieć całą przyszłość. Wystarczy, by mogła rozwiązać ten układ. Tak czy owak - argumentował Laplace - przyszłość świata jest zdeterminowana. Co ma być, to będzie. Nie ma możliwości zmiany, bo wszystko to układ równań różniczkowych.
Procesy chemiczne (a więc i biologiczne) też. Nie wiem, czy to dobrze, czy źle, ale współczesna mechanika kwantowa powiada, że nie można znać jednocześnie położenia i pędu cząstki, a więc nic nie jest zdeterminowane. Ale demon Laplace’a odżywa w postaci poglądu, że może cały nasz Wszechświat to po prostu wielki komputer, który sam oblicza swoją przyszłość… Na pewno jednak Anna Kiesenhofer, kręcąc pedałami do mety olimpijskiej, nie myślała o swoich równaniach cząstkowych ani o tym, że według Laplace’a jej wygrana była i tak zapisana w Księdze Przeznaczenia (tzn. w układzie równań różniczkowych).
Wchodząc na kolejne piętro dygresji, wspomnę kilku dawnych mistrzów sportu, którzy mieli porządne wyższe wykształcenie. "Dawnych" - bo teraz dyplom zdobywa się nieporównanie łatwiej…, ale to już temat na inny artykuł. Było wśród tych sportowców wielu lekarzy. Był nim na przykład Roger Bannister (1929-2018, pierwszy człowiek, który przebiegł milę poniżej 4 minut, a było to 6 maja 1954; obecny rekord jest zaledwie o 16 sekund lepszy, 3.43,13 i jest niepobity od 1999 roku). Lekarzem był Stefan Lewandowski (1930-2007, najlepszy średniodystansowiec w Polsce w latach pięćdziesiątych XX wieku)… i inny Lewandowski (Zbigniew, 1930-2010), który był pierwszym Polakiem, który skoczył 2 metry wzwyż (12 maja 1957). Tak, rekord przedwojenny należał do Zbigniewa Pławczyka (1,96). Widocznie Lewandowski to takie sportowe nazwisko. Pierwsza zdobywczyni złotego medalu dla Polski po wojnie, Elżbieta Duńska-Krzesińska (1934-2015, skok w dal, Melbourne 1956, 6 m 35 cm), była dentystką.
Uzupełnię tę listę bokserem. Kazimierz Paździor (1935-2010, złoty medal w Rzymie w 1960 roku) był magistrem ergonomii. Przyjmujemy powszechnie, że matura sprzed 1939 roku to jakby magisterium z lat mniej więcej 1950-65 i habilitacja dzisiaj.
Uniwersyteckie wykształcenie ekonomiczne miała też najsłynniejsza polska lekkoatletka, Irena Szewińska (1946-2018) - widywałem ją na uczelni, bo studiowaliśmy w tych samych latach. Na ogół biegała po schodach. Była młodsza ode mnie o półtora miesiąca.
Wielu matematyków było dobrymi alpinistami, ale nie mam informacji, by w klasycznych sportach osiągali wybitne wyniki. Dopiero Anna Kiesenhofer. W prasie pisano potem, że sobie wszystko wyliczyła…
No, to wreszcie trochę matematyki, wróćmy do rysunku 3. Proszę się nie stresować, gdy przez chwilę nie będą Państwo rozumieć. Po chwili będzie znów nietrudno. A równanie Laplace’a nawet wygląda ładnie. Po lewej stronie mamy właśnie laplasjan, operator Laplace’a.
Taki wzór jest zrozumiały dla każdego z Czytelników, znających rachunek różniczkowy. Dla nich również pozostanie kwestią prostego sprawdzenia, że seria rozwiązań to funkcje 1, x, y, x2-y2, 2xy, x3-3xy2, 3x2y-y3, a ogólnym rozwiązaniem wielomianowym są: część rzeczywista i część urojona wyrażenia dla kolejnych n=0, 1, 2, 3, 4, …
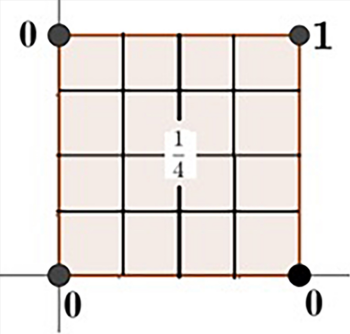
Ale można to równanie rozwiązać i tak. Temperatura w środku kwadratu jest średnią arytmetyczną temperatur w wierzchołkach. Zatem w środku kwadratu (3 i 4) mamy temperaturę
, średnia liczb 0, 0, 0, 1. Dzieląc dalej kwadrat na mniejsze oczka, wyznaczymy ją w każdym punkcie gęstej sieci - ale to tak, jakby w każdym punkcie.
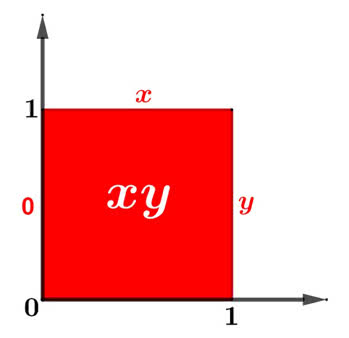
Dojdziemy do wniosku, że rozwiązaniem zadania, opisywanego rysunkiem 2, jest funkcja u=xy (5). Dla innych warunków brzegowych rozwiązanie może być bardzo skomplikowane, ale da się je otrzymać z wielomianów, które napisałem powyżej. Potem sprawa się bardzo komplikuje, wchodzi analiza harmoniczna, szeregi Fouriera i w ogóle matematyka z wysokiej półki, a wszystko ma zdecydowany kontekst praktyczny - fizyczny.
W pracach Anny Kiesenhofer pojawia się często geometria symplektyczna. Samo słowo "symplektyczny" jest ciekawe. Utworzył je jeden z najinteligentniejszych matematyków swoich czasów, Hermann Weyl (1885-1955). W słowie "complex", co po łacinie może znaczyć "spleciony razem" (mamy przecież w naszym kraju "szpitale zespolone"), zamieniamy łacińskie "co-" na greckie "sym-" i mamy sympleks, po angielsku symplectic, co wróciło do naszego języka jako "symplektyczny". O co jednak chodzi?
Można to przybliżyć tak. W tradycyjnej geometrii ważne są odległości punktów, kąty między liniami i pola figur. Przesunięcie i obrót nie zmienia cech figury: zachowuje ona ten sam obwód, te same kąty i takie samo pole. Ale są transformacje, które zmieniają i odległości, i kąty - ale nie zmieniają pola.
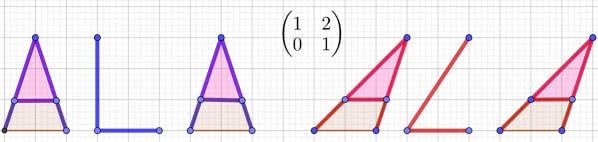
Na rysunku 6 widzimy odwzorowanie zachowujące pola figur. To zwykła kursywa, italiki. W stosunku do prostego druku górna część liter jest przesunięta o dwie jednostki (stąd liczba 2 w tablicy), dół się nie zmienia, a środkowe części przesuwają się proporcjonalnie.
W 1875 roku matematyk niemiecki Felix Klein sformułował tak zwany program z Erlangen. Narzucił on nam nowy topos geometrii. Topos to mniej więcej sposób, w jaki mamy myśleć o czymś, przez jakie okulary mamy spoglądać na świat. Od czasów Kleina mówimy, że geometria to badanie niezmienników grupy przekształceń. Przesunięcia i obroty zachowują długości, przekształcenia o wyznaczniku 1 (cokolwiek to znaczy) nie zmieniają pól, jeszcze inne nie zmieniają, powiedzmy, kątów. Znamy takie odwzorowania. Przypomnijmy sobie mapy w rzucie Mercatora. Ceną za wiernokątność jest deformacja okolic podbiegunowych - Grenlandia ma rozmiar Afryki, a Antarktyda ciągnie się przez całą mapę. Ale i taka mapa ma swoje zalety. W geometrii symplektycznej nie zmienia się jeszcze coś innego (a mianowicie forma różniczkowa skośnie symetryczna), ale to już temat na oddzielny artykuł.
Medal olimpijski jest okrągły jak koło opisane nierównością x2+y2≤r2, suma kwadratów nie większa niż kwadrat promienia. W geometrii symplektycznej często występuje różnica kwadratów x2-y2, a pani Annie Kiesenhofer potrzebny jest jeszcze jeden medal, żeby obydwa razem przypominały jej koła rowerowe.
Michał Szurek