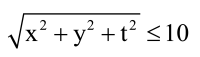Wycieczka w n-ty wymiar

Na początku zajęć o przestrzeniach wielowymiarowych pada zawsze pytanie: co jest tym czwartym wymiarem? Może czas? Odpowiadam, że może być nim cokolwiek. Jak to? Zobaczymy. Zrozumiałe, że potrzebna nam będzie pewna wyobraźnia. Oto ładny cytat:
- Najpierw trzeba szeroko rozpostrzeć skrzydła, potem pomachać ze trzy razy na próbę, żeby sprawdzić, czy wszystko w porządku, a potem….
- Ale ja nie mam skrzydeł - przerwał mu łoś.
- Aha - odrzekł zmieszany swoją nieuwagą kruk.
- Ale mam bogatą wyobraźnię. Może wystarczy, jak sobie wyobrażę, że mam skrzydła - dodał łoś bez kompleksów.
Joanna Haręża, Kruk między innymi, wydawnictwo AB, Warszawa 2005.
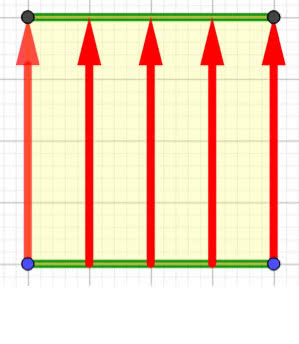
W młodości grywałem w tenisa. Kort trzeba było samodzielnie przygotować, w szczególności wyrównać. Służyła do tego płaska szczotka o szerokości 2 metrów, którą ciągnęło się za sobą. Należało dbać o to, by iść równo i miarowo. Jeżeli przyjmiemy, że szczotka była dwumetrowym odcinkiem, to po przejściu dwóch metrów zostawał na korcie wyszczotkowany kwadrat 2 na 2 metry. Można powiedzieć, że kwadrat powstaje przez przeciągnięcie odcinka w dodatkowym, drugim wymiarze. Bez użycia tradycyjnych oznaczeń x, y - zielony odcinek został przesunięty w czerwonym, prostopadłym kierunku.
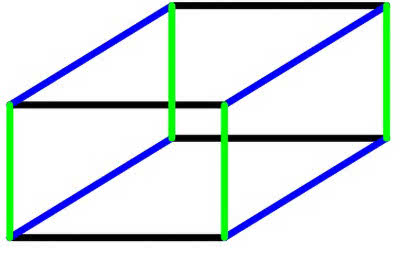
Podobnie zbudujemy sześcian. Trzeba przesunąć kwadrat w dodatkowym, trzecim wymiarze. Jeżeli jednak chcemy to narysować, mamy od razu kłopot. Co prawda nauczono nas w szkole rysunku w perspektywie. Przyjrzyjmy się w telewizji boisku piłkarskiemu. Wiemy, że na środku boiska jest koło (matematycznie: okrąg; przypomnę, że koło to pełna figura, a okrąg jest jej brzegiem), ale na ekranie jest elipsa. To nic, nasz mózg przetwarza ją na równy okrąg. Spójrzmy na rysunek 2. Możemy umówić się, że to też jest sześcian, bo to także tylko kwestia perspektywy. Widzimy, że czarno-niebieski kwadrat został przesunięty w prostopadłym, zielonym kierunku.
Nie wydaje się to bardzo odkrywcze. Ale to teraz, w XXI wieku. Gdy wiek XIX ledwo przekroczył połowę swojego stuletniego żywota (czyli w roku 1854), Bernhard Riemann wygłosił w Getyndze swój wykład habilitacyjny, O hipotezach, które leżą u podstaw geometrii (oryginalny tytuł niemiecki Über die Hypothesen, welche der Geometrie zu Grunde liegen). O samym tym wykładzie piękną książkę napisał ks. prof. Michał Heller, polecam!
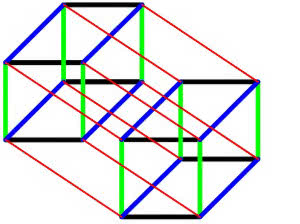
Riemann zmierzył się z zagadnieniami przestrzeni o większej liczbie wymiarów. Ówcześnie było to nie do pojęcia, nawet najwybitniejsi uczeni (jak na przykład Karl Friedrich Gauss) nie dopuszczali możliwości rozważania takich przestrzeni, a i samo podejście Riemanna też jest kręte. No, ale łatwo to pisać z dzisiejszego punktu widzenia, gdy wszystko zostało gruntownie opracowane, wyjaśnione, uproszczone i do końca zmatematyzowane. Spójrzmy na rysunek 3. Startujemy z dołu rysunku, z żółtej linii i idziemy przed siebie. Wszystkie możliwe drogi zamiatają coś, to jest wymiaru 2 - tak jak przy szczotkowaniu kortu. A więc możliwe drogi od n-wymiarowej figury A do innej figury, B, wypełniają figurę wymiaru n+1, o jeden większego.
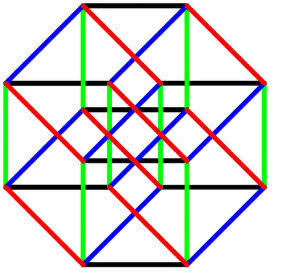
Wobec tego nic nie stoi na przeszkodzie, by zbudować "coś" wymiaru 4 - a raczej: narysować owo coś. Wybierzmy kierunek, który będzie na rysunku reprezentował czwarty wymiar (czerwony) i przesuńmy sześcian w tym wymiarze. Wynik widzimy na rysunku 4, a gdy postaramy się o ładny wykres, możemy dostać coś takiego, jak na rysunku 5. Oto przed Wami, drodzy Czytelnicy, bryła wymiaru 4 …, oj, oj, wcale nie bryła, tylko jej dwuwymiarowy rysunek. Sześcienny klocek możemy wziąć do ręki, naszej bryły… raczej nie. Ale co to szkodzi? Czyż nie mamy bogatej wyobraźni?
Inny pomysł potrzebny jest do stworzenia bryły mającej taki sam charakter, co trójkąt na płaszczyźnie i czworościan w przestrzeni. Myślmy o trójkącie równobocznym i czworościanie foremnym. Pierwszy z nich powstaje przez połączenie trzech punktów, położonych w tej samej odległości od siebie. Drugi - przez połączenie czterech punktów w przestrzeni, każdy z każdym. W następnym, czwartym wymiarze, jest równie prosto. Łączymy pięć punktów, każdy z każdym. Wszystkie mają być tak samo odległe od siebie wzajemnie. Dlaczego musimy uciec aż do czwartego wymiaru? Dlatego, że w trójwymiarowej przestrzeni takich pięciu punktów nie ma. Cztery tak, ale piątego nie ma już gdzie umieścić.
Wszystko da się wyrazić w nieskomplikowany sposób za pomocą współrzędnych. Trójkąt o współrzędnych przestrzennych (1,0,0), (0,1,0), (0,0,1) jest równoboczny - długość każdego z trzech boków wynosi . W przestrzeni wymiaru cztery mamy 4 współrzędne. Cztery punkty (1,0,0,0), (0,1,0,0), (0,0,1,0), (0,0,0,1) są odległe od siebie wzajemnie też o . Tworzą zwykły czworościan, piramidkę - tyle że leży ona w przestrzeni wymiaru 4. Pójdźmy wymiar wyżej - albo jeszcze dalej, nawet do wymiaru 100. Wyobrażamy sobie sto punktów. Pierwszy z nich ma współrzędne (1, 0,…,0) - zer jest 99. Drugi ma współrzędne (0,1,0,…0) - po jedynce następuje 98 zer, trzeci (0,0,1,0,…0) - z 97 zerami po jedynce, wreszcie setny ma 99 zer i jedynkę na końcu.
Z połączenia tych punktów powstaje bryła 99-wymiarowa o własnościach podobnych do trójkąta i czworościanu.
W wymiarach od 5 w górę jest jeszcze jedna bryła foremna - tworzą ją środki ścian kostki (tego odpowiednika sześcianu). Innych brył foremnych w tych wymiarach nie ma, ale - uwaga - w przestrzeni czterowymiarowej jest ich aż sześć. To też temat na oddzielny artykuł, a właściwie na duży wykład na poziomie uniwersyteckim.
Być może ktoś zaprotestuje: przecież czwartego wymiaru nie ma, żyjemy w trzech i wszystko to są tylko igraszki matematyczne. Zgodzę się z tym, że są to igraszki matematyczne. Ale…
Można przecież powiedzieć, że cała muzyka to tylko zabawa dźwiękiem, cała literatura to zabawa słowem, a malarstwo - to tylko kształty i kolory. A jednak wszyscy robimy to dla pewnej przyjemności, dla satysfakcji intelektualnej. Czyż nie tak? Czy nie wzrusza nas obraz, dobra książka, nastrojowa muzyka?
To wszystko byłoby za mało, jeśli chodzi o teorie matematyczne. Na szczęście matematyka jest nauką, którą spotykamy niemal wszędzie. Konkretnie: wszystko to ma zastosowanie, nie tylko w fizyce, ale na przykład w ekonomii. Przestrzenie wielowymiarowe spotykamy wszędzie…
Popatrzmy na rysunek 5 inaczej. Wyobraźmy sobie, że jest to sieć, sieć połączeń. Jakich połączeń? Wszystko jedno. Może to być sieć elektryczna, sieć kolejowa, informatyczna, kanałów wodnych, a nawet np. schemat wyciągów narciarskich. Przyjmijmy tylko jeden z wierzchołków jako początek (start, źródło, input itd.), a inny jako metę, koniec, ujście, output itd. Ja zdecyduję się na sieć kolejową. Lubię zadania "ruszają w dal pociągi dwa". Są naprawdę kształcące, a ja sobie dodatkowo wyobrażam, że wszystko dzieje się w jakimś odległym kraju, gdzie naprawdę istotne jest, gdzie i kiedy się one spotkają.
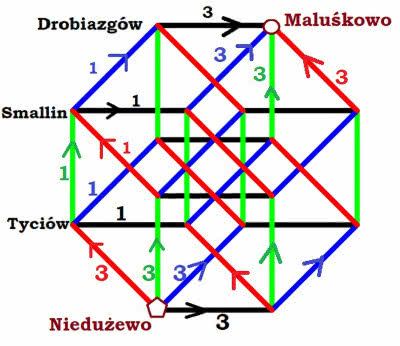
Spójrzmy na rysunek 6. Między Niedużewem a Maluśkowem jest gęsta sieć automatycznych połączeń kolejowych (wiem, że w Lille we Francji metro jest całkowicie zautomatyzowane - jeździ bez udziału człowieka; podobno w Warszawie też mogłoby tak być, ale przepisy nie pozwalają!). Każdy odcinek sieci ma przepustowość 1, to znaczy, że można nim wysłać jeden wagon na jedną jednostkę czasu. Jeżeli puścimy trzy wagony, będą one jechać trzy razy wolniej. Jaka jest przepustowość całej sieci?
Spójrzmy. Dyżurny ruchu w Niedużewie wysyła 3 wagony w każdym z czterech kierunków, a potem dzielą się one same. Niech jednostką czasu będzie 10 minut. A więc do Tyciowa dojeżdżają po 30 minutach trzy wagony. Dzielą się one po jednym i po dalszych dziesięciu minutach docierają do następnych stacji. W Smallinie spotykają się (ważne - w tym samym momencie) dwa wagony z dwóch różnych kierunków i każdy jedzie dalej. W Drobiazgowie spotykają się trzy wagony (jeden ze Smallina, drugi z południa, zieloną trasą i trzeci z południowego wschodu czerwoną). Znów: ważne jest, że dojeżdżają w tej samej chwili i wobec tego zgodnie ruszają już do końcowej stacji Maluśkowo.
Zbierzmy nasze obliczenia. Dwanaście wagonów w czasie 3+1+1+3=8, nie jest ważne, że to 80 minut. Chwila zastanowienia wystarczy, żeby zrozumieć, że przepustowość to 12 dzielone przez 8, czyli 1,5. W jakich to jednostkach? Trudno powiedzieć. Na wykładach mówię, że to w szurkach. Jeden szurek odpowiada jednemu wagonowi na jednostkowym odcinku.
W dydaktyce matematyki jest pojęcie zadań izomorficznych. To są zadania dotyczące różnych sytuacji, ale mające tę samą treść matematyczną. Nauczyciele szkół podstawowych znają te problem: jeżeli w klasie jest zadanie o cukierkach, a na klasówce będzie o czekoladkach, to dla części dzieci będzie to inne zadanie! Takiego podejścia nie pozbywają się niekiedy i studenci. Ale dla Czytelników jest zrozumiałe, że zamiast wagonów mogą w sieci przepływać prądy elektryczne, megabajty informacji, woda, narciarze na wyciągu, żołnierze… i tak dalej. Teoria przepływów w sieciach jest ważną gałęzią matematyki obliczeniowej.
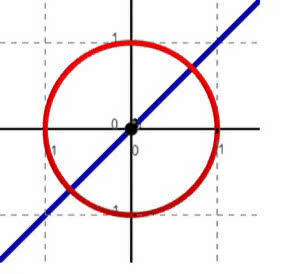
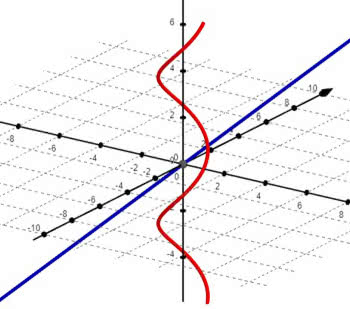
W pojęciu wymiaru ważniejsze jest co innego. Najpierw wyobraźmy sobie pusty plac, po którym jeżdżą samochody (nie wytłumaczę, po co jeżdżą - może po prostu tak sobie). Czy jeżeli dwa samochody znajdą się w tym samym punkcie, to mamy wypadek? Oczywiście, że… nie. Jeżeli przejadą przez to samo miejsce, ale w odstępie minuty, to wszystko będzie w porządku. To znaczy, że kolizja zdarzy się, gdy będą w tym samym punkcie czasoprzestrzeni (x, y, t). Proste, prawda? Przyjrzyjmy się wykresom przestrzennym. Samochód A jedzie ze stałą prędkością po niebieskiej linii prostej, zaś samochód B jeździ w kółko, jak na rysunku 7. Mogą się zderzyć, ale nie muszą. Zróbmy wykresy ich ruchu w czasoprzestrzeni (x, y, t). Wybrałem takie warunki początkowe, żeby krzywe przestrzenne nie stykały się. Jest bezpiecznie (rysunek 8) - chociaż naprawdę widać to dopiero na animacji albo po stosownych rachunkach. Zatem zadanie.
Zadanie. Wykazać, że krzywe (t, t, t) i (cos t, sin t, t) nie mają punktów wspólnych.
Rozwiązanie jest proste. Ma być t=sin t=cos t. Pierwsze z tych równań jest spełnione tylko dla t=0, ale cos 0=1. Punktu wspólnego nie ma.
Omówmy zatem kwestię bezpieczeństwa. Przyjmijmy, że bezpiecznie jest, jeżeli samochody są odległe o 10 metrów w przestrzeni albo o 10 sekund w czasie. Przypomnijmy sobie, jak mierzy się odległość w przestrzeni. Wystarczy nam wzór uproszczony - odległość punktu (x, y, t) od początku układu (0,0,0) to
Każdy samochód zatem roztacza wokół siebie swego rodzaju "kulę bezpieczeństwa". Kontroler ruchu może podejrzeć, czy dwie takie kule nie zahaczają o siebie. Wtedy powinien ostrzec kierowców o możliwej kolizji. Nie jest to jeszcze może powód do alarmu - sądzę, że powinien go ogłosić, gdy jeden samochód wejdzie w kulę bezpieczeństwa drugiego.
Samochody na pustym placu sobie jakoś poradzą, ale z samolotami w przestrzeni jest już inaczej. "Kula bezpieczeństwa" wokół nich jest już w przestrzeni czterowymiarowej (x, y, z, t) - ale tak naprawdę w przestrzeni o większej liczbie wymiarów, bo jej promień zależy również od prędkości, od pory dnia, od pogody i może od wielu innych parametrów. Pamiętam, że gdy latały jeszcze samoloty Concorde, nad lotniskiem paryskim było o włos od katastrofy: na kursie concorde’a pojawił się mały samolot w odległości 400 metrów. To kilka sekund lotu.
Dochodzimy tu do jednej z możliwości spojrzenia na wymiar, co to jest wymiar? Można powiedzieć, że jest to liczba parametrów potrzebnych do opisania pewnego zjawiska. Parametry te mogą, ale nie muszą być niezależne. Jeżeli są zależne, dostajemy do analizy skomplikowany obiekt geometryczny.
Napisałem, że to tylko jedna z możliwości. Inna prowadzi nas do fraktali - figur, które mają wymiar niecałkowity, na przykład nie 1, nie 2, coś pośrodku. Jak to jest możliwe? Punktem wyjścia jest taka oto obserwacja. Jeżeli powiększymy długość boku kwadratu dwukrotnie, to pole tego kwadratu wzrośnie czterokrotnie (rysunek 9), a jeżeli potroimy bok, to pole wzrośnie aż 9 razy. Dla sześcianu idzie to jeszcze szybciej: zwiększenie długości krawędzi dwukrotnie spowoduje ośmiokrotny wzrost objętości, a potrojenie - wzrost 27-krotny. W czwartym wymiarze zależność ta zmienia się wraz z czwartą potęgą, w piątym - z piątą.
Z ciekawości przyjrzymy się wymiarowi 10. O ile trzeba zwiększyć krawędź kostki dziesięciowymiarowej, żeby podwoiła się objętość? To proste: , czyli w przybliżeniu 1,07. Siedmioprocentowy wzrost krawędzi podwaja objętość. Ale to jest także zadanie z ekonomii. Jeżeli inflacja roczna w kraju wynosi 7%, ceny podwajają się po 10 latach.
Urodzony w Polsce Benoit (=Benedykt) Mandelbrot (1924-2010) wprowadził do matematyki figury o ułamkowym wymiarze. Jak to jest możliwe? Właśnie przez analogię z powiększaniem kwadratu i sześcianu. Mówimy, że wymiarem figury jest n, jeżeli można ją podzielić na takie kn części, że każda z nich jest podobna do wyjściowej w skali 1:k. Taka liczba n nie musi być całkowita. Tak jest właśnie dla fraktali (nazwa od łacińskiego fraktus = złamany). Fraktale są "modne", przy kilku okazjach gościły i na naszych łamach. Nie będę więc o nich pisać. Kto nie miał okazji się z nimi zetknąć, może w wyszukiwarce wpisać stosowne słowo i wyskoczą tysiące stron. Jednym z ostatnich pomysłów Mandelbrota było zastosowanie fraktali i tak zwanych quasi-fraktali do opisu zjawisk giełdowych. Zastosowania matematyki do gry giełdowej traktuję z dużą podejrzliwością - przypomina mi to odróżnianie banknotów prawdziwych od fałszywych na podstawie popiołu, który powstaje po ich spaleniu.
O ciekawej, "prawdziwej" geometrii figur wymiaru 4 i wyższych - to już innym razem.
Michał Szurek