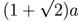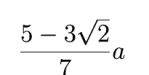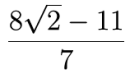Symetrie i coś w tym stylu. Dlaczego rak chodzi wspak? Bo jego ojciec chodził tak!
Turystom i narciarzom górskim znane jest zjawisko inwersji pogodowej: zdarza się, że w dolinach jest zimnej niż na szczytach. To zrozumiałe – zimne powietrze spływa w dół i jeżeli nie ma wiatru, to utrzymuje się tam. Natomiast na ogrzewanych słońcem szczytach jest miło i przyjemnie.
Redaktorom znany jest tak zwany czeski błąd, polegający na przestawieniu liter: Wraszawa, Karków, kordła. Istotnie, w naszych podobnych językach to zjawisko jest dość częste, na przykład szewc to po czesku švec. Kto z Czytelników uczył się algebry liniowej, pamięta może nieprzyjemne zadania obliczeniowe: wyznacz macierz odwrotną do podanej. Jest to istotnie trudne zadanie, proste algorytmy działają w czasie proporcjonalnym do sześcianu rozmiaru macierzy. Znaczy to, że przy dwukrotnym zwiększeniu rozmiaru macierzy złożoność obliczeniowa rośnie ośmiokrotnie.
Na lekcjach matematyki w szkole mamy permutacje, a w nich inwersje. Jeżeli w permutacji (czyli ustawieniu liczb) większa stoi przed mniejszą, to mówimy, że ta para tworzy inwersję. Na przykład gdy ustawieniem jest 1 2 4 5 3, to mamy dwie inwersje: pary 4–3 i 5–3. Inwersje mamy w chemii, biologii i psychologii.
W retoryce inwersja zwana jest też szykiem przestawnym. To inna kolejność słów, niezgodna z kanonem gramatyki. Używana jest często w poezji, dla wzmocnienia nastroju. W normalnym liście napisalibyśmy do przyjaciela, że chcemy wrócić do leśnych pagórków i zielonych łąk, ale o ile bardziej porusza nas tęsknota poety:Do tych pagórków leśnych do tych łąk zielonych,
Szeroko nad błękitnym Niemnem rozciągnionych.
Wiemy, że lustro odwraca lewo i prawo. Możemy się zastanawiać, dlaczego nie odwraca góry i dołu. Ale odwraca! Połóżmy lustro na podłodze i stańmy na nim. Zobaczymy, że „ten drugi” wisi głową w dół. Z odwracaniem trzeba w ogóle uważać. Popularny dawniej tygodnik „Przekrój” publikował „humor z zeszytów szkolnych”. Zapamiętałem jeden z nich:
Gospodyni doiła krowę nad rzeką, a w wodzie było widać odwrotnie.
Leonardo da Vinci zapisywał swoje notatki pismem lustrzanym; być może po to, by utrudnić ich przeczytanie.
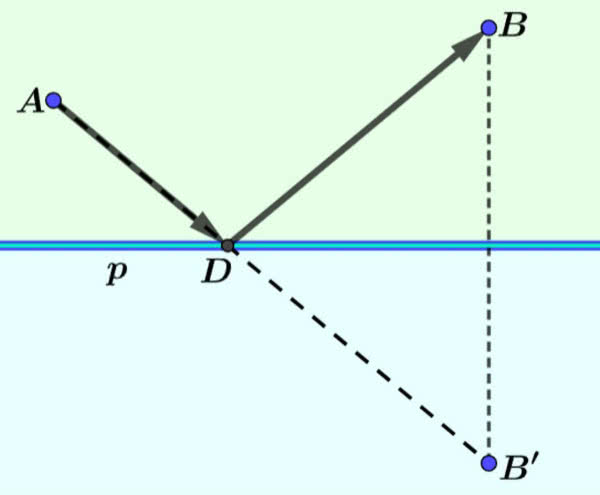
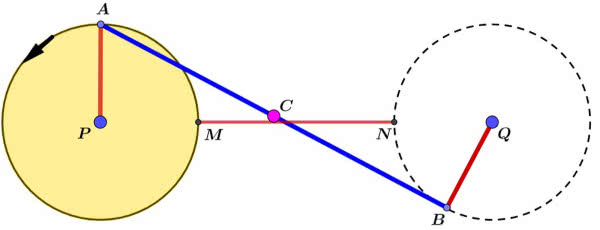
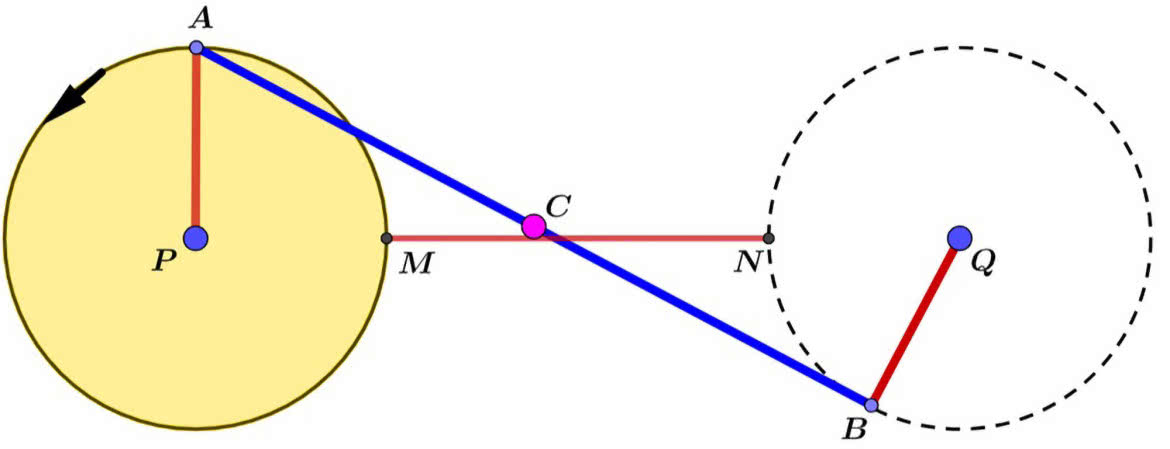
Bardzo częstym motywem z lustrem w geometrii są zadania o najkrótszej drodze. Chcemy dostać się z A do B, ale tak, by dotknąć jeszcze prostej p – niech na przykład ta prosta będzie rzeką, w której chcemy napoić konia. Rozwiązanie jest znane (1). Odbijamy symetrycznie punkt docelowy i korzystamy z tego, że najkrótsza droga między dwoma punktami biegnie po linii prostej.
Możemy to rozumowanie zwielokrotnić.
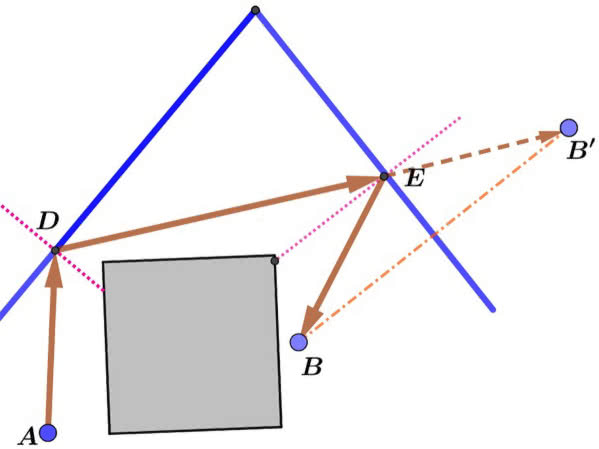
Na rysunku 2 mamy rozwiązanie zadania o odbiciu w dwóch zwierciadłach: chcemy oświelić punkt B latarką umieszczoną w A. Niestety, przeszkoda umieszczona między A i B uniemożliwia oświetlenie bezpośrednie. Możemy jednak skorzystać z dwóch zwierciadeł. Kierujemy zatem promień na punkt D, w nim następuje odbicie do E, a w nim już do B.
Odbicie zwierciadlane stosujemy w wielu zagadnieniach związanych z szukaniem najkrótszej drogi. Oto ładne zadanie na szukanie minimum.
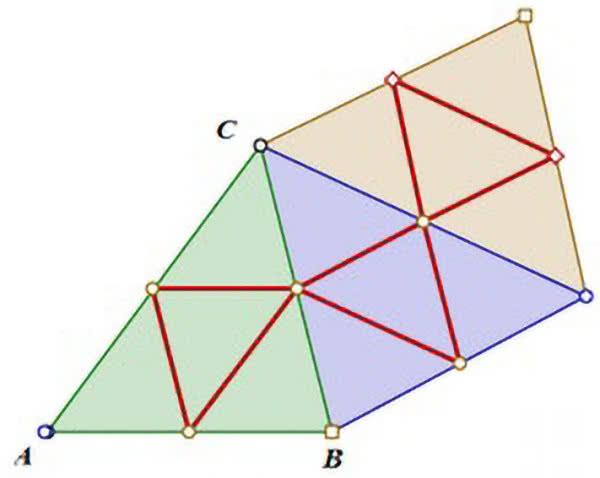
W trójkąt ostrokątny wpisać trójkąt o najmniejszym obwodzie.
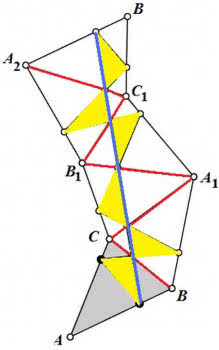
Odpowiedź. Trójkątem o najmniejszym obwodzie, wpisanym w dany trójkąt ostrokątny, jest trójkąt ortyczny – utworzony przez spodki trzech wysokości. Fascynujący, „fizyczny” dowód widzimy na rysunku 3 i 4. Zaznaczmy na bokach trzy punkty i odbijmy nasz trójkąt symetrycznie, po kolei w każdym boku, jak to sugeruje rysunek 4. Tylko przy trójkącie ortycznym odbite odcinki ustawią się w jednej linii prostej, najkrótszej.
***
Z pewnego punktu widzenia linia prosta jest przeciwieństwem okręgu. Tu prosto – tam krzywo. Na stadionie lekkoatletycznym mamy na przemian proste i łuki. Na szosie jest inaczej, łuki nie zawsze są fragmentami okręgu.
Wiele jest prawdy w tym, że najgenialniejszym urządzeniem technicznym jest koło. Efektywny transport na dużą skalę jest nie do pomyślenia bez niego, choć i ono ma wadę: wymaga w miarę gładkiej drogi. Może dlatego koła nie znali Indianie z Ameryki Południowej, zamieszkujący tereny górzyste.
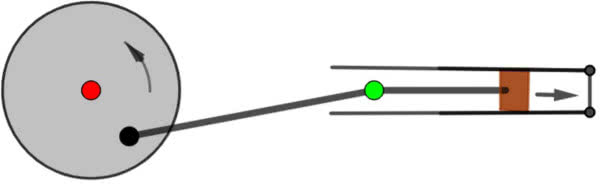
W samych początkach ery przemysłowej pojawiło się zadanie zamiany ruchu prostoliniowego na obrotowy (bądź odwrotnie). Dobrze służy temu zaprojektowane w 1782 roku przez wynalazcę maszyny parowej, Jamesa Watta, urządzenie z trzech prętów (5). Przymocowane są w punktach P i Q i połączone przegubowo w A i B. Gdy punkt A porusza się po okręgu, to ciągnie za sobą B. Środek odcinka AB porusza się wtedy tam i z powrotem; wprawdzie nie idealnie po odcinku MN, ale „prawie”. Torem jego ruchu jest krzywa w kształcie ósemki – zwana właśnie krzywą Watta, ale bardzo spłaszczona, na tyle, że może być to podstawą do zastosowaniach w technice.
Oparte na tym samym pomyśle urządzenie jest dziś powszechnie stosowane (6). Matematyczną niedoskonałość konstrukcji z powodzeniem rekompensują smary.
Ale urządzenie zamieniające dokładnie ruch obrotowy na posuwisty (i odwrotnie) znane było już Kopernikowi. Wspomniał o nim w swoim dziele O obrotach ciał niebieskich. Gdy koło o promieniu r toczy się wewnątrz koła o dwa razy większym promieniu (czyli 2r), wówczas wybrany punkt mniejszego koła porusza się tam i z powrotem po średnicy większego koła. Widziałem kilka zabawek, w których wykorzystuje się tę własność kół, ale przenoszenie większych sił w ten sposób jest technicznie niepraktyczne i dlatego nie znalazło zastosowania.
Matematycznie dokładne rozwiązanie problemu daje inwersor Peaucelliera, wynaleziony przez francuskiego oficera marynarki w 1864 roku, gdy matematycy już poszukiwali dowodu, że takiego mechanizmu nie ma.
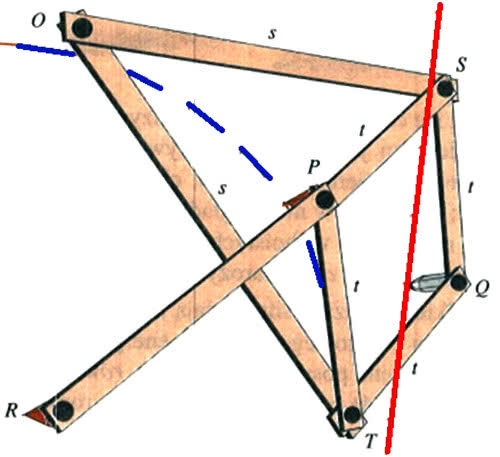
Urządzenie Peaucelliera jest bardzo proste. Składa się z siedmiu prętów, połączonych przegubowo (7). Cztery z nich mają jednakową długość t, dwa inne długość s, siódmy dowolną. Mocujemy urządzenie w dwóch stałych punktach O i R tak, by OP=OR. Widzimy równoległobok.
Gdy punkt P w inwersorze Peaucelliera zakreśla łuk okręgu o promieniu |PR| wokół punktu R, to punkt Q porusza się po linii prostej.
***
Zadanie o zamianie prostej na okrąg i odwrotnie przypomina starożytne zadanie Apoloniusza z Pergi (przybliżone daty życia 262–190 p.n.e.). Istotnie, to on pierwszy je rozwiązał.
Zadanie Apoloniusza. Skonstruować okrąg styczny do trzech danych.
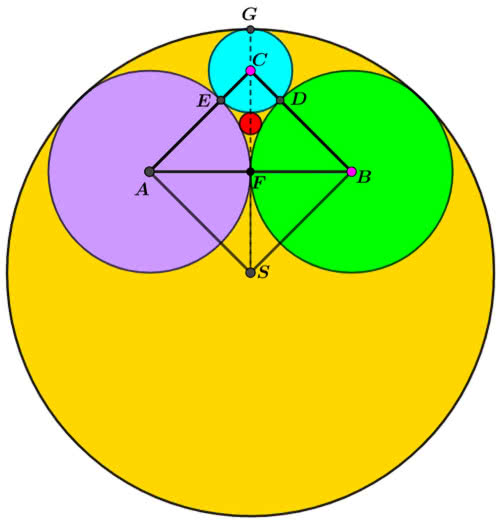
Okręgów takich może być nawet osiem i można je ponumerować, używając układu dwójkowego. Jeżeli przez 0 oznaczymy styczność wewnętrzną, a przez 1 – zewnętrzną, to w ogólnym przypadku mamy 23=8 możliwości: 000, 001, 010, 011, 100, 101, 110, 111. Odpowiadają one, jak widzimy, liczbom od zera do 7, w zapisie dwójkowym.
Na rysunku 8 oprócz „małego” i „dużego” okręgu stycznego do trzech danych (000 i 111) widzimy trzy okręgi typu „dwie jedynki + jedno zero” i „dwa zera + jedynka”.
Swoją drogą, rysunek 8 przypomina mi sieć rozjazdów w jakimś ważnym węźle kolejowym.
***
Zadanie Apoloniusza o konstrukcji stycznych ma zatem 2200 lat i wydawać by się mogło, że już niczego nowego z nim nie da się wymyśleć. Ale w XXI wieku przyrost wiedzy przyspiesza… coraz szybciej. Mnie to bardziej niepokoi, niż cieszy. Ja sam, będąc przecież specjalistą, zdziwiłem się, jak bardzo zagadnienie Apoloniusza rozrosło się na wyższe wymiary, większe wielokąty i inne obiekty zamiast okręgów. Surfując po sieci, znalazłem bardzo ładny, „nowiutki” sposób konstrukcji okręgu stycznego do trzech danych. Matematycy cenią ładne, pomysłowe i abstrakcyjne rozumowania, które nie tylko prowadzą do dowodu twierdzenia, ale dają do myślenia – podobnie jak kontemplacja dzieła sztuki.
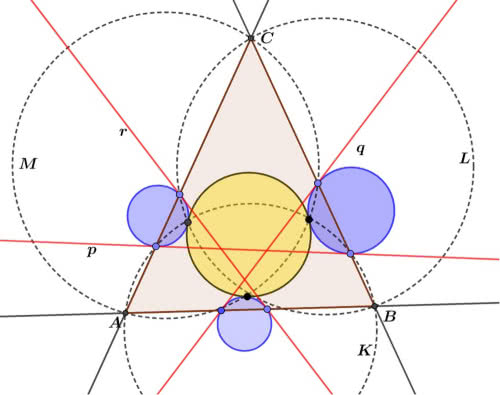
Oto konstrukcja okręgu Apoloniusza. Zdziwiłby się, gdyby ją zobaczył (9).
Rysujemy trzy wspólne styczne p, q, r danych okręgów. Łącząc punkty styczności, otrzymujemy trójkąt ABC. Prowadzimy trzy okręgi K, L, M przez wierzchołki trójkąta i punkty styczności. Punkty przecięcia tych okręgów wyznaczają trzy punkty na okręgu, który będzie styczny do trzech danych.
***
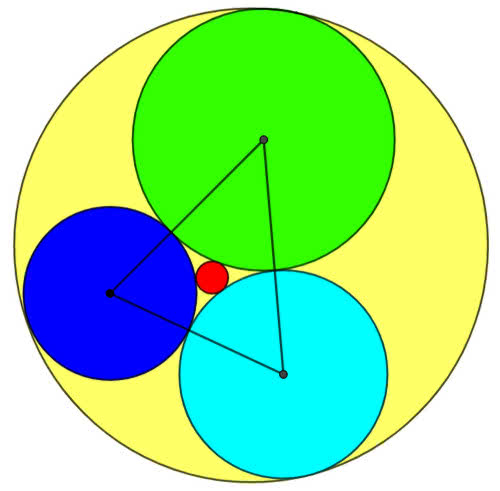
Gdy trzy okręgi są już wzajemnie styczne, to styczne do nich nazywane są też okręgami Soddy’ego. Frederic Soddy (1877–1956) był brytyjskim chemikiem, laureatem Nagrody Nobla w roku 1921 za badania związków radioaktywnych oraz pochodzenia i charakteru izotopów. W 1936 roku opublikował na łamach czasopisma „Nature” artykuł o właśnie takiej konfiguracji okręgów, pod żartobliwym tytułem The kiss precise i z wierszem na ten temat. Podobno napotkał ten układ w swojej pracy chemika, ale nie dotarłem do szczegółów. Z tego całkiem długiego wiersza przytaczam jedną zwrotkę i (własne) tłumaczenie:
Four circles to the kissing come
The smaller are the benter
The bend is just the inverse of
The distance from the centre.
Kółka chcą buzi sobie dać.
Co w nich się musi zmienić?
Krzywizny, czyli (masz to znać!)
Odwrotność ich promieni!
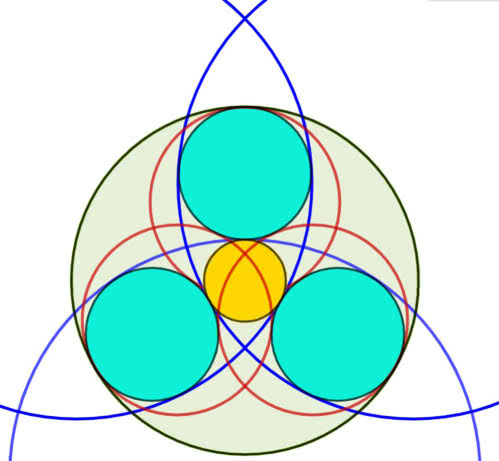
Interesująco wygląda konfiguracja Soddy’ego dla trójkąta prostokątnego równoramiennego (11). Jeżeli ramiona trójkąta ABC mają długość a, to okrąg zewnętrzny okrąg Soddy’ego ma promień
a wewnętrzny
Stosunek tych dwóch wielkości jest równy
Przy zagadnieniu Soddy’ego znowu daje o sobie znać „urok odwrotności”. Formułę wiążącą promienie czterech okręgów w tej konfiguracji są dane skomplikowanym wzorem, ale gdy zamiast promieni r1, r2, r3, r4 weźmiemy ich odwrotności, to wzór – będzie całkiem ładny. Dla styczności zewnętrznych mamy bowiem:
2(k12 + k22 + k32 + k42) = (k1 +k2 + k3 + k4)2
Dla styczności zewnętrznych zastępujemy w tym wzorze niektóre plusy minusami. Zależność tę Harold Scott MacDonald Coxeter, kanadyjski matematyk (1907–2003), jeden z najlepszych geometrów XX wieku.
Michał Szurek