Problem Józefa Flawiusza

Legenda mówi, że po klęsce powstania Ben Matatia (a więc późniejszy Flavius) schronił się do jaskini wraz z pozostałymi jeszcze 40 żołnierzami. Powstańcy postanowili się raczej wzajemnie pozabijać, niż oddać w niewolę. Flawiusz próbował ich od tego odwieść, ale perswazje nie odnosiły skutku. Zaproponował tylko ścisły porządek w egzekucjach. Ustawił wszystkich, wraz z sobą, w krąg i liczył: „raz, dwa, trzy”. Każdy, na kogo wypadła trójka, był zabijany. Sam jednak siebie ustawił tak, by być ostatnim w tym makabrycznym procederze. Podobno zresztą kilku ostatnich żołnierzy też postanowiło się poddać.

Tyle legenda sprzed dwudziestu wieków. Zadanie matematyczne, jakie się z nią wiąże, jest jasne: jak wyznaczyć to szczęśliwe miejsce? Nie jest to bardzo trudne. Ale matematyka różni się od łamigłówek szukaniem ogólnych rozwiązań i szerszym podejściem do problemu. Konkretnie: chcielibyśmy od razu mieć algorytm rozwiązania podobnego zadania przy innych danych: inna liczba żołnierzy, powiedzmy n, i eliminowany nie co trzeci, a co k-ty.

Przepiszę fabułę, z tragicznej na pozytywną. Lepiej będzie się nam wszystkim myślało. Otóż w dalekim królestwie Fioletonii panował król Fijołek Pierwszy. Miał on ukochaną i śliczną córkę, której oficjalnym imieniem było Violetta, ale dla wszystkich była księżniczką Fiołkinią. Była ona nie tylko piękna, ale i mądra. W szczególności nie było nikogo, kto by jej dorównał w matematyce. Nawet stary alchemik królewski, Fiolemon, nie nadążał za nią z całkowaniem.

Gdy Fiołkinia osiągnęła wiek dojrzały, król postanowił wydać ją za mąż, oferując zresztą w posagu pół królestwa i pół niemałego majątku. Jak wiemy z literatury, królowie często tak robią. Nic dziwnego, że zgłosiło się wielu młodych kawalerów, a i podstarzałych wdowców nie brakowało. „Los wskaże ci męża” - oświadczył król Fijołek. Ale, jak to również często bywa, Fiołkinia miała już ukochanego - dzielnego Fiorenza. Już dawno temu przysięgali sobie miłość.

Król był jednak staroświecki i nie dał się przebłagać. Z pomocą przyszedł alchemik Fiolemon - król bowiem zwierzył mu się ze swojego pomysłu. Stary alchemik bardzo kochał księżniczkę i chciał, by była szczęśliwa. Przyszedł wieczorem do pokoju zapłakanej Fiołkinii. „Nie mogę ci pomóc, córuchno. Król powiedział, że ustawi wszystkich kandydatów w koło i będzie odliczać: raz, dwa, trzy. Na kogo wypadnie trójka, ten odjeżdża do domu. Kto zostanie ostatni, ten weźmie cię za żonę. Sama widzisz, że ślepy los wybierze ci małżonka. Żal mi ciebie, naprawdę mi żal. Może weźmiesz mnie do siebie, żebym ci służył i doradzał w twoim nowym domu?” 

– A ilu jest starających się?
– Kochana ty moja, czterdziestu jeden.

Królewna przestała płakać i  rzuciła się staremu na szyję.

– Dzięki ci, mój wierny i poczciwy mędrcze. Dalej to już sama dam sobie radę. To musi być łatwy algorytm. Do rana na pewno znajdę rozwiązanie!

I rzeczywiście, jakoś tak się stało, że spośród czterdziestu jeden kandydatów do ręki królewny (a także, czego nie należy lekceważyć, do połowy królestwa) „los” wskazał Fiorenza. Słowo królewskie jest prawem, zatem niebawem połączono Fiorenza i Fiołkinię węzłem małżeńskim. Jak to zwykle bywa w takich historiach, żyli potem długo i szczęśliwie - a z pieniędzy otrzymanych w posagu założyli Akademię Matematyczną i fundowali stypendia młodym uczonym.

***

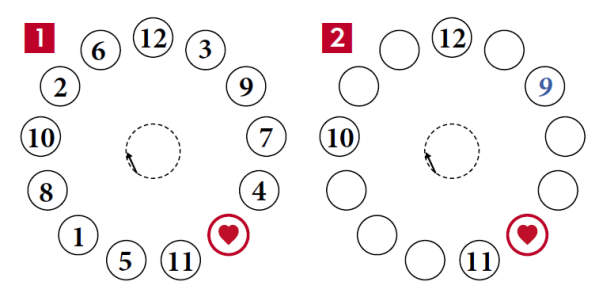
Być może Fiołkinia po prostu liczyła od tyłu. Dla większej czytelności przyjmijmy, że starających się było mniej, powiedzmy, trzynastu. Narysowała trzynaście kółek i w jednym z nich umieściła Fiorenza. Następnie liczyła, zaczynając od następnego: raz, dwa, trzy i usuwała tego trzeciego. Numerki na rysunku 1 wskazują kolejność, w jakiej konkurenci byli usuwani. Rysunek 2 pokazuje, co się dzieje po usunięciu dziewiątego. Liczymy: Firenzo = raz, jedenasty = dwa, dziesiąty = trzy i odpada. Liczymy dalej: dwunasty = raz. Firenzo = dwa, jedenasty = trzy i odpada. Zostaje dwóch: Dwunasty i Firenzo. Liczymy dalej: dwunasty = raz, Firenzo = dwa, dwu-nasty = trzy. Odpadłeś, Dwunasty, na samym końcu.

A zatem, gdyby n=13, należałoby tylko skłonić króla, żeby zaczynał liczenie od tego, który stoi zaraz za Firenzem. Królewna (albo alchemik Fiolemon) na pewno daliby radę przekonać króla (prośbą, odwróceniem uwagi albo podstępem), żeby tak właśnie zaczął… A jak było naprawdę, to znaczy gdy Firenzo miał aż 40 konkurentów, zobaczymy potem.

***

Weźmy się do matematyki. Najpierw przypatrzymy się zagadnieniu, gdy odrzucany jest nie co trzeci, a co drugi kandydat. Tu matematyka jest ciekawsza. Postąpimy odwrotnie niż Fiołkinia - bardziej algorytmicznie. Zaczynamy od numeru 1 albo od litery A; na rysunkach umieszczanej u góry. Chcemy wyliczyć numer szczęśliwego miejsca.

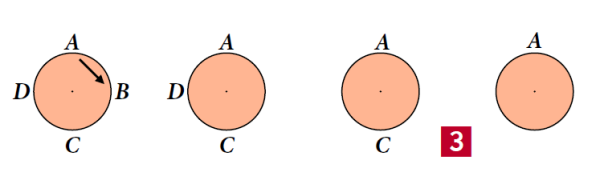
Zaczniemy analizę od n=4; to znaczy od czterech starających się. Zaczynamy od górnego i odliczamy w prawo, w kierunku obrotu wskazówek zegara (3). Mamy więc A=1.

Na kandydata B przypada „dwa” - żegnamy go. Potem znów „jeden” na C i „dwa” na D. Zostają A i C, ale znów „jeden” to  A, no a  „dwa” to C. Wygrywa A. Jeżeli A=1, B=2, C=3, D=4, to widzimy, że najpierw odpadają dwie parzyste. Sformułujmy to tak: gdy n=4, to wygrywa numer 1.

Podobnie będzie dla ośmiu kandydatów (4). Mamy tu interesujące rozumowanie, zwane przez informatyków rekursją bądź (niegodnie z duchem polszczyzny) rekurencją. Sprowadzamy zadanie do poprzedniego. Najpierw odpadną parzyści. Zostanie czterech. Ale wiemy, że dla czterech wygrywa pierwszy, zatem i dla ośmiu wygrywa pierwszy. Inaczej mówiąc: ten górny, jedynka, ten, od którego król zaczyna.

Przejdźmy od 8 do 16. Widzimy, że będzie tak samo. W pierwszej turze odpadną parzyści, a do drugiej przejdzie ośmiu, z nadzieją na dalsze szczęście w procedurze. Ale przed chwilą przekonaliśmy się, że w tej sytuacji (n=8) wygrywa pierwszy - górny. A zatem i dla n=6 rękę królewny weźmie numer 1. Trochę to przypomina system pucharowy rozgrywek, zwany teraz „fazą play off”, czyli w którym przegywający od razu odpada. Sympatykom Igi Świątek i Huberta Hurkacza znana jest „drabinka turniejowa” - stosowana również na przykład w mistrzostwach świata w grach zespołowych, od poziomu ćwierćfinałów albo jeszcze wcześniej. Może tak będzie wyglądać tabela pewnych mistrzostw?

Wracamy do zagadnienia Flawiusza - a dla nas problemu Fiorenza i Fiołkonii. Wydaje się, że zadanie jest już rozwiązane: trzeba się ustawić na pierwszym miejscu. Niestety, to nie jest tak. To jest prawdą tylko wtedy, gdy liczba kandydatów jest potęgą dwójki. Zobaczmy na przykład, co dla n=5. Starają się Alkopój, Barnaba, Częstomir, Drabowit i Elektrycjusz. Przypiszmy im numery od 1 do 5. Już na początku odpada Barnaba, nr 2. Zostaje czterech i odliczanie zaczyna się od Częstomira, nr 3. Ale widzieliśmy, że gdy mamy czterech współzawodników, to wygrywa ten, od którego zaczyna się odliczanie. Gdyby było tylko pięciu chętnych, a król odliczałby „co 2”, to wygrałby numer 3. 

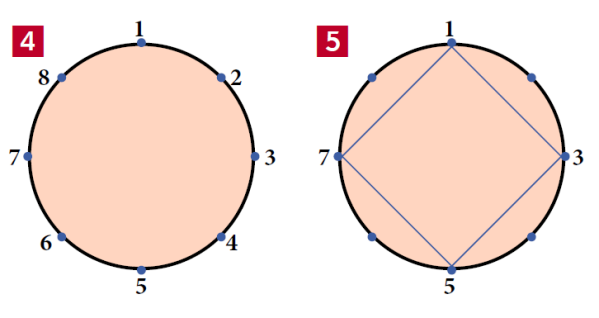
Ogólną prawidłowość zgadniemy po jeszcze jednym przykładzie. Niech kandydatów będzie sześciu (8). Niech ten szósty nosi nowoczesne imię Flamaster.

Jak zawsze, najgorsze jest miejsce drugie, bo liczymy „raz, dwa” i dwójka jest pierwszym przegranym. Zostaje pięciu i zaczynamy liczenie od tego z trójką. Ale przed chwilą ustaliliśmy, że gdy kandydatów jest pięciu, to wygrywa ten, który jest na trzecim miejscu za początkowym. Jest to zatem piąty kandydat, Elektrycjusz. Co będzie, gdy starających się będzie siedmiu, a zatem, gdy do wyliczonych dojdzie jeszcze Grzmisław? Zobaczmy. Barnaba odpada od razu. Zostaje sześciu: oprócz Alkopoju jeszcze Częstomir, Drapowit, Elektrycjusz, Flamaster i Grzmisław. Liczenie zaczyna się od Częstomira. Z  rozpatrywanego przed chwilą przypadku n=6 widzimy, że  wygrywający jest ten, kto stoi cztery miejsca za Częstomirem. Jest to Grzmisław, numer 7.

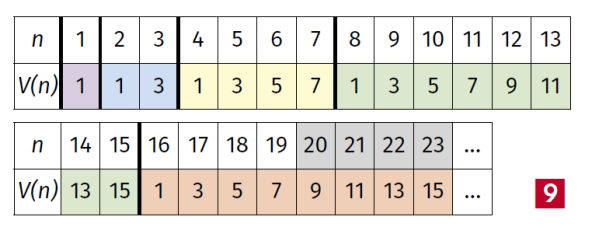
Wszystko razem układa się w ciekawą tabelkę. Jeżeli oznaczymy przez V(n) numer miejsca, na którym powinien stanąć ukochany Fiołkinii, gdy jest n kandydatów, to mamy:

Ciąg liczb nieparzystych jest zawsze ciekawszy niż parzystych. A dane z tabelki na rysunku 9 można ująć takim oto wzorem matematycznym:

Jeżeli n=2^k+m, to V(n)=2m+1; przy czym wykładnik k jest taki, że 2^k≤n<2^k+1.

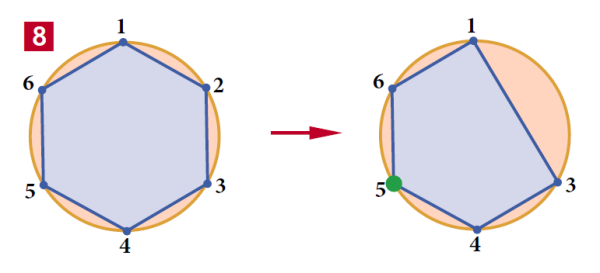
Zobaczmy, na którym miejscu powinien stanąć pełen nadziei Firenzo, gdyby miał 40 konkurentów, aby przy odliczance króla padło właśnie na niego. Mamy 41=32+9=2⁵+9, zatem V(n)=2∙9+1=19.

To wszystko staje się jeszcze dziwniejsze, gdy przejdziemy do… układu dwójkowego. Przedstawmy liczby 19 i 41 w tym układzie:

41₂=32+8+1=2⁵+2³+2⁰=101001, 19₂=10011.

Co ma 101001 do 10011?
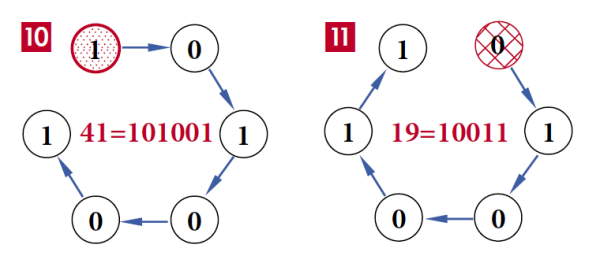
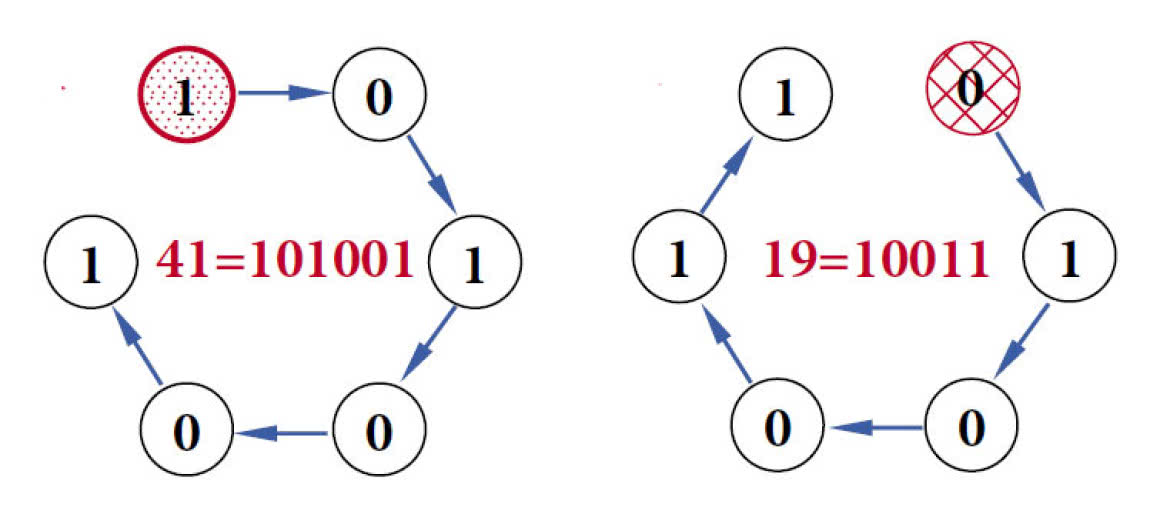
Zobaczmy na rysunkach 10 i 11:

Obracamy 41 i „wychodzi” 19. Można to ująć ogólnie: V(n) to n z cykliczną zamianą bitów. Ciekawe, czy Józef Flawiusz zdawał sobie z tego sprawę? Może i tak, bo starożytni uczeni byli naprawdę mądrzy.

***

Wróćmy do oryginalnego zagadnienia Flawiusza (a raczej królewny Fiołkonii). Król odlicza do trzech i co trzeciemu daje czarną polewkę. Na marginesie zauważmy, że jeżeli starających jest 41, to trzeba wydać 40 porcji zupy. Ale to już zmartwienie rządcy i kucharza. Można dojść do rozwiązania w podobny sposób, jak dla odliczania po dwa albo metodą Fiołkonii liczenia do tyłu. Tu obliczenia są dłuższe, matematyka staje się trudniejsza, ale wynik jest równie, a może nawet jesz-cze bardziej ciekawy niż dla odliczania co dwa. Otóż rządzi tym tajemniczy ciąg, zaczynający się tak: 

1, 2, 3, 5, 8, 12, 18, 27, 41, 62, 93, 140, 210, 315, 473, 710, 1065, 1598, 2397, 3596, 5394, 8091, 12137, 18206, 27309, 40964, 61446, 92169, 138254, 207381, 311072, 466608, 699912, 1049868, 1574802, 2362203, 3543305, 5314958, 7972437, 11958656, …

Każdy jego wyraz jest równy półtora poprzedniego (z ewentualnym zaokrągleniem do góry). Na przykład po 5 następuje siedem i pół, co zaokrąglamy do ośmiu.

Królewna: Ojcze, ilu jest absztyfikantów?
Król: Nawet nie liczyłem. Ale tylko jeden zostanie twoim mężem. Ten, na którego los padnie.

Królewna (szeptem do alchemika). Dowiedz się, ilu ich jest, idź do Firenza i powiedz mu, niech szybko obliczy, na którym miejscu ma stanąć. Jeżeli jest ich n, to ma z tego ciągu wybrać najmniejszą liczbę d_n większą niż 2n i stanąć na miejscu 3n+1–d_n. Co mówisz, Fiolemonie? Że jest ich 41? Świetnie. Najmniejsza liczba z tego ciągu większa od 82 to 93. Jeżeli naprawdę mnie kocha, to niech stanie na miejscu 3–41+1–93. Ile to jest? Szybko, alchemiku. Trzydzieści jeden? No i bardzo dobrze. Firuś, kochany, pamiętaj, miejsce numer 31!

Sprawdźmy jeszcze algorytm Fiołkinii na przykładzie, który już przedyskutowaliśmy, n=13. Mamy wybrać z ciągu najmniejszą liczbę ponad 2∙13=26. Jest nią 27. Miejsce, dające rękę królewny ma zatem numer 3∙13+1–27=13. Zgadza się. Jeżeli (jak na rysunku 1) początkiem jest kółko „11”, to Firenzo staje na ostatnim, trzynastym miejscu. Ostatnim, ale przecież dającym pół królestwa, dużo kasy i rękę królewny.

***

Jest wiele uogólnień tego zadania, w tym również takie nieprzyjemne, w którym chodzi o wyrzucanie zbędnych ludzi do morza i trzeba zrobić tak, by na pokładzie zostali tylko nasi. Trochę złośliwie przeformułuję to tak. Trzeba wybrać 15-osobową sejmową komisję śledczą. Zgłoszonych jest 30 kandydatów z dwóch konkurujących partii politycznych. Aby uprościć procedurę, postanowiono ustawić wszystkich jeden za drugim (albo oczywiście tylko teczki z nazwiskami), usuwać co dziewiątą i kontynuować, aż zostanie 15. Ekspert jednej z partii doradził im, jak mają się ustawić, żeby odpadli wszyscy z tej drugiej partii, a mianowicie tak (N=nasi, O=oni):

NNNNOOOOONNONNNONOONNOOONOONNO.

Inaczej: 4–5–2–1–3–1–1–2–2–3–1–2–2–1. 

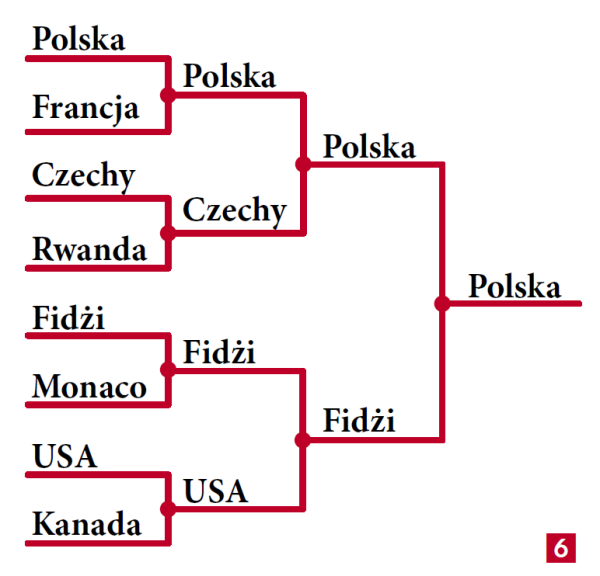
W tym ciągu liczby niebieskie oznaczają „liczba naszych”, czerwone „liczba ich”. Ale jak dojść do tego rozwiązania? A gdy kandydatów będzie mniej albo będą z trzech partii? Albo gdy będą inne reguły „losowania”? O tym może za miesiąc. 

Michał Szurek