Narzędzia matematyczne dla ucznia: GeoGebra (4)

Zacznijmy od użycia tego narzędzia jako? zwykłego kalkulatora naukowego. Powiedzmy, że chcemy wykonać następujące obliczenia:

Obliczyć wartość wyrażenia arytmetycznego 5.6 + 4.7 ? (2.4)^3.2

Niestety, musimy na oddzielenie części całkowitej i ułamkowej używać ? zgodnie z zachodnim obyczajem ? kropki, nie przecinka.

Zaczynamy od ustalenia dokładności obliczeń. W menu Opcje wybieramy ? powiedzmy ? dokładność do pięciu znaków po przecinku. Otwieramy program i po prostu wpisujemy w pole edycyjne odpowiednią formułę, po czym naciskamy Enter ? i przyjrzyjmy się, co widzimy po lewej stronie (przypominam, to okienko nazywa się widokiem algebry). Dla ustalenia naszej uwagi ilustracja pokazuje tylko górny fragment tego pola:

[caption id="attachment_4742" align="aligncenter" width="300" caption="Wynik obliczeń arytmetycznych"][/caption]

Jak widać, program nie tylko wykonał obliczenia, ale ich wynik nazwał. Ilekroć teraz w dalszych ewentualnych obliczeniach użyjemy a jako nazwy zmiennej ? program uzna, że ma ona wartość dopiero co obliczoną. Ułatwia to późniejsze przekształcenia w trybie algebraicznym.

Oczywiście, nie musimy się ograniczać do prostej arytmetyki. Mamy do dyspozycji całkiem sporo funkcji matematycznych, których wartości w punkcie danym oblicza się zupełnie tak samo. Te funkcje, to wszystkie funkcje trygonometryczne, logarytmiczne, potęgowe, hiperboliczne i wiele innych (a także ich złożenia); są one dostępne w prawym dolnym rogu okna programu. Znajdują się tam trzy pola rozwijane; pierwsze z nich to właśnie lista funkcji (oraz stałych uniwersalnych), drugie ? lista symboli alfabetu greckiego, trzecie ? lista poleceń programu. Wrócimy jeszcze do tej sprawy, bo kwestii poleceń programu warto poświęcić więcej uwagi. W tym miejscu zauważmy tylko, że wybranie odpowiedniej pozycji z którejkolwiek listy powoduje wstawienie jej do pola edycyjnego.

[caption id="attachment_4744" align="aligncenter" width="300" caption="Dostęp do list funkcji, symboli i poleceń"][/caption]

Nie będę tu pokazywał obliczania na przykład sin(2) czy tg (3), bo nie różni się ono w istocie niczym od obliczania wartości formuły, którą rozważaliśmy nieco wyżej. Po prostu, wpisujemy odpowiedni związek do pola edycyjnego ? i już (ewentualnie wybieramy sobie nazwę odpowiedniej funkcji z listy rozwijalnej).

Ciekawy efekt otrzymamy wpisując w pole edycyjne wyrażenie funkcyjne. Na przykład, wpiszmy tam coś takiego

abs(sin(x))^x

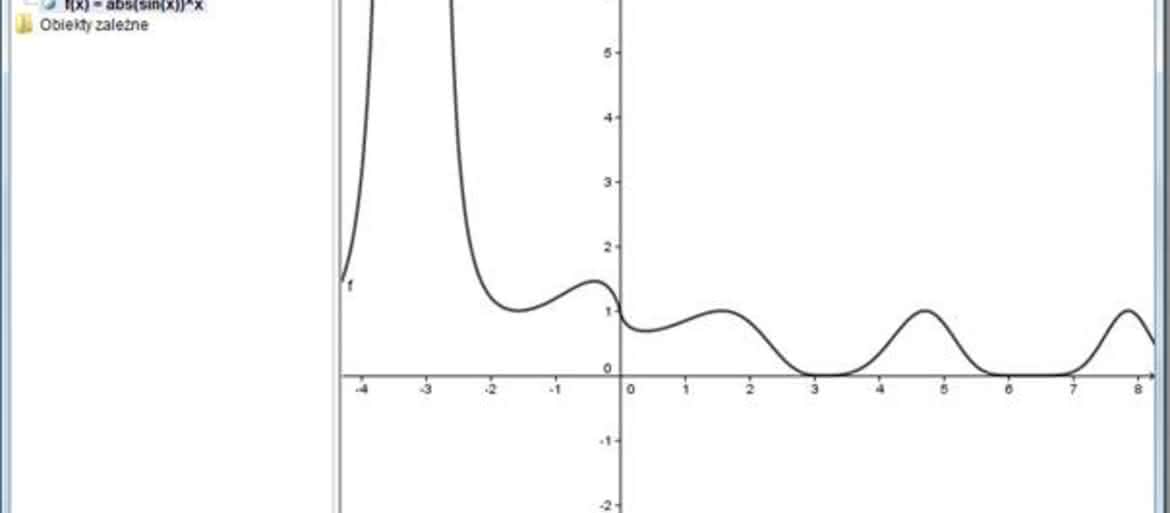
- pamiętamy, że symbol ^ oznacza potęgowanie ? i popatrzmy na wynik naciśnięcia klawisza Enter. W okienku algebraicznym mamy oczywiście zapis wprowadzonej funkcji, której program przypisał ?sam z siebie? nazwę f(x). W okienku graficznym natomiast mamy wykres tej funkcji.

Kto nie zna symbolu abs i nie rozumie sensu jego użycia: oznacza on wartość bezwzględną zmiennej w nawiasie, użyłem go zaś dla tego, ze bez tego symbolu to, co by z mojego wzoru pozostało, mogłoby nie mieć w niektórych obszarach sensu liczbowego.

 

[caption id="attachment_4748" align="aligncenter" width="300" caption="Wykres funkcji wykonany przez GeoGebrę"][/caption]

Z ciekawszych funkcji dostępnych w GeoGebrze wymieńmy ? mniej zapewne znane uczniom gimnazjów czy liceów, ale bardzo przydatne w różnego typu obliczeniach:

• Pierwiastki (stopnia, odpowiednio, drugiego i trzeciego): sqrt(x) i cbrt(x)
• Silnię !Funkcję wykładniczą exp(x) czyli w innym zapisie e^x
• Największą liczbę całkowitą mniejszą lub równą danej liczbie, czyli floor(x)
• Najmniejszą liczbę całkowita większą lub równą danej liczbie, czyli ceil(x)
• Zaokrąglenie danej liczby round(x)
• Liczbę losowa (wybieraną przez program przypadkowo) z przedziału (0, 1), oznaczaną random()

Zainteresowanym proponujemy użycie tych funkcji w różnych kombinacjach; doskonale to przybliży wam ich ciekawe właściwości.

GeoGebra zna także rachunek wektorowy. Obierzmy sobie na płaszczyźnie ? przez wskazanie w oknie graficznym ? trzy punkty A, B, i C i poprowadźmy (trzecie narzędzie od lewej) dwa wektory ? od punktu A do B i od A do C. W okienku algebry zostaną one automatycznie nazwane u i v ? i jeśli teraz w polu edycyjnym wpiszemy u+v, to w polu algebraicznym pojawi się nowy wektor w (obliczone też będą automatycznie jego współrzędne), który jednocześnie zostanie zobrazowany w okienku graficznym:

[caption id="attachment_4750" align="aligncenter" width="300" caption="Dodawanie wektorów"][/caption]

Oczywiście, możemy obliczać ? i kreślić ? nie tylko sumy czy różnice wektorów, ale ich dowolne kombinacje liniowe z dowolnymi współczynnikami. Jak również iloczyny skalarne (przypominam lub informuję nieznających tego terminu: iloczyn skalarny - to suma iloczynów współrzędnych wektorów, czyli jest to liczba; ciekawostka jest taka, ze gdy dwa wektory są prostopadłe, to ich iloczyn skalarny jest zerem); gdy w polu edycyjnym wpiszemy formułę u*v - oczywiście wartość iloczynu skalarnego pojawi się w okienku algebraicznym i zostanie jej przypisana nowa nazwa.

Również statystyka matematyczna nie jest GeoGebrze obca. Powiem więcej: program ma bardzo zaawansowane umiejętności w tej dziedzinie, znacznie przekraczające wiedzę nawet przeciętnego inżyniera. W tym miejscu więc tylko kilka zdań o sprawach absolutnie podstawowych, a często przydatnych.

Zacznijmy od wykresów statystycznych; na przykład, zajmijmy się powszechnie używanym wykresem słupkowym. Jak go wykonać za pomocą naszego programu?

Dość prosto. Wpisanie do pola edycyjnego polecenia ? powiedzmy ?

DiagramKolumnowy[0,5,2k+1,k,0,5]

I naciśnięcie ENTER da wynik taki:

[caption id="attachment_4752" align="aligncenter" width="300" caption="Wykres kolumnowy"][/caption]

 

Zajmijmy się składnią tego polecenia. Nazwa ? jak sądzę ? nie wymaga wyjaśnienie. Dalej występuje nawias kwadratowy, a w nim kolejno: pierwsza liczba (0), to początek przedziału, na którym rysujemy wykres; druga liczba (5) wyznacza koniec przedziału; funkcja zmiennej k to jest ta funkcja, której wykres słupkowy chcemy zrobić (2k+1); litera k nazywa zmienną, która występuje w poprzednim wyrażeniu (gdyby tam było 2x+1, to tu należałoby naturalnie napisać x); kolejne dwie liczby określają zakres zmienności zmiennej k. Przy okazji obliczona została jakaś liczba, nazwana przez program a; jej wartość to 30. Zastanów się skąd ona się bierze i co oznacza.

I jeszcze jeden wykres, który dobrze znają użytkownicy programu Microsoft? Excel: linia trendu, czyli regresja liniowa. Mamy pewną liczbę punktów na płaszczyźnie i chcemy zobaczyć, jak przebiega prosta, która ? spośród wszystkich dostępnych ? jest najmniej oddalona od wszystkich tych punktów jednocześnie. To bardzo ważne w różnych doświadczeniach fizycznych i biologicznych.

Popatrzmy na rysunek; w okienku algebry widzimy wyliczony związek, określający prostą trendu, w okienku graficznym ? jej wykres. Jeśli teraz skorzystamy z pierwszego narzędzia na pasku narzędziowym programu ? czyli strzałki ? i wskażemy nią dowolny z zaznaczonych punktów, to zauważymy, że możemy go przemieszczać. Gdy będziemy to robili ? zmieni się oczywiście położenie linii trendu i jej wzór. Dla eksperymentatorów ? rozwiązanie wprost idealne.

[caption id="attachment_4754" align="aligncenter" width="300" caption="Linia trendu (regresja liniowa)"][/caption]

Jak widać, GeoGebra to narzędzie rzeczywiście niezwykle potężne. Kolejne jego właściwości i możliwości ? bo to wcale nie koniec ? za miesiąc.

Cdn

(korzystałem obficie ? za zezwoleniem Autora ? ze znakomitego podręcznika GeoGebry, opracowanego przez Pawła Wimmera, który znajduje się (podręcznik, nie Paweł) tutaj.)