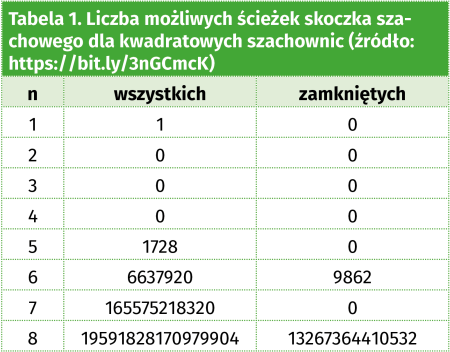
Problem skoczka szachowego

Ruch konika szachowego (1) jest następujący: dwa pola w jednym kierunku i jedno pole w bok w stosunku do pierwotnego kierunku. Ruch tej figury jest najbardziej charakterystyczną cechą łączącą szachy i inne pokrewne gry z ich przodkami, ponieważ występował już w czaturandze i nie uległ zmianie co najmniej od VII wieku n.e.
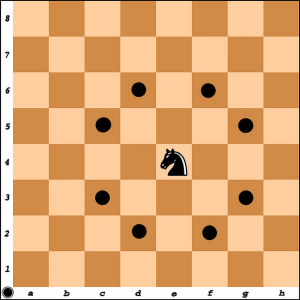
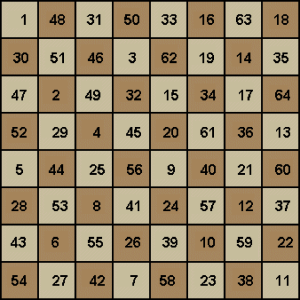
Poniżej zaznaczono osiem pól, na które może skoczyć skoczek, znajdujący się na polu e4 - jednym z centralnych pól szachownicy (2). Z rogu szachownicy konik może poruszyć się tylko na jedno z dwóch pól. Na wykresie (3) przedstawiona jest liczba możliwych posunięć, które konik może wykonać z wybranej pozycji,
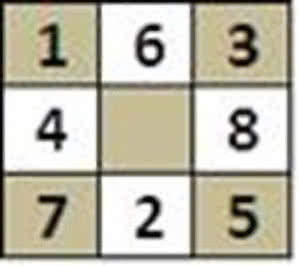
Dla planszy o wymiarach 3×3 skoczek może przemierzyć osiem pól, ale na dziewiąte, środkowe nie może wskoczyć (4). Rozpoczynając ze środka takiej planszy, skoczek nie jest w stanie wykonać poprawnego ruchu.
Nie istnieje również rozwiązanie tego problemu na planszy 4×4. Dla wszystkich plansz kwadratowych o boku większym od czterech można znaleźć taką ścieżkę otwartą dla skoczka, żeby odwiedził wszystkie pola dokładnie jeden raz. Problem skoczka szachowego na planszy n×n nazywa się też konikówką rzędu n.
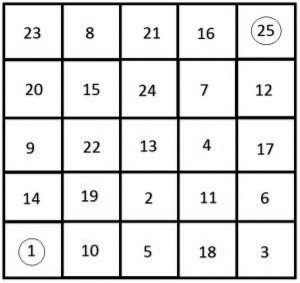
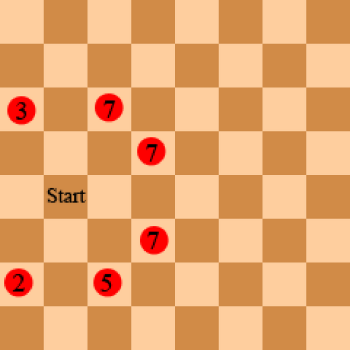
Przykład możliwej ścieżki skoczka na planszy 5×5 przedstawiony jest na rysunku 5. Na takiej planszy możliwe są tylko ścieżki otwarte, ponieważ konieczne jest wykonanie nieparzystej liczby posunięć.
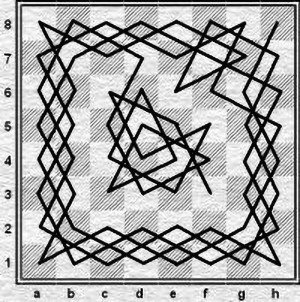
Jedno z bardzo wielu rozwiązań zamkniętej ścieżki dla szachownicy 8x8 przedstawione jest na rysunku 6. Kolejność wykonywania ruchów przez skoczka: d4 f5 d6 e8 c7 a8 b6 a4 b2 d1 f2 h1 g3 h5 g7 e6 f8 d7 b8 a6 b4 a2 c1 e2 g1 h3 f4 d3 c5 e4 c3 d5 e3 c4 e5 c6 d8 b7 a5 b3 a1 c2 e1 g2 h4 g6 h8 f7 h6 g4 h2 f1 d2 b1 a3 b5 a7 c8 e7 g8 f6 h7 g5 f3 d4.
Historia
Najwcześniejsze wzmianki o problemie skoczka szachowego pochodzą z IX wieku naszej ery. Rudrata, kaszmirski myśliciel i poeta, w sanskryckim traktacie pod nazwą Kavyalankara problem skoczka szachowego przedstawił jako skomplikowaną figurę poetycką, gdzie akcenty słów odpowiadają temu, jak przemieszcza się konik po planszy 4×8.
W 1759 roku szwajcarski matematyk Leonhard Euler (1707-1783), jeden z najwybitniejszych matematyków XVIII wieku, przedstawił pierwszą obszerną matematyczną analizę problemu skoczka szachowego na szachownicy 8×8 (7).
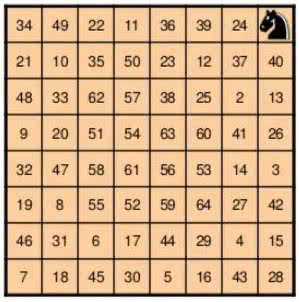
Poniżej jedno z możliwych rozwiązań (8). Kolejne ruchy numerowane są kolejnymi liczbami. Euler uzyskiwał rozwiązania, zakrywając pola, na których stanął skoczek, monetami. Zadanie to w literaturze nazywa się problemem szachowym Eulera.
Oprócz matematyki i fizyki prace Eulera dotyczyły również: teorii nawigacji, teorii muzyki, przypływów i odpływów morza, ruchów planet i komet, balistyki, dioptryki i wielu innych. Był jednym z najbardziej płodnych matematyków w historii: w sumie był autorem ok. 900 prac naukowych. Euler był wybitnym uczonym obdarzonym fenomenalną pamięcią. Pamiętał np. Eneidę Wergiliusza i mógł całą recytować słowo po słowie, pamiętając, na jakich słowach każda strona się kończy i następna zaczyna.
Po utracie wzroku przez ostatnie 11 lat życia dyktował swoje książki i rozprawy. Jedna z ostatnich rozpraw napisana pod dyktando Eulera, słynne Kompletne wprowadzenie w algebrę (Vollständige Anleitung zur Algebra) została przetłumaczona na wiele języków i stała się pierwowzorem podręcznika algebry.
Mechaniczny Turek Kempelena
Pierwszy szachowy automat, zwany Mechanicznym Turkiem, zbudował w 1769 r. Farkas Kempelen (1734-1804), znany również jako Wolfgang von Kempelen. Nie była to prawdziwa maszyna, gdyż w urządzeniu ukryty był światowej klasy szachista. Oprócz gry w szachy automat Kempelena wykonywał bezbłędnie ruchy skoczka szachowego wg zamkniętej ścieżki, rozpoczynając od dowolnie wskazanego pola.
Mechaniczny Turek (9) był to tak naprawdę pseudoautomat w postaci drewnianej figury, wielkości dorosłego człowieka. Przedstawiał postać wąsatego mężczyzny, ubranego w tradycyjny turecki strój, z turbanem na głowie, siedzącego przy biurku (skrzyni), na którym była ustawiona szachownica, wykonana z kości słoniowej. Mechaniczny Turek trzymał prawą rękę obok szachownicy, lewą zaś wykonywał posunięcia. W czasie gdy przeciwnik zastanawiał się nad swym posunięciem, Mechaniczny Turek unosił do ust fajkę, z której od czasu do czasu wydobywał się dym. Poruszał także głową i oczami.
Kempelen przed rozpoczęciem każdego występu automatu pokazywał jego wnętrze, dowodząc w ten sposób, że nie ma tam nikogo. Automat znajdował się na kółkach, niemożliwe było więc wejście do maszyny przez otwór (zapadnię) w podłodze.
Pokaz gry odbywał się z reguły w gabinecie konstruktora. Widzowie stali za balustradą - aby nie dotykać szachownicy, Kempelen podchodził do wynalazku, nakręcał tryby i rozpoczynała się gra. Zazwyczaj automat grał białymi i wykonywał pierwszy ruch. Skinieniami głowy informował przeciwnika o groźbie szacha i szacha królowej przeciwnika. Gdy przeciwnik wykonywał nielegalne posunięcie, Mechaniczny Turek wykonywał przeczący gest głową i ustawiał figurę przeciwnika na poprzednią pozycję. Automat grał agresywnie i zazwyczaj pokonywał przeciwnika w ciągu 30 minut.
Teraz już wiemy, że była to genialna mistyfikacja, a automat poruszany był przez ukrytego pod biurkiem szachistę. Był nim przeważnie jeden z graczy o najwyższej klasie mistrzowskiej, którego Kempelen na czas swych występów "wynajmował".
Tajemnica działania Mechanicznego Turka pozostała niewyjaśniona przez niemal 60 lat, chociaż takie próby podejmowali różni wynalazcy i inżynierowie. Pierwszym z nich był Joseph Racknitz, który uczestniczył w pokazie automatu w Dreźnie w 1784 roku i swoje przemyślenia przedstawił w roku 1789 w książce Über den Schachspieler des Herrn von Kempelen und dessen Nachbildung. Książka zawiera szczegółowe szkice Racknitza pokazujące interpretację, jak automat działał (10).
Kiedy Kempelen otwierał kolejno poszczególne drzwiczki ukryty szachista szybko przesuwał się w figurę Turka. Sprężyny, śruby i tryby zamontowane były tylko "na pokaz", a część elementów była wykonana z tektury. Obserwację wykonywanych posunięć na szachownicy umożliwiały ukrytemu szachiście magnesy przymocowane na nitkach pod szachownicą. Kiedy szachista podnosił figurę, magnes opadał, a kiedy stawiał ją z powrotem na szachownicy inny unosił się i "przyklejał" do deski. Szachista siedzący we wnętrzu "automatu" wykonywał swoje ruchy za pomocą pantografu poruszającego ramieniem Mechanicznego Turka. Aby ukryty szachista dobrze widział w ciemnościach skrzyni, podczas pokazu współpracownicy zapalali na biurku dwa jasne kandelabry, niezależnie od warunków oświetlenia panującego we wnętrzu pomieszczenia, w którym odbywał się pokaz.
Reguła Warnsdorffa
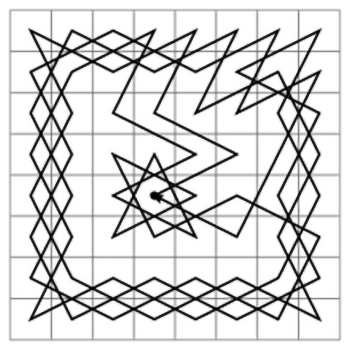
Pierwsze algorytmy (sposoby postępowania prowadzące do rozwiązania problemu) wyznaczania ścieżki konika szachowego zaprezentowane zostały przez H.C. von Warnsdorffa w książce Des Rösselsprungs einfachste und allgemeinste Lösung w 1823 roku. Zgodnie z regułą Warnsdorffa skoczek zawsze porusza się na pole, z którego ma najmniej wolnych pól (tj. jeszcze nieodwiedzonych), dostępnych na jego następny ruch (11). Ta zasada zapobiega wcześniejszemu odwiedzeniu jednego z dwóch pól, do których skoczek może dotrzeć z narożnika, aby nie mógł później uciec z narożnika. Oznacza to, że automatycznie pierwsze ruchy będą na zewnątrz i stopniowo do wewnątrz.
Zasada nie podaje żadnych instrukcji, co zrobić, jeśli jest kilka pól, z których jest kilka pól, do których można dotrzeć w następnym ruchu. Nawet jeśli istnieje rozwiązanie, zasada Warnsdorffa nie może zagwarantować, że zostanie ono znalezione, a skoczek dla dużych planszy coraz bardziej znajduje się w ślepym zaułku. Nawet na szachownicy (n=8) algorytm może zawieść, jeśli wybierze się niewłaściwą z kilku możliwych alternatyw, ale jest to bardzo mało prawdopodobne.
 12. Gerard d’Hooghe, wynalazca maszyny prezentującej trasę skoczka szachowego, źródło: https://bit.ly/31kfuZ8
12. Gerard d’Hooghe, wynalazca maszyny prezentującej trasę skoczka szachowego, źródło: https://bit.ly/31kfuZ8Program komputerowy, który znajduje trasę skoczka szachowego dla dowolnej pozycji wyjściowej, korzystając z reguły Warnsdorffa, został napisany przez Gordona Horsingtona i opublikowany w 1984 roku w książce Century/Acorn User Book of Computer Puzzles.
W latach pięćdziesiątych XX wieku farmaceuta Gerard d’Hooghe skonstruował maszynę, która demonstrowała trasę skoczka szachowego z dowolnie określonego pola wyjściowego. Jego tak zwany t’Zeepaard (zeepaard to konik morski w języku niderlandzkim) został pokazany publicznie podczas Olimpiady Szachowej w Lipsku w 1960 roku (12). Gerard d’Hooghe był honorowym prezesem klubu szachowego i autorem książki Les Secrets du Cavalier, Le Problème d’Euler, wydanej w 1962 roku, w której opisuje swój wynalazek (13).
Jest szereg strategii prowadzących do znalezienia ścieżek konika szachowego. Przykładowo na rysunkach 14a i 14b widoczne są wyraźnie dwie fazy procesu rozwiązywania problemu ścieżki konika szachowego. W pierwszej kolejności figura przemierza pola, które są najbardziej oddalone od środka szachownicy, tworząc w ten sposób pewnego rodzaju "ścianę", która pozwala skupić się na pozostałym, mniejszym obszarze do rozwiązania.
Inny przykład to strategia "sektorowa" polegająca na podziale szachownicy na sektory. Rozwiązywanie problemu tą metodą sprowadza się do odnalezienia ścieżki dla każdego z sektorów oraz spojenie ich w jedną dla całej szachownicy.
dr inż. Jan Sobótka