Systemy liczbowe
42 tys. lat p.n.e. Kość odkryta w Górach Lebombo (1) ma 29 nacięć, co, według The Universal Book of Mathematics, sugeruje, że "mogła ona być używana jako licznik faz księżycowych". Kość jest złamana na jednym końcu, więc owe widoczne nacięcia mogą stanowić jedynie część większej sekwencji obliczeniowej. Podobne artefakty, np. z Australii, również sugerują, że takie nacięcia nie muszą pełnić funkcji zapisu liczb, jednak interpretacja mówiąca o obliczaniu wydaje się naturalna i prawdopodobna.
ok. 30 tys. lat p.n.e. Przyjmuje się, iż potrzeba liczenia pojawiła się wraz z posiadaniem przedmiotów na własność, co w naturalny sposób wpłynęło na powstanie pierwszych prostych systemów liczenia. Dziś ten pierwotny system nazywamy systemem karbowym, a pojawił się polegał na żłobieniu w kościach karbów podobnie jak to miało miejsce w przypadku kości Lebombo. Jednak późniejsze artefakty nie pozostawiają już wątpliwości, że były stosowane do liczenia.
Początkowo dla wyrażenia jednostek stosowano pojedyncze kreski. Aby zwiększyć klarowność zapisu liczb, w regularnych odstępach stawiano kreskę pod innym kątem niż pozostałe. Jeśli w liczbie tak zapisanej występowało sporo takich wyróżniających się karbów, to co drugą zapisywano jeszcze inaczej. W ten sposób prawdopodobnie system karbowy wyewoluował m.in. w znany nam dzisiaj system rzymski. Rzymianie uprościli zapis karbowy odrzucając niepotrzebne kreski po lewej stronie, gdyż "znak zbiorczy" oznaczał już określoną liczbę jednostek.
4-3 tys. lat p.n.e. W okolicach czterech tysięcy lat przed naszą erą w Mezopotamii powstała pierwsza numeracja. Jej istotą było to, że jedna cyfra może oznaczać różne liczby, w zależności od miejsca/lokalizacji, w którym się znajduje w zapisie liczbowym. Jest również uważany za pierwszy znany system pozycyjny, gdzie wartość określonej cyfry zależy zarówno od niej samej oraz od jej pozycji w zapisie liczby. Stanowiło to bardzo ważny krok naprzód, ponieważ przed systemami pozycyjnymi ludzie musieli używać różnych symboli do przedstawiania potęg podstawy, a używanie specjalnych znaków dla dziesięciu, setki, tysiąca itd. powodowało, iż przeprowadzenie nawet prostych rachunków było bardzo skomplikowane.
Do zapisu zaczęto używać pisma klinowego (2). Pismo klinowe Babilończyków składało się z bardzo wielu znaków, jednak zapis liczb był dosyć prosty. W zapisie używa się dwóch znaków, oznaczających 1 i 10. System dziesiątkowy był znany mieszkańcom Międzyrzecza, ale jako najbardziej powszechni utrwalił się po 2000 roku p.n.e. system pozycyjny sześćdziesiątkowy.
Sumeryjczycy posiadali trzy różne systemy liczenia związane z ziemią, płodami rolnymi i trzodą, a dla każdego z nich stosowali całkowicie odmienne symbole do przedstawiania liczb. Chociaż babiloński system sześćdziesiątkowy może się nam wydawać dzisiaj nieporęczny, stanowił jednak wielki postęp w porównaniu z systemami liczbowymi Sumeryjczyków, żyjących przed Babilończykami. System liczbowy o podstawie 60 towarzyszy nam jeszcze dziś. Do dzisiaj dzielimy godziny na sześćdziesiąt minut, minuty na sześćdziesiąt sekund.
System babiloński może wydawać się skomplikowany, jednak w rzeczywistości Babilończycy potrzebowali tylko dwóch symboli - dla oznaczenia jedności i dziesiątek. Dużą zaletą liczby 60 jest wiele dzielników np. 2, 3, 5, 6, 12, 15, 20, 30. Babilończycy nie znali zera i najczęściej zostawiali puste miejsce, zaś w późniejszym czasie umieszczano tam pionową kreseczkę. System sześćdziesiętny nie zdominował innych kultur poza starożytnym Babilonem, ale ułamki sześćdziesiętne były używane w krajach Azji Środkowej, Europy Zachodniej, Bliskiego Wschodu i północna Afryka. Przed nadejściem ułamków dziesiętnych odgrywały ważną rolę w astronomii i innych naukach. Dziś przypomina nam o tym systemie podzielenie minuty na 60 sekund, godziny na 60 minut, kąt na 360 stopni.
W drugim tysiącleciu p.n.e. rozwinęła się dziesiętna wersja tamtejszego zapisywanego pismem klinowym systemu liczbowego, zwana dziś asyrobabilońską, odzwierciedlająca zwiększony wpływ ludów semickich, Akkadyjczyków i Eblaitów; choć dziś jest ona mniej znana z tamtych czasów niż babiloński system sześćdziesiętny, ostatecznie stała się dominującym systemem używanym w całym regionie, zwłaszcza gdy wpływy kultury sumeryjskiej zaczęły słabnąć.
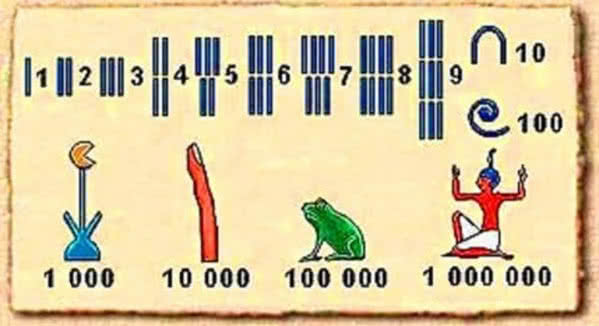
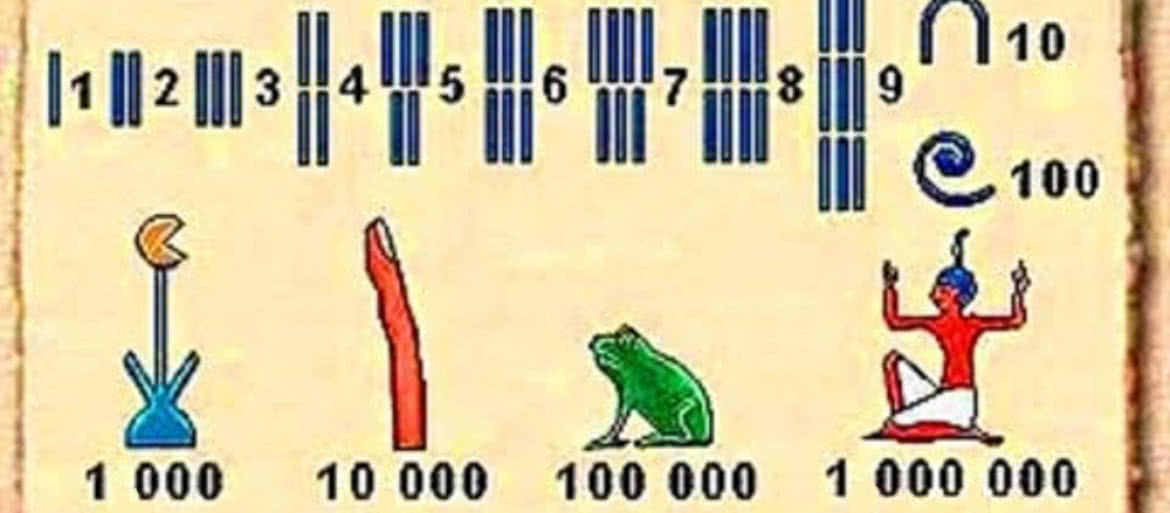
ok. 3 tys. lat p.n.e. Starożytni Egipcjanie używali systemu decymalnego (dziesiętnego). Ten system liczbowy pozwalał im na wykonywanie prostych obliczeń matematycznych, takich jak dodawanie i odejmowanie, i był szeroko stosowany w codziennym życiu i w rachunkach handlowych. W starożytnym Egipcie system ten był używany
w połączeniu z systemem sexagesimalnym (opartym na liczbie 60, podobnie jak w Babilonie) do obliczania czasów i kątów. Najprawdopodobniej był to import z Mezopotamii. W Egipcie do zapisu liczb służyły hieroglify. Każdy z symboli przedstawiał coś innego. 1 - tyczka do mierzenia, 10 - podkowa, 100 - zwinięty liść palmy, 1000 - kwiat lotosu, 10 000 - wyciągnięty palec, 100000 - żaba, 1000000 - postać z podniesionymi rękoma (3).
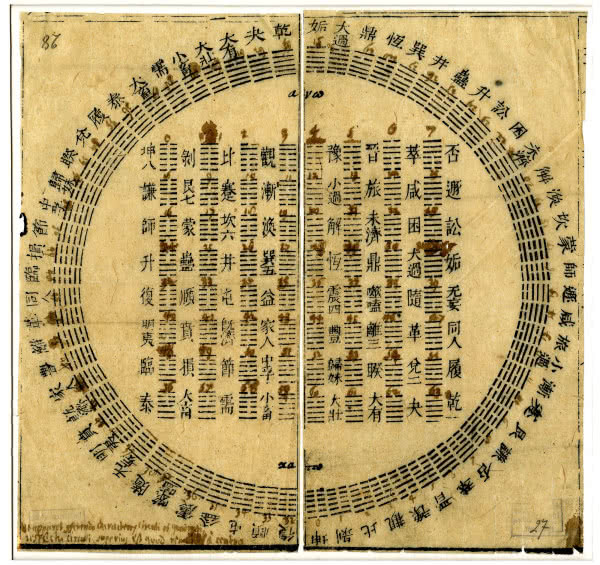
ok. 1000 p.n.e. Starożytni Chińczycy używali systemu dwójkowego (binarnego), co przyznał w swoich pismach nowożytny, europejski wynalazca tego systemu Gottfried Leibnitz, który miał okazję się zapoznać ze starymi diagramami I Ching (4). Ten system liczbowy pozwalał im na wykonywanie prostych obliczeń matematycznych, takich jak dodawanie i odejmowanie, ale nie był tak dokładny jak dziesiętny system liczbowy. Chiński system dwójkowy był używany głównie do obliczania pozycji na kostce do gry i do prognozowania pogody. W późniejszych czasach chińscy matematycy rozwijali swoje umiejętności i zaczęli stosować system dziesiętny do bardziej zaawansowanych obliczeń matematycznych.
VIII–III w. p.n.e. Liczebniki greckie oznaczane były kolejnymi literami alfabetu (5). Ich alfabet miał jednak tylko 24 litery, a potrzeba było 27, zapożyczyli więc 3 litery i użyli ich do oznaczenia liczb 6, 90 i 900. Aby zapisać liczby większe od 999 do jednej z przedziału 1–9 umieszczali w indeksie dodatkowy znak ι(jota) oznaczający pomnożenie przez 1000. Podobną funkcję miała miriada, nad którą umieszczano liczbę od 1 do 9999. Wyglądała ona w ten sposób M. Zamiast 1000 mnożyła jednak przez 10000. Starożytni Grecy używali systemu dziesiętnego (decymalnego), ale często stosowali też system sexagesimalny (oparty na liczbie 60). System sexagesimalny był szczególnie używany w astronomii i matematyce, gdzie umożliwiał dokładne obliczanie pozycji ciał nie-bieskich i kątów. W codziennym życiu system dziesiętny był powszechnie stosowany do wykonywania prostych obliczeń i do wystawiania faktur.
ok. 500 p.n.e. Starożytni Rzymianie używali systemu dziesiętnego (decymalnego). Ten system liczbowy pozwalał im na wykonywanie prostych obliczeń matematycznych i był szeroko stosowany w codziennym życiu (6) i w rachunkach handlowych. Rzymski sposób zapisywania liczb jest sposobem addytywnym, czyli wartość danej liczby określa się na podstawie sumy wartości jej znaków cyfrowych. Wyjątki od tej zasady to liczby: 4, 9, 40, 90, 400 i 900, do opisu których używa się odejmowania. Cyfry rzymskie rozwinęły się z symboli etruskich około połowy I tysiąclecia p.n.e.
W systemie etruskim symbol 1 był pojedynczym znakiem pionowym, symbol 10 był dwoma prostopadle skrzyżowanymi znakami podsumowującymi, a symbol 100 był trzema skrzyżowanymi znakami podsumowującymi (podobnymi w formie do współczesnej gwiazdki *); podczas gdy 5 (kształt odwróconej litery V) i 50 (odwrócona litera V podzielona pojedynczym pionowym znakiem) zostały być może wyprowadzone z dolnych połówek znaków dla 10 i 100, nie ma przekonującego wyjaśnienia, w jaki sposób rzymski symbol dla 100, C, został wyprowadzony ze swojego etruskiego poprzednika w kształcie gwiazdki.
200...1500 n.e. Starożytne kultury Ameryki, takie jak Majowie i Aztekowie, używały systemów liczbowych opartych na liczbie 20 lub na liczbie 5. Te systemy liczbowe były używane do wykonywania prostych obliczeń matematycznych, takich jak dodawanie i odejmowanie, oraz do oznaczania dat i mierzenia czasu. Systemy te były skomplikowane i zawierały różne symbole, takie jak kropki i kreski, które reprezentowały kolejne potęgi liczby bazowej.
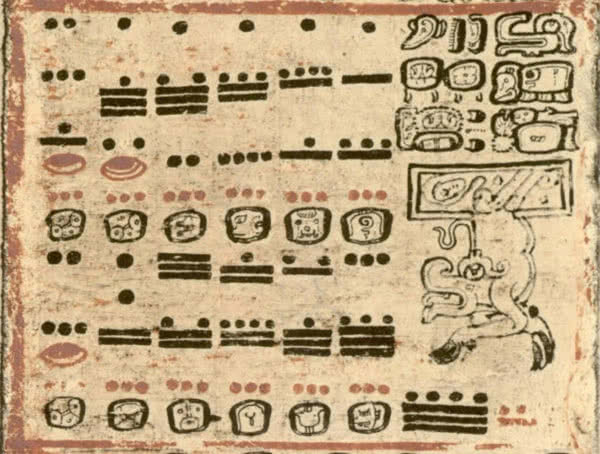
W rzeczywistości starożytne kultury Ameryki miały bardzo zaawansowane systemy liczbowe, które pozwalały im na realizację bardzo skomplikowanych projektów budowlanych, takich jak piramidy. Majowie stworzyli również własny system zapisywania liczb (7). Opierał się na trzech symbolach: kropka, kreska i muszla. Znak kropki oznaczał jednostkę, pozioma kreska oznaczała piątkę, a muszla oznaczała zero. Liczby zapisywano w postaci kombinacji kropek i kresek, odpowiednio pogrupowane stanowiły podstawowy zestaw cyfr. Ten podstawowy zestaw cyfr zbudowany został w sposób addytywny, jednak jednocześnie system Majów był systemem pozycyjnym opierającym się na podstawie dwadzieścia, choć były od niego odstępstwa.
V–XIII w. Nasz sposób zapisu liczby, którym posługujemy się na co dzień, jest znany jako system arabski lub indyjskoarabski. System dziesiętny został zapoczątkowany w Indiach i rozpowszechnił się w krajach arabskich dzięki matematykowi al-Chwarizmiemu, który w połowie VIII w. przetłumaczył na arabski indyjską książkę o matematyce. Dziewięć pierwszych cyfr oznaczających wartości od 1 do 9 były przedstawiane jako umowne znaki. Hindusi też jako pierwsi wpadli na pomysł pisania cyfr słowami. Podawali rów-nież oddzielne nazwy dla kolejnych potęg liczby 10 oraz wynaleźli zero. Do rozwoju i popularyzacji systemu dziesiętnego i zapisu zwanego arabskim w Europie przyczynił się włoski matematyk i podróżnik Leonardo Fibonacci (8). Zafascynowany systemem, w 1202 roku napisał książkę „Liber Abaci”, w której tłumaczył jak używać arabskich cyfr, jak dodawać, odejmować i wykonywać inne działania w systemie dziesiętnym.
XIII w. Ramon Llull z Majorki opracował własną metodę nazwaną "Ars generalis" opartą na binarnych kombinacjach, przez co został uznany za prekursora informatyki i sztucznej inteligencji.
1689 Binarny system liczbowy został (ponownie) odkryty przez matematyka i filozofa niemieckiego, Gotfrieda Leibnitza i opisany przez niego w traktacie pt. "Explication de l'Arithmétique Binaire" (9). Leibnitz udowodnił, że system ten może być użyty do rozwiązywania wielu matematycznych problemów. Jednak binarny system liczbowy nie był szeroko rozpowszechniony i stosowany, aż do dwudziestego wieku i rozwoju nowoczesnej elektroniki a potem komputerów, gdzie stał się podstawowym sposobem reprezentacji danych. W komputerach binarny system liczbowy był używany do reprezentowania informacji w postaci zer i jedynek, co umożliwiło komputerom wykonywanie operacji matematycznych.
Klasyfikacja systemów liczbowych
I. Systemy pozycyjne i niepozycyjne
• Pozycyjny system liczbowy
W systemach liczbowych pozycyjnych liczbę przedstawia się jako ciąg cyfr. Wartość jej jest zależna od położenia cyfry w liczbie (np. system arabski). W zależności od pozycji danej cyfry w ciągu, oznacza ona wielokrotność pewnej liczby uznawanej za bazę danego systemu. Liczby zapisujemy przy pomocy cyfr od strony lewej do prawej. W takiej konwencji zapisu, każda pozycja ma ściśle określoną i niezmienną wagę liczbową. System pozycyjny umożliwia zapisywanie ułamków, przy czym liczby wymierne składają się albo ze skończonej liczby znaków, albo są od pewnego miejsca okresowe.
Systemy pozycyjne posiadają pojedyncze symbole dla kilku pierwszych liczb. Cyfry te są kolejno umieszczane w ściśle określonych pozycjach i oznaczają mnożnik potęgi liczby n+1, gdzie n jest najwyższą liczbą reprezentowaną pojedynczą cyfrą. W momencie, gdy dana potęga nie jest potrzebna do zapisu danej liczby, zostawia się w zapisie puste miejsce lub częściej specjalny symbol oznaczający zbiór pusty. Obecnie jest to cyfra zero.
• Niepozycyjne i addytywne systemy liczbowe
Systemy niepozycyjne to metody zapisywania liczb w taki sposób, że znaczenie cyfry (wartości) jest niezależne od zajmowanej pozycji w liczbie (na przykład system rzymski). Systemy addytywne to takie, w których liczby tworzy się przez dodawanie kolejnych symboli i stąd ich nazwa (np. jeśli "X"=10, "V"=5, "I"=1 to XVI=10+5+1=16). Systemem addytywnym dziesiątkowym był system egipski, w którym uży-wano oddzielnych hieroglifów dla potęg dziesiątki aż do siódmej włącznie. Innym przykładem addytywnego systemu jest dobrze znany i wciąż stosowany rzymski system zapisywania liczb z podstawowymi wielokrotnościami 10 i 5.
II. Niektóre pozycyjne systemy liczbowe
- Dwójkowy system liczbowy lub też system binarny (NKB - naturalny kod binarny) - pozycyjny system liczbowy, którego podstawą jest liczba 2, a do zapisu liczb potrzebne są tylko dwie cyfry: 0 i 1. Znak dwójkowy (0 lub 1) nazywany jest bitem. Liczby naturalne w systemie dwójkowym zapisujemy analogicznie jak w systemie dziesiętnym - jedynie zamiast kolejnych potęg liczby dziesięć, stosujemy kolejne potęgi liczby dwa. Na n bitach można zapisać w naturalnym kodzie binarnym liczby z przedziału: 0-2n-1. Liczby zapisujemy jako ciągi cyfr (0,1), z których każda jest mnożną potęgi liczby.
- Trójkowy system liczbowy - pozycyjny system liczbowy, w którym podstawą jest liczba 3. Do zapisu liczb są potrzebne 3 cyfry: 0, 1 i 2. Cyfry trójkowe często nazywa się tritami na podobieństwo bitów w systemie binarnym.
- Siódemkowy system liczbowy to pozycyjny system liczbowy o podstawie 7. System siódemkowy jest czasem nazywany septymalnym (łac. septem - siedem). Do zapisu liczb używa się w nim siedmiu cyfr, od 0 do 6.
- Ósemkowy system liczbowy - pozycyjny system liczbowy o podstawie 8. System ósemkowy jest czasem nazywany oktalnym od słowa octal. Do zapisu liczb używa się w nim ośmiu cyfr, od 0 do 7. System oktalny.
- Szesnastkowy system liczbowy, znany również pod nazwą system heksadecymalny - pozycyjny system liczbowy, w którym podstawą jest liczba 16. Do zapisu liczb w tym systemie potrzebne jest szesnaście znaków (cyfr szesnastkowych).
- System szesnastkowy to system różny od tego, którego używamy na co dzień. Różni się o tyle, że bazuje na liczbie 16, a więc potrzebuje 16 znaków za pomocą, których można zapisać dowolną liczbę. Szesnastkowy system liczbowy jest właściwy komputerom, ponieważ pozwala na zapis większych liczb w mniejszych przestrzeniach pamięci. W systemie szesnastkowym wyróżniamy szesnaście cyfr: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Liczby zapisujemy jako ciągi cyfr, z których każda jest mnożną potęgi liczby 16.
M.U.