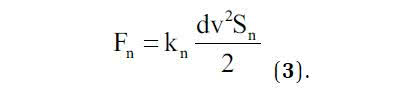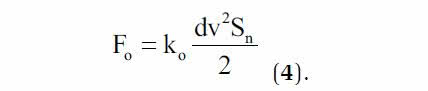Skąd samolot ma tyle siły?

Najbardziej ogólnie obiekty, które mogą swobodnie poruszać się w powietrzu, dzieli się na trzy podstawowe grupy: aerostaty, statodyny i aerodyny.
Obiekty należące do pierwszej grupy poruszają się dzięki temu, że działająca na nie siła wyporu powietrza jest większa od ich ciężaru. Średnia gęstość tych obiektów jest mniejsza niż gęstość powietrza. Przykładami takich obiektów są balony i sterowce. Mimo że zawierają one elementy konstrukcyjne o dużej gęstości, np. metalowy szkielet, to dzięki wypełnieniu pojemnych komór gazem o gęstości mniejszej niż gęstość powierza (najczęściej helem) ich średnia gęstość ulega zmniejszeniu.
Aerodyny mają średnią gęstość większą niż gęstość powietrza. Ich przykładem są samoloty i śmigłowce. Mogą utrzymywać się dzięki ruchowi powietrza, wymuszonemu względem nich przez silnik o odpowiednio dużej mocy. W przypadku samolotów istotne jest jeszcze zapewnienie tzw. powierzchni nośnej, osiągane przez dodanie skrzydeł o specjalnie wyprofilowanym przekroju.
Statodyny są przypadkiem pośrednim, dla którego siła wyporu jest tylko nieco mniejsza od ich ciężaru. "Brakującą" część tej siły uzupełnia silnik, wymuszający ruch względem powietrza, co powoduje działanie siły nośnej, podobnie jak w aerodynach. W dalszej części skoncentrujemy się na wyjaśnieniu, skąd bierze się siła nośna, utrzymująca samolot w powietrzu.
Jak zbudować przyrząd?
Bezpośrednie wykonywanie pomiarów podczas lotu prototypu samolotu w powietrzu, z prędkością setek kilometrów na dużej wysokości, byłoby trudne i niebezpieczne. Na szczęście ruch jest względny, więc zamiast wprawiać obiekt w ruch w powietrzu, można je skierować na nieruchomy obiekt.
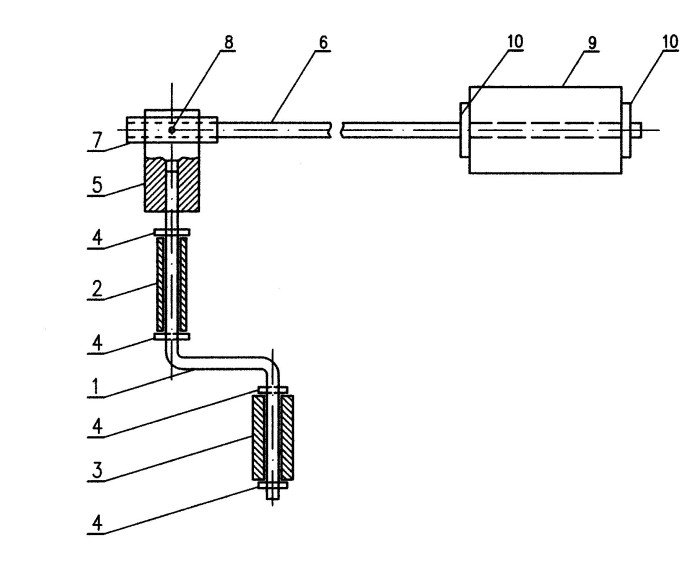
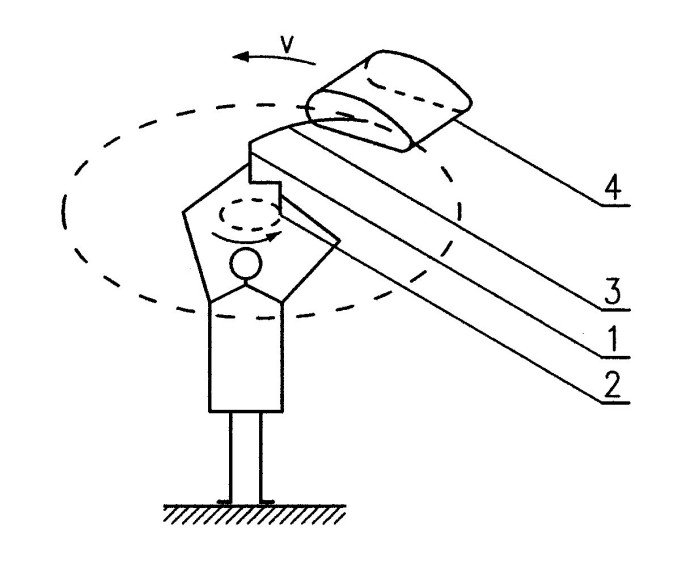
Ta idea została wykorzystana w powszechnie stosowanych tunelach aerodynamicznych. W tych urządzeniach model badanego obiektu, zaopatrzony w przyrządy pomiarowe, pozostaje nieruchomy w kanale, do którego wtłaczany jest strumień powietrza, wytwarzany przez wentylatory. Zbudowanie takiego tunelu w warunkach domowych mogłoby jednak okazać się zbyt trudne i pracochłonne. Dlatego do spowodowania ruchu badanego obiektu w powietrzu użyjemy specjalnej korbki, pokazanej na rys. 1.
Z dostatecznie sztywnego pręta - np. stalowego o średnicy ok. 4-5 mm - należy wygiąć korbkę, której każdy z odcinków będzie miał długość ok. 20-30 cm. Do tego celu bardzo użyteczny będzie dostęp do dużego imadła, np. w warsztacie ślusarskim, i ciężki młotek. Można też wykorzystać gotową korbkę o podobnych rozmiarach od jakiegoś przyrządu, albo wykonać ją przez połączenie za pomocą nakrętek dwóch kawałków nagwintowanego pręta i płaskownika z otworami wywierconymi przy jego końcach.
Na korbę należy nałożyć dwie tulejki, odcięte z metalowej rurki o średnicy ok. 0,2-0,5 mm większej niż średnica pręta. Tulejki powinny dać się swobodnie obracać na korbce. Żeby nie zsuwały się z korbki, należy zabezpieczyć je za pomocą kołeczków z drutu o średnicy 1-1,5 mm. Kołeczki wciskamy w otwory wywiercone na wylot w korbce w pobliżu końców rurek. Zamiast kołeczków można wypiłować wąskim pilnikiem, tzw. iglakiem, rowki na obwodzie korbki i wcisnąć w nie pierścienie Segera. Są to sprężyste pierścienie w kształcie litery C, z otworkami na końcach, kosztujące kilkadziesiąt groszy za sztukę. Można je kupić w sklepach z artykułami metalowymi lub motoryzacyjnym. Do zdejmowania pierścieni Segera najwygodniej używać specjalnych kleszczy z okrągłymi końcówkami.
W uproszczonej wersji przyrządu można zrezygnować z tulejki na części pokrętnej korbki.
Na górny koniec korbki wciskamy metalowy łącznik, wykonany zgodnie z rys. 2. Odpowiednim materiałem do tego celu jest kawałek aluminiowego pręta, w którym łatwo będzie wykonać wycięcie i wywiercić odpowiednie otwory.
Dla uzyskania wycięcia najpierw wykonujemy dwie równoległe szczeliny piłką do metalu, a następnie przewiercamy łącznik wzdłuż jego średnicy przy końcu szczelin i usuwamy niepotrzebny kawałek materiału. Końcowy kształt nadajemy wycięciu pilnikiem.
Średnica wykonanego łącznika wynosi 20 mm, szerokość wycięcia 8,5 mm, a jego głębokość 30 mm. Łącznik można dodatkowo zabezpieczyć przed spadnięciem z końca korbki przez posmarowanie powierzchni jego większego otworu klejem epoksydowym przed wciśnięciem, albo przewiercenie radialnie łącznika wraz korbką i wciśnięcie kołeczka z drutu.
W wycięciu łącznika umieszczony jest koniec lekkiej i sprężystej listewki o długości ok. 1 m i przekroju kwadratowym ok. 8×8 mm, połączony z nim za pomocą osi przechodzącej przez mniejsze otwory w łączniku. Bardzo dobrze nadaje się do tego listewka z balsy, którą można kupić w sklepach z artykułami dla plastyków i modelarzy w cenie kilku złotych. W pobliżu końca listewki należy wywiercić otwór do przełożenia przez niego osi, której funkcję spełnia śrubka M3 z nakrętką, przechodząca również przez łącznik. Żeby listewka nie uległa złamaniu, na jej koniec wsunięto nakładkę wzmacniającą, w postaci kilkucentymetrowego odcinka koszulki termokurczliwej, i lekko ją ogrzano w celu zaciśnięcia.
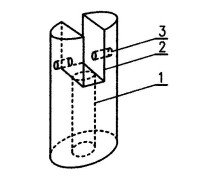
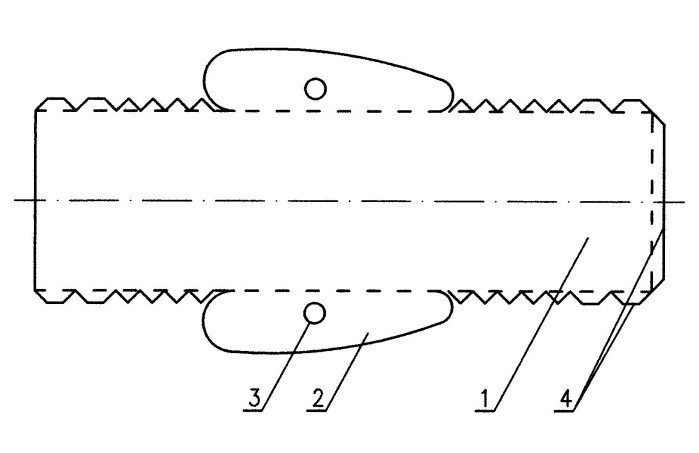
Na drugim końcu listewki będziemy umieszczali badane profile aerodynamiczne. Rozmiary tych profili powinny wynosić ok. 20-25 cm. Przykład takiego profilu w postaci fragmentu skrzydła samolotu przedstawia rys. 3. Profile muszą być lekkie, dlatego najlepiej wykonać je jako puste bryły sklejone z kartonu. Rozwinięcie profilu z rys. 3 na płaszczyznę, dające siatkę, przeznaczoną do sklejenia, pokazano na rys. 4. Do sklejenia profilu służą wypustki na brzegach, które należy zagiąć pod kątem prostym do wewnątrz i posmarować klejem. Można też zrezygnować z wypustek i do sklejenia użyć taśmy klejącej, przyłożonej wzdłuż zewnętrznych krawędzi profilu.
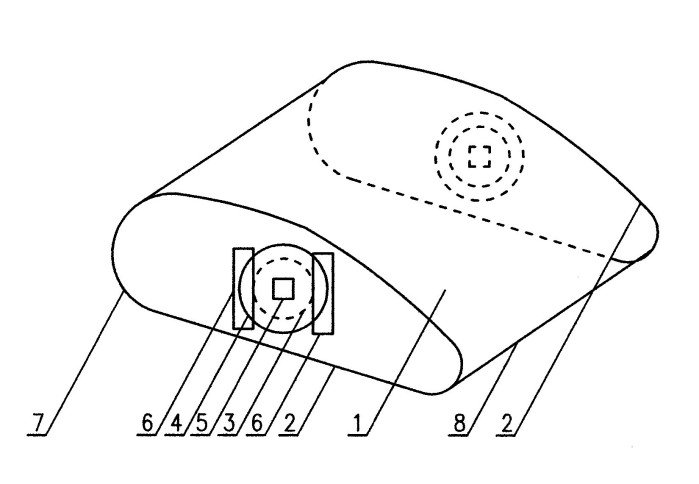
W celu łatwej wymiany profili wycinamy dwa naprzeciwległe, okrągłe otwory o średnicy ok. 20 mm w ich bocznych ściankach. Ponadto wykonujemy z tektury dwie okrągłe nakładki o średnicy ok. 25 mm, w których wycinamy kwadratowe otwory dokładnie o takich samych rozmiarach, jakie ma przekrój poprzeczny listewki, czyli 8×8 mm. Nakładki te będziemy wsuwali na listewkę wraz z umieszczonym między nimi profilem i następnie, po jego obróceniu, przyklejali do bocznych ścianek profilu taśmą klejącą (rys. 3). Umożliwia to łatwe mocowanie profili do listewki pod dowolnie wybranym kątem. Jeden z gotowych przyrządów został pokazany na fot. 1.
Doświadczenia i trochę teorii
Sposób użycia przyrządu przedstawia rys. 5. Przyrząd trzymamy mocno jedną dłonią za tulejkę umieszczoną na części chwytowej i unosimy wysoko ponad głowę. Listewka z balsy, obciążona na końcu profilem aerodynamicznym, pozostaje wtedy odchylona w dół i może ulec lekkiemu ugięciu pod ciężarem profilu i ciężarem własnym. Trzymając przyrząd nieruchomo w tej pozycji, chwytamy drugą dłonią za tulejkę na części pokrętnej korbki i zaczynamy nią obracać.
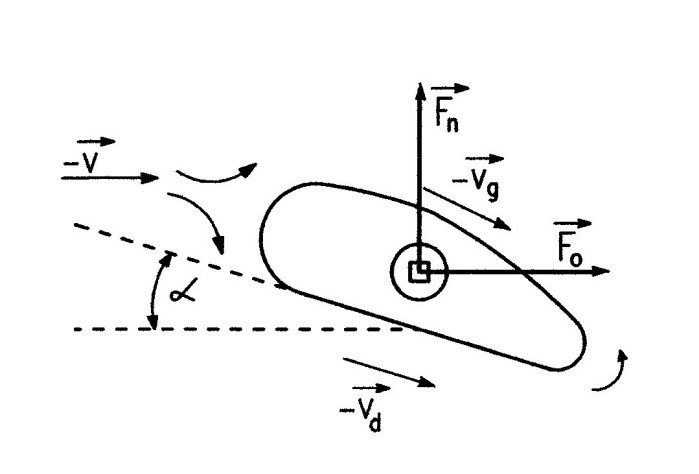
Zauważamy, że profil wraz z listewką unosi się ku górze, tym bardziej, im szybciej obracamy korbką. Ponadto listewka ulega lekkiemu wygięciu w kierunku przeciwnym do kierunku obrotu. Dlaczego tak się dzieje? Unoszenie się listewki jest spowodowane siłą nośną Fn, działającą na profil podczas jego ruchu z prędkością v względem otaczającego powietrza (rys. 6). Siła ta jest skierowana pionowo, zwrócona w górę i ma wartość większą niż ciężar profilu z listewką, stąd powoduje jego unoszenie.
α - kąt natarcia.
Wartość tej siły wzrasta wraz ze wzrostem prędkości v, więc podczas szybszego obrotu profil unosi się wyżej. Ponadto na profil działa siła oporu powietrza Fo skierowana poziomo i przeciwnie do kierunku ruchu. Ponieważ wycięcie w łączniku uniemożliwia skośne ustawienie listewki w płaszczyźnie poziomej, listewka ulega wygięciu.
Kolejne pytanie brzmi: dlaczego pojawia się siła nośna? Dokładniej wyjaśnia to rys. 6. Załóżmy, że poruszamy się wraz z profilem z prędkością v. Wtedy na profil napływa strumień powietrza z prędkością-v. Trafiający na przednią powierzchnię profilu, nazywaną powierzchnią natarcia, strumień powietrza rozdziela się na dwa strumienie, z których jeden porusza się nad profilem, a drugi pod nim. Oba strumienie spotykają się jednocześnie za profilem w pobliżu powierzchni, nazywanej powierzchnią spływu.
Ponieważ strumień opływający profil od góry ma dłuższą drogę do przebycia niż strumień opływający profil od dołu, musi on poruszać się z większą prędkością (co do wartości bezwzględnej). Pomijając siły lepkości i zawirowania powietrza, dla obu strumieni można napisać równanie Bernoulliego. Jest to podstawowe równanie mechaniki płynów doskonałych (tzn. nie lepkich, nie ściśliwych), które wynika z zasady zachowania energii. Korzystając z oznaczeń przyjętych na rys. 6, mamy wtedy:
W równaniu (1) d oznacza gęstość powietrza. Zakładamy, że jest ona stała dla obu strumieni, bo uznaliśmy powietrze za nieściśliwe. Symbole pg oraz pd oznaczają ciśnienia statyczne w obu strumieniach. Po podniesieniu prędkości do kwadratu równanie (1) przyjmuje postać:
Wynika stąd, że zwrot prędkości nie ma tutaj znaczenia. Jest więc wszystko jedno, czy poruszamy profilem względem nieruchomego powietrza, czy dmuchamy powietrzem na nieruchomy profil. Jak ustaliliśmy wcześniej |–vg| > |–vd|, wtedy dla spełnienia równania (2) musi być pg < pd. Na dolną powierzchnię profilu działa więc większe ciśnienie, które powoduje pojawienie się siły nośnej Fn zwróconej ku górze.
Wzór na wartość siły nośnej można by więc wyprowadzić z równania (2), przenosząc wyrazy, zawierające prędkości na jedną stronę, a ciśnienia na drugą, i mnożąc je przez powierzchnię profilu. Ponieważ obliczenie obu prędkości nie jest sprawą łatwą, w praktyce korzysta się ze znacznie bardziej użytecznego wzoru, w którym występuje tylko jedna prędkość napływającego powierza v. Wzór ten ma postać:
Wielkość kn we wzorze (3) nazywa się współczynnikiem siły nośnej, zaś Sn jest polem powierzchni stycznej od dołu do profilu i nazywa się powierzchnią nośną. Wartości współczynnika kn zostały wyznaczone doświadczalnie dla danego typu profili.
Ponadto zależą one od kąta a, zawartego między powierzchnią styczną od dołu do profilu i kierunkiem prędkości, nazywanego kątem natarcia, który może przyjmować zarówno wartości dodatnie, jak i ujemne.
Co ciekawe, dla pewnych wartości α, nieprzekraczających kilkunastu stopni, wartości kn najpierw rosną, a później maleją. Przykładowo: dla α=0o kn=0,6, dla α=14o kn=1,4, zaś dla α=17o kn=1,3.
Wynika stąd praktyczny wniosek, że kąt natarcia nie może być zbyt duży, czyli samolot nie może się wznosić zbyt stromo, ponieważ grozi to utratą siły nośnej. Tłumaczy to również wypadki lotnicze, spowodowane tzw. przeciągnięciem czy zbyt dużym przechyleniem drążka sterowego "na siebie". Skutkiem tego jest ustawienie w dół klap na krawędziach spływu skrzydeł i stateczników, co daje wzrost kąta natarcia.
Jak wspomniano wcześniej, na profil działa też siła oporu aerodynamicznego Fo, powodującego ugięcie listewki. Wartość tej siły oblicza się ze wzoru (4), analogicznego, jak dla siły nośnej:
Wielkość ko we wzorze (4) oznacza współczynnik oporu aerodynamicznego. Jego wartości rosną zarówno dla dodatnich, jak i ujemnych kątów natarcia α. Na szczęście, wartości ko dla tych samych kątów a są mniejsze niż wartości kn.
Przykładowo: dla α=0o ko=0,03, a dla α=14o ko=0,18. Stąd też płynie praktyczny wniosek, że wzrost kąta natarcia zwiększa siłę oporu. To z kolei może powodować zmniejszenie prędkości samolotu (moc silnika jest przecież ograniczona). W konsekwencji dochodzi do jeszcze większego zmniejszenia siły nośnej, która zgodnie ze wzorem (2) maleje wraz z kwadratem prędkości. Wtedy to samolot zamiast się wznosić, zaczyna spadać.
Jeżeli taka sytuacja zdarzy się kilka kilometrów nad powierzchnią Ziemi, gdzie jest tzw. zapas wysokości, na którym uda się odzyskać kontrolę nad maszyną, wtedy wszystko może się skończyć szczęśliwie. Na małej wysokości - np. podczas startu albo akrobacji lotniczych - może być znacznie gorzej. Wniosek końcowy jest taki, że bezpieczne pilotowanie samolotu do łatwych zadań nie należy i wymaga uwzględnienia wielu parametrów oraz dużego doświadczenia.
Korzystając ze zbudowanego przyrządu, można powtórzyć opisane doświadczenia dla innych profili, stanowiących fragment skrzydła samolotu o innym przekroju, innych rozmiarach itd. Czytelnicy zajmujący się modelarstwem na pewno nie będą mieli problemu z wykonaniem takich profili. Na końcu listewki można też umieszczać płaskie tarcze, np. w kształcie koła czy kwadratu, nachylone pod różnymi kątami do kierunku ruchu. Wtedy możemy porównywać głównie siły oporu, przejawiające się różnym ugięciem listewki w kierunku przeciwnym do kierunku ruchu. Wykorzystując wzory (3) i (4), oraz rozmiary wykonanych profili, przyjmując gęstość powietrza d podaną na tablicach fizycznych oraz wyznaczając wcześniej prędkość ruchu v, można obliczyć wartości siły nośnej Fn i siły oporu Fo. W warunkach naszego doświadczenia są to niewielkie wartości i wynoszą zwykle ok. 0,01-0,1 N.
Dwie dygresje
Ponieważ wnioski praktyczne wynikające z przeprowadzonych doświadczeń zostały już podane wcześniej, na zakończenie zrobimy dwie dygresje.
Pierwsza będzie natury historycznej. Pod koniec lat 20. ubiegłego wieku polski inżynier Edmund Romer, syn znanego polskiego geografa i kartografa Eugeniusza Romera, uruchomił we Lwowie produkcję m.in. pomocy naukowych. Wśród nich była karuzela aerodynamiczna.
Przyrząd ten zawierał zamocowany przegubowo i obracający się w płaszczyźnie poziomej pręt. Na końcu pręta były umieszczane różne profile aerodynamiczne. Przyczepiane do pręta dynamometry umożliwiały pomiar sił działających na te profile. Pręt był wprawiany w ruch za pomocą bloczka, osadzonego na pionowej osi przegubu, na który nawijało się nić przywiązaną do opadających obciążników. Przyrząd ten pozwalał na łatwe wykonywanie ilościowych doświadczeń z aerodynamiki nawet w tych szkołach, które znajdowały się w miejscowościach pozbawionych sieci elektrycznej.
Przypomnijmy tu, że elektryfikację niektórych miejscowości w Polsce prowadzono jeszcze pod koniec lat 60. XX w. Okazało się, że opisany w tym artykule "przyrząd korbkowy" przypadkiem nawiązuje do karuzeli aerodynamicznej z ubiegłego wieku. Inżynier Edmund Romer po II wojnie światowej pracował na Politechnice Śląskiej i stał się znany jako wybitny konstruktor przyrządów pomiarowych. Otrzymał za to m.in. doktorat honorowy tej uczelni.
Przedstawione w tym artykule wyjaśnienie, skąd bierze się siła nośna, jest z konieczności uproszczone, choćby ze względu na ograniczoną objętość tekstu. Nie uwzględnia ono m.in. roli wirów, które tworzą się przy powierzchni spływu i na brzegach profilu, lepkości powietrza, zmian jego gęstości itd.
Podany ogólny podział obiektów latających nie uwzględnia m.in. ornitopterów czy entomopterów. Pierwsze z nich to konstrukcje z ruchomymi skrzydłami, naśladujące lot ptaków. Do drugich zaliczane są te, które naśladują lot owadów, bardzo szybko poruszających skrzydłami, np. much lub trzmieli.
Właśnie trzmiel stał się tematem pewnego żartu, powtarzanego przez wiele lat wśród specjalistów od aerodynamiki i lotnictwa. Jeżeli przeprowadzić dokładne obliczenia siły nośnej dla tego owada, stosując równanie Bernoulliego, czy nawet równanie Naviera-Stokesa (uwzględniające lepkość powietrza), wprowadzić do tych obliczeń masę trzmiela, powierzchnię jego skrzydeł, częstotliwość poruszania nimi oraz wszystkie inne dostępne parametry, to okazuje się, że wartość siły nośnej jest dziesięć razy mniejsza niż ciężar trzmiela. Stąd prosty wniosek, że trzmiele… nie mogą latać. Na szczęście one nie znają równań aerodynamiki i od dziesiątków tysięcy lat latają sobie spokojnie.
Obecnie już wiadomo, że owady podczas bardzo szybkiego poruszania skrzydłami powodują wiry powietrza, w których dochodzi do dużych zmian ciśnienia. W ich przypadku właśnie to jest główną przyczyną wytwarzania siły nośnej. Chodzi więc o zupełnie inny sposób niż w przypadku skrzydła samolotu, gdzie wiry są czynnikiem ubocznym - czy wręcz szkodliwym, bo zwiększają siłę oporu i zużycie paliwa.
Okazało się przy tym, że ogólne prawa fizyki pozostają nadal słuszne, tylko należało je umiejętnie zastosować. Co więcej, ten sposób wytwarzania siły nośnej przez owady jest bardziej efektywny, ponieważ wymaga dostarczenia znacznie mniej energii na jednostkę masy obiektu latającego.
To właśnie tłumaczy, dlaczego tak ciężki trzmiel, wyposażony w skrzydła o stosunkowo małej powierzchni, lata sobie w najlepsze. Nic więc dziwnego, że wyjaśnienie tajemnic lotu owadów stało się ostatnio przedmiotem intensywnych badań. Czy zastosowanie wyników tych badań zapewni oszczędność paliwa i tańsze bilety lotnicze - tego jeszcze nie wiadomo.
Zobacz także:
Bezpilotowe samoloty pasażerskie
Zabawki wojny
Solarny samolot
Stanisław Bednarek