Microsoft Mathematics - świetne narzędzie dla ucznia (1)

Firma Billa Gatesa (wprawdzie on sam już jest ?osoba prywatną?, ale jest w końcu jej nieusuwalna ?twarzą?) umieściła ostatnio w Internecie znakomite narzędzie z rodzaju, zwanego przez informatyków CAS (Computer Algebra System ? system algebry komputerowej). Istnieją wprawdzie narzędzia o znacznie potężniejszych możliwościach, ale to wydaje się szczególnie dobrze dostosowane do potrzeb ucznia ? a nawet studenta uczelni technicznej. MM potrafi rozwiązywać dowolne równania, robić wykresy funkcji jednej lub dwóch zmiennych, różniczkować i całkować oraz ma wiele innych umiejętności, o których później.

Wykonuje obliczenia zarówno numerycznie (na liczbach rzeczywistych i zespolonych), jak i symbolicznie, przekształcając odpowiednio formuły. Ważne jest to, że nie ogranicza się przy tym do podania ostatecznego wyniku, ale przedstawia obliczenia pośrednie wraz z uzasadnieniami; oznacza to, że jest on idealny do rozwiązywania wszelkiego typu prac domowych. Jedyne ograniczenia polega na tym, że trzeba znać angielski. No, ale ?matematyczny? angielski to raptem kilkaset słówek?

Program nazywa się Microsoft Mathematics, poprzednio kosztował ok. 20 USD, od wersji czwartej jest całkowicie bezpłatny. Jest do pobrania tutaj. Zanim to jednak zrobicie, sprawdźcie, czy wasz komputer spełnia wymagane warunki; a są one takie: system operacyjny co najmniej Windows XP z SP3 (oczywiście może być Vista albo Windows 7), zainstalowany Microsoft .NET Framework 3.5 SP1, procesor z zegarem 500 Mhz (minimum) lub 1 GHz (zalecany), RAM minimum 256 MB (zalecane 500 MB lub więcej), karta graficzna z minimum 64 MB własnej pamięci, minimum 65 MB wolnego miejsca na dysku.

Nie są to specjalnie duże wymagania, więc po ściągnięciu pliku instalacyjnego z podanego adresu przystępujemy do banalnej instalacji i uruchamiamy program.

Pojawia się takie oto okno robocze:

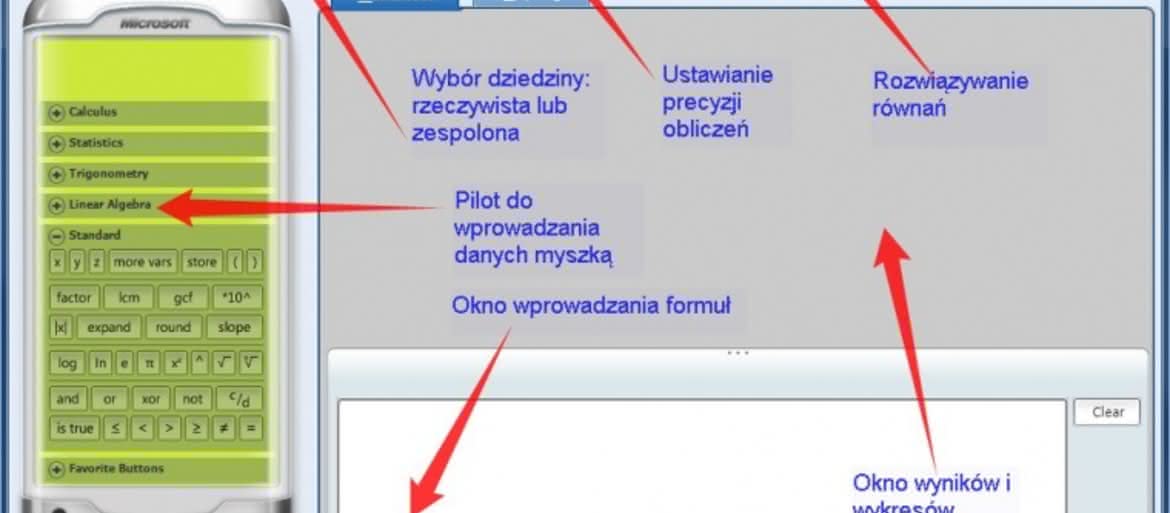
Najważniejsze jest po prawej stronie: to takie dwa okna, które po otwarciu programu będą puste. Na samym dole (białe, wąskie, z literą ?i?) jest okienko informacyjne, właściwie zbędne, choć w toku obliczeń pojawiają się w nim wyjaśnienia i podpowiedzi; drugie ? to okno wprowadzania formuł, możemy to robić zarówno z klawiatury, jak i korzystając z widocznego po lewej stronie ?pilota? z przyciskami; w wypadku wybrania tego drugiego narzędzia do obsługi programu wystarczy w zasadzie myszka. Wynik obliczeń ? to znaczy przekształcone formuły lub odpowiedni wykres ? pojawiają się w drugim okienku strefy roboczej, tym początkowo szarym, zatytułowanym ?Worksheet?; warto zauważyć, że obok zakładki z tym właśnie napisem jest zakładka ?Graphing?, której użyjemy ? jak się łatwo domyśleć ? gdy będziemy chcieli badać wykresy funkcji.

Badając wstępnie interfejs programu warto zwrócić jeszcze uwagę na trzy pola, wskazane na załączonym obrazku strzałkami. To przycisk wyboru dziedziny obliczeń (?Real? czyli liczby rzeczywiste lub ?Complex? czyli liczby zespolone) ; okienko ?Decimal Places?, czyli ustawienia precyzji obliczeń (liczby cyfr po przecinku; najlepiej zostawić ?Not fixed? ? wtedy komputer sam sobie dobierze dokładność); wreszcie przycisk ?Equation Solver?, którego wciśnięcie powoduje, że komputer będzie analizował wprowadzone formuły i ewentualnie rozwiązywał równania. Pozostałe przyciski warto pozostawić na razie bez zmian (jeden z nich, z napisem ?Ink? jest użyteczny wyłącznie dla urządzeń z ekranem dotykowym).

Pora na dokonanie pierwszych obliczeń.

Rozwiążmy równanie kwadratowe

x²-4=0

Sposób 1 wprowadzania zadania: ustawiamy kursor w oknie wprowadzania formuł i naciskamy kolejno klawisze x, ^, -, 4, =, 0. Zauważmy, że użycie znaku ^ spowoduje uzycie jako znaku potęgowania strzałki skierowanej ku górze.

Sposób 2 wprowadzania zadania: na ?pilocie? po lewej stronie klikamy myszką zmienną x, znak potęgowania ^ i odpowiednie dalsze klawisze.

W obu wypadkach w okienku wstawiania formuł pojawi się oczywiście nasze równanie. Klikamy teraz na klawiszu ?Enter? po prawej stronie okienka wprowadzania ? i w okienku wynikowym pojawia się na samej górze zapis zadania w języku programu:

solvex²-4=0,x

co oznacza ?rozwiąż równanie w nawiasie względem x), poniżej zaś trzy wiersze z niebieskimi plusikami, opisane ?solution steps?. Oznacza to, że program znalazł aż trzy sposoby rozwiązywania zadania i zostawia nam wybór, który chcemy ujawnić (możemy obejrzeć oczywiście wszystkie). Poniżej program podaje wyliczone dwa pierwiastki.

Dla przykładu rozwińmy drugi sposób rozwiązywania. Oto, co zobaczymy na ekranie:

Jak widać, program pokazuje, że dodał do obu stron równania 4, następnie wyciągnął pierwiastek kwadratowy, wziął go z plusem i minusem ? i wypisał rozwiązania. Wystarczy przepisać wszystko do zeszytu ? i praca domowa odrobiona.

Powiedzmy teraz, że chcemy mieć wykres funkcji

y= x²-4

Postępujemy tak: przestawiamy widok ekranu na ?Graphing?. Pojawia się okno wprowadzania równania; możemy wprowadzić po kolei kilka równań, żeby zobaczyć ich wzajemne relacje. Z początku pokazane są pola tylko do wprowadzenia dwóch, ale wprowadzimy tylko jedno, w pole zacienione. Możemy skorzystać z klawiatury, albo ? jak poprzednio ? z pilota. Następnie wciskamy przycisk ?Graph? ? i pojawia się wykres taki jak na załączonym zrzucie.

Warto zwrócić uwagę, że po wyborze okna graficznego zmieni się wstążka menu i będziemy mieli możliwość dokonania różnych formatowań wykresu. Możemy więc go przybliżyć lub oddalić, ukryć osie, ukryć zewnętrzna ramkę, ukryć siatkę. Możemy także ustalić zakres pokazywanej zmienności parametrów i zachować uzyskany wykres jako obraz w kilku najpopularniejszych formatach graficznych. Na samym dole okienka ?Equations & Functions? jest jeszcze interesująca możliwość wyświetlenia kontrolek animacji wykresu ?Graph controls?; efekt ich użycia radze sprawdzić samemu.

Inne funkcje programu ? następnym razem.