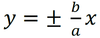Zadania matematyczne w życiu codziennym. Myśli na rok 11111100000
W początkach listopada 2015 r. uczestniczyłem w spotkaniu nauczycieli matematyki z całej Polski. Tradycyjne to spotkanie przygotowała jedna z niewielu organizacji, troszczących się o kształcenie nauczycieli matematyki w naszym kraju, a mianowicie SEM, czyli Stowarzyszenie na rzecz Edukacji Matematycznej. Artykuł do mojego kącika matematycznego, który miał stanowić pewien raport dotyczący tego spotkania, był już prawie napisany, gdy zdarzyło się to, o czym niżej. Był czwartkowy wieczór, około siódmej wieczorem. Wracałem autobusem linii 190 do domu. Usiadłem obok wysokiej, ładnej licealistki. Rozmawiała przez telefon z koleżanką. Trafiłem na koniec rozmowy:
- ... miałaś rację, ten biustonosz, co mi go polecałaś, jest bardzo dobry, wybrałam się w nim na bieganie, a przebiegłam 45 minut, no i wiesz co, mam takie dwa zadania z matematyki, to mi powiesz, czy dobrze robię, pierwsze to takie, ile to jest jedna druga z jednej ósmej, to ja to umiem, bo to tak, jak na chemii, to jest proporcja na x, jedna ósma to sto procent, a ta niewiadoma to x, to łatwa proporcja, wychodzi jedna szesnasta, a to świetnie, że dobrze zrobiłam, ale teraz jest drugie zadanie, mam cenę 28 zł za metr, to ile metrów mogę kupić za 336 zł, i tu mi nie wychodzi, nie mogę zrozumieć, gdzie mam to x postawić, a w ogóle to na co to jest proporcja... przepraszam cię, bo siedzący koło mnie starszy pan chyba zasłabł, proszę pana, proszę pana, czy pan się dobrze czuje, może lekarza...?
(autentyczne jest tu wszystko, z danymi liczbowymi włącznie, choć przyznam, że o lekarzu dodałem dla udramatyzowania sytuacji...).
Chciałem naprawdę się wtrącić, ale licealistka już zbierała się do wyjścia. A ja zamyśliłem się. Dziewczyna potrzebuje równań na wyliczenie połówki jednej ósmej i do obliczeń, które każdy człowiek, bez żadnego wykształcenia, umie zrobić - wystarczy chwilę pomyśleć: dwadzieścia osiem zł za metr, a mam w kieszeni 336 zł. Mogę nie umieć podzielić, ale wiem, że właśnie trzeba podzielić. Co podzielić? No, nie oceniam Was tak nisko, drodzy Czytelnicy, żeby to tłumaczyć.
Ale przy domowej kolacji zapytałem o to córkę, która ma wyższe wykształcenie muzyczne, ile to jest: jedna druga jednej ósmej? Odpowiedziała: "tato, dla każdego muzyka jest to oczywiste, że nuta dwa razy krótsza od ósemki to szesnastka". Zwróciłem się do drugiej córki, polonistki. Odpowiedziała: "ostatnio robiłam ciasto dla ośmiu osób, a przyszło szesnaście. Musiałam dać dwa razy mniejsze kawałki. A zatem jedna druga jednej ósmej to jedna szesnasta. Czy to cię zadowala?" Odpowiedziałem, że tak.
I z tego widać, o co chodzi. Dziewczyna z autobusu, jak wielu innych uczniów, nie widzi związku między sytuacją "życiową" a zadaniem matematycznym. Gdyby miała dzielić na połówki kawałki pizzy, pokrojonej na osiem części, nawet nie przyszłoby jej do głowy, że rozwiązuje to samo zadanie matematyczne, na połówkę jednej ósmej. Ale ona widzi Matematykę przez duże M i być może srogiego pana albo srogą panią, która wymaga, by robić wg algorytmu: zawsze ułóż proporcję. Spróbowałem... Jedna druga ma się tak do stu procent jak x do jednej ósmej... To ile jest równe x? Aha, 100 procent razy jedna szesnasta, czyli 6,25%? Nonsens. Aha, już wiem. 100% to jeden... zatem wynik, którego szukam, to jedna szesnasta. Rety, jaka ta matematyka jest trudna!!! Tak pewnie myślą tysiące uczniów, uczonych "poprawnie" przez "znających się na rzeczy" nauczycieli.
To nie koniec historyjki. Po kolacji opisałem sytuację koleżankom-nauczycielkom i kolegom-nauczycielom. Jeden z kolegów, dobry matematyk, działający w olimpiadach matematycznych, znany nauczyciel, odpisał, że ważniejsze jest nauczenie algorytmów bez zrozumienia. Zrozumienie przyjdzie później. Niech oblicza połówkę jednej ósmej za pomocą proporcji z iksem...
I dopiero to wprawiło mnie w obłęd. Zacząłem poszukiwać lekarza-psychiatry. Dla siebie.
Straszące ułamki
Jak to jest z tymi ułamkami? Odstraszają nawet swoim wyglądem, trudnością zapisu i działań. W sklepie nie kupujemy jednej siódmej kilograma szynki, tylko piętnaście deko. Ale znajomy góral pokazywał mi dokument, wedle którego jego prapradziadek miał siedemnaście osiemset czterdziestych części Hali Gąsienicowej. Ułamki zwykle są wypierane przez ułamki dziesiętne - podobno już na półlitrową flaszkę mówi się "pięćsetka". Umiejętność działań na ułamkach bywała wyznacznikiem znajomości matematyki - w średniowieczu na uniwersytecie, w XX wieku - w szkole podstawowej. Nie ukrywam, że obawiam się, iż w XXI wieku znów będą nauczane na uniwersytetach - dla wielu licealistów to za trudne. Przyjrzyjmy się ułamkom (zwykłym i dziesiętnym) od strony dydaktycznej.
Obecnie wprowadzamy ułamki dziesiętne po ułamkach zwykłych i mówimy, że jest to taki sam ułamek, tylko inaczej zapisywany. Wydaje się, że to naturalna droga, zgodna z historycznym rozwojem pojęcia ułamka. Warto odnotować, że w historii nauczania matematyki pojawił się i był realizowany (w szkołach radzieckich, w latach 20. ubiegłego wieku) pomysł, żeby z ułamków zwykłych w ogóle zrezygnować! Na poparcie tego poglądu przytaczano następujące argumenty. Po pierwsze, ułamki dziesiętne pod nazwą liczb dziesiętnych stanowią naturalne i najprostsze przedłużenie numeracji "w prawo". Po drugie, działania na ułamkach dziesiętnych są łatwiejsze niż odpowiednie działania na ułamkach zwykłych, gdyż są analogiczne do działań na liczbach całkowitych. Po trzecie, w ćwiczeniach na ułamki dziesiętne można się nie krępować wielkością mianownika. I wreszcie ułamki dziesiętne mają daleko większe znaczenie praktyczne i zastosowanie niż ułamki zwykłe, ponieważ są organicznie związane z metrycznym układem miar i otrzymywaniem wartości przybliżonych w dzieleniu liczb całkowitych.
Tymczasem okazało się, że... bez ułamków zwykłych to "jakoś nie idzie" i w 1931 r. stosowna uchwała Partii "ostro potępiła niedorzeczne odchylenia" i ułamki zwykłe wróciły do łask. Rzeczywiście, po opanowaniu ułamków dziesiętnych można o ułamkach zwykłych niemal zapomnieć - zwłaszcza w czasach, gdy każdy może mieć kalkulator. Ale ułamków dziesiętnych nie da się zrozumieć bez opanowania ułamków zwykłych. Ponadto:
- Ułamek 7/9 nie różni się pojęciowo od 7/10.
- Bez wprowadzenia ogólnych działań na ułamkach prawidła dodawania i odejmowania ułamków dziesiętnych byłyby trudne do wytłumaczenia, a mnożenia i dzielenia - bardzo trudne. Natomiast po opanowaniu przez uczniów działań na ułamkach zwykłych działania na ułamkach dziesiętnych stają się naturalne.
- Ułamki dziesiętne są mało przydatne w rachunku pamięciowym, a także rzadziej występują w codziennym życiu dziecka. "Pięć dziesiątych ciastka" jest czymś sztucznym, a "pół ciastka" - naturalnym. Dodanie ½ + ¾ jest pojęciowo prostsze niż 0,5 + 0,75.
- Nie należy bez uzasadnionej przyczyny odstępować od historycznej drogi rozwoju pojęć matematycznych.
- Przyczyna i skutek zmieniają role: dziesiątkowy układ miar jest następstwem wprowadzenia ułamków dziesiętnych, a nie na odwrót. Przed Rewolucją Francuską nie było w zasadzie miar opartych na podziale na dziesięć części.
Szkolne wyzwania i cnoty
Zostawmy na chwilę matematykę i pomówmy o szkole, bo jest ku temu powód. Środowisko nauczycielskie z niepokojem czeka na kolejne reformy. Wiele lat temu pisałem w swojej książce o nauczaniu, że każda nowa ekipa władzy (od 1918 r. począwszy!) zaczyna od obietnic, iż "teraz nauczycielom będzie lepiej, a szkoły nareszcie będą uczyć dobrze" - nie mam tu miejsca na rozwinięcie tematu. No i proszę, potwierdziło się po raz kolejny, nowy rząd zapowiada to samo. Oczywiście powtórzy się: "chcieliśmy dobrze, a wyszło, jak zwykle." Nie mam żadnych wątpliwości. To jest ponadczasowe. Ale uciekajmy od polityki.
Jeśli chodzi o ogólne zasady nauczania, to jest tylko jedna, a mianowicie: "Nie ma żadnych zasad". Otóż na swoich wykładach o dydaktyce matematyki na Uniwersytecie Jagiellońskim wywoływałem dyskusję na temat postawy "profesora Bielajewa", który ponad sto lat temu, za czasów carskich, uczył w liceum warszawskim - wtedy im. Chrzanowskiego, dzisiaj: Zamojskiego. Jednym z jego uczniów był Tadeusz Kotarbiński (1886-1981), późniejszy znany filozof, wieloletni prezes Polskiej Akademii Nauk. Próbował, jak mógł, przeciwstawiać się upolitycznieniu Akademii. Pytałem studentów: "czy chcesz naśladować profesora Bielajewa, którego Kotarbiński tak wysoko ocenia?
Czy zgadzasz się z kultem absolutnej poprawności jako cnoty szkolnej? Przemyśl zdanie o konieczności zachowania równowagi między wpajaniem automatyzmów i rozbudzaniem umysłów".
Pytania te nawiązywały do wspomnień Kotarbińskiego, z których przytaczam urywek.
Jak uczyli najlepsi z naszych nauczycieli? Co z ich pouczeń warto zarejestrować w katalogu zaleceń dobrej roboty nauczycielskiej? Staje mi przed oczami postać profesora Bielajewa, specjalisty od algebry szkolnej. Cóż to był za pedant! Każdy wywód algebraiczny, każde przekształcenie wzoru, każda operacja rozwiązywania układu równań musiały być dokonane wedle ustalonej kolejności kroków, bez żadnych opuszczeń ani przeskoków i wszystko musiało być zapisane w sposób całkowicie jednoznaczny. Co widzę w pedantyzmach szkolnego algebraisty? Widzę coś bezcennego: kult absolutnej poprawności jako cnoty szkolnej. Opanowawszy technikę danej umiejętności, można sobie potem dowoli dawać różne luzy w procedurze, ale trzeba przedtem przejść przez szkołę poprawności zupełnej. Nauczając, trzeba umieć pogodzić troskę o wyrabianie automatyzmów z zadaniem rozbudzania umysłów, a to jest synteza niezmiernie trudna.
Tyle Kotarbiński i tyle na temat przygody w autobusie... Nie, jeszcze jedno. Chyba każdy podpisze się pod frazesem: "szkoła ma uczyć myślenia". To prawda, ale jak zwykle, diabeł siedzi w szczegółach. Myślenie musi być oparte na wiedzy, faktach i właśnie na wyuczonych automatyzmach. Wywołuję zawsze spontaniczny sprzeciw, gdy twierdzę, że dobry kierowca to nie taki, który myśli na skrzyżowaniu. Nie, dobry kierowca już nie musi myśleć - on wie! A myślenie włącza mu się samo dopiero w nietypowej sytuacji (karetka, pijany przechodzień, możliwość oblodzenia itp.). W którym momencie nauczania trzeba już "odpuścić" ów kult bezwzględnej poprawności? Jest to być może głównym problemem całej dydaktyki. Problemem nigdy nierozwiązanym.
1906: liczby zespolone
Jednym z ciekawszych wykładów na konferencji, o której wspomniałem na samym początku, był referat koleżanki z Krakowa o zadaniach maturalnych wybitnych Polaków - chodziło o późniejszych znanych matematyków krakowskich (a właściwie galicyjskich).
Jak wspomniała koleżanka, historię ziem polskich XIX wieku omawia się najczęściej z punktu widzenia Polaków z zaboru rosyjskiego, gdzie rusyfikacja była dość ostra; dopiero w 1905 r. wywalczono nauczanie po polsku. W zaborze pruskim pod tym względem było jeszcze gorzej. Tymczasem w Galicji od 1867 r. mamy do czynienia z prawdziwą autonomią narodową - historycy często są zdania, że następne pokolenie Polaków w monarchii austro-węgierskiej nie widziałoby już sensu w walce o niepodległość; stalibyśmy się takimi Szkotami w Imperium Brytyjskim.
Autonomia narodowa polegała przede wszystkim na wprowadzeniu języka polskiego do urzędów, szkół i władz lokalnych. Chłopi w Galicji i w zaborze pruskim umieli czytać i pisać. Szkolnictwo średnie nie było aż tak elitarne, jak w zaborze rosyjskim.
Co nas tu najbardziej interesuje - zadania na egzaminy maturalne układały sobie same szkoły. Dopuszczalne i praktykowane było dobieranie zadań indywidualnie dla pojedynczych uczniów. Ogólnie rzecz biorąc, lepszy uczeń dostawał... trudniejsze zadania. Dziwne, ale tak było. I oto już konkrety. W jednej ze szkół krakowskich, w 1906 r., dano na maturze takie oto zadanie:
Rozwiązać równanie x³ = 8.
No, to jakie jest rozwiązanie? Proste: x = 2?
Tak, dzisiaj, w XXI wieku. Sto lat temu było inaczej... Jak to możliwe, czyżby dwa razy dwa razy dwa nie równało się wtedy osiem?
Otóż uczniowie gimnazjów galicyjskich znali liczby zespolone. Jeszcze niedawno mówiono o nich w niektórych szkołach. Dzisiaj trzy czwarte moich studentów na uczelni typu politechnicznego nie potrafi nimi się posłużyć. Wprowadzę te liczby "metodą historyczną".
Przypatrzmy się najpierw, jak Girolamo Cardano ok. 1539 r. pokonywał trudności myślowe związane z - jak się wkrótce to nazywało - wielkościami urojonymi.
Zadanie. Podzielić 10 na dwie części, których iloczyn jest równy 40.
Cardano pisze mniej więcej tak:
To oczywiście niemożliwe. Jednakże zróbmy, co następuje: podzielmy 10 na dwie równe części, każda równa 5. Mnożymy je - dostaliśmy 25. Odejmij 40 od otrzymanego 25. Pozostaje -15. Teraz widzimy, że wielkość √15 dodana i odjęta od 5 daje liczby, których iloczyn wynosi 40. Te liczby to 5 - √15 oraz 5 + √15.
Sprawdzenie wyniku przeprowadza Cardano wg dzisiejszych standardów:
Nie zważając na tortury umysłu, jakie się z tym wiążą, pomnóżmy 5 + √15 przez 5 - √15. Otrzymujemy 25 - (-15) , co jest 25 + 15. Zatem iloczyn jest 40.... To jest prawdziwie wyrafinowane.
A zatem wielkości √-15 nie ma..., a jednak jest. Podobnie musieli postępować uczniowie w XIX i XX wieku w Galicji. Do rozwiązania równania trzeciego stopnia rozkładali lewą stronę na czynniki:
x³ - 8 = (x-2)(x+1+√-3)(x+1-√-3)
i otrzymywali trzy pierwiastki równania:
x=2 x=1+√-3 x=1-√-3
Tak, tak, pierwiastek z minus trzech. Słucham? Nie ma liczby, która podniesiona do kwadratu jest ujemna? A właśnie, że jest... np. √-3 . Nie, Czytelniku, nie kpię sobie. Ale tak właśnie przez kilkaset lat podchodzono do liczb zespolonych, bo tak się one nazywają.
"Nie możemy zrozumieć, co to jest √-3? No, to nie próbujmy, ale posługujmy się takimi tworami"... Najpierw nauczmy się algorytmu, a może kiedyś, po dwustu latach, zrozumiemy. Dzisiaj (2015 r.) o liczbach zespolonych naucza się bez żadnej mistyki, w moim kąciku gościły one wielokrotnie i gdybym się nie rozpisał o przygodzie w autobusie, mógłbym tu wyłożyć całą ich teorię - na pewno znaną wielu Czytelnikom. Niewiele czasu potrzeba, by przynajmniej pobieżnie nauczyć się jej np. z odpowiedniej strony w Wikipedii.
1910: elipsa i asymptoty
Pomówmy o innym zadaniu, z matury w 1910 r., z Krakowa. Rok 1910... ładnie śpiewa o nim czeski bard Jaromir Nohavica w "piosence cieszyńskiej". Ale oto i zadanie:
Zadanie maturalne z 1910 r. Wyznaczyć równanie elipsy o dłuższej osi 6, wiedząc, że kąt między asymptotami tej elipsy jest równy 60 stopni.
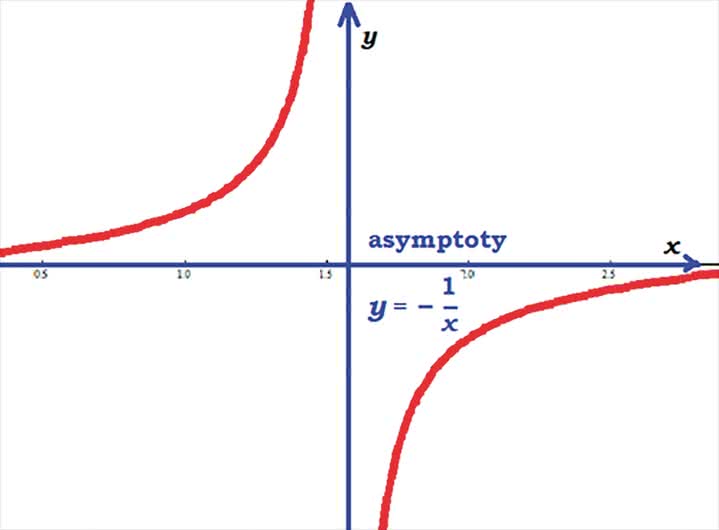
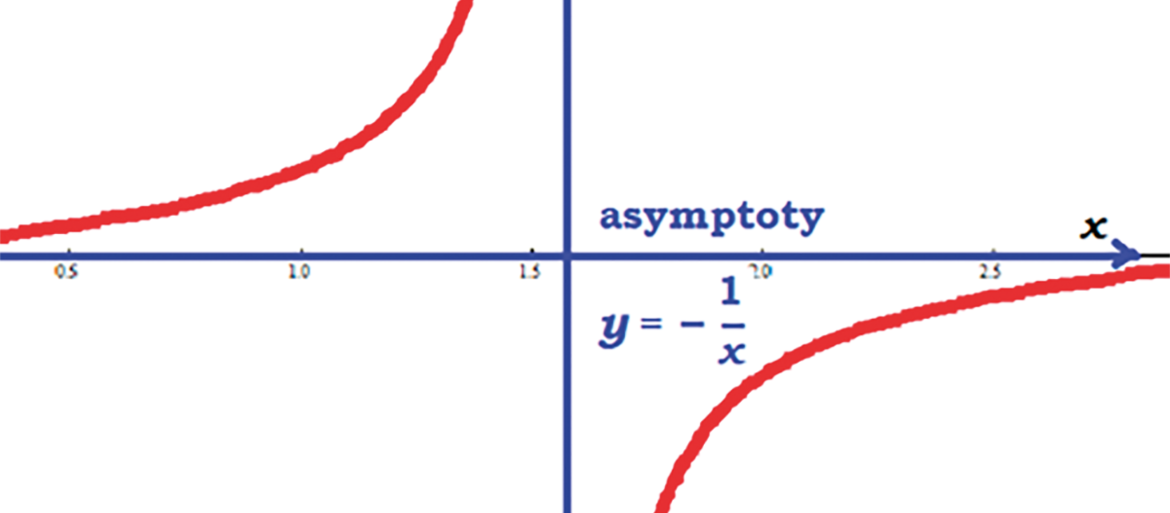
Oto krótki wykład, o co chodzi. Elipsę zna każdy - to takie spłaszczone koło (precyzyjniej: okrąg, czyli brzeg koła). Siedzący na trybunach kibice piłkarscy widzą koło środkowe boiska właśnie jako elipsę. Po orbitach eliptycznych poruszają się planety wokół Słońca. Z kolei słowo "asymptota" można zrozumieć jako linię prostą, do której nieograniczenie zbliża się dana krzywa. Nie jest to matematycznie poprawne określenie, ale wyjaśnia, o co chodzi. Najczęściej podawanym przykładem są asymptoty wykresu funkcji tangens albo hiperboli:
Z tego określenia każdy zrozumie, że niektóre krzywe asymptot nie mają - nie zbliżają się nieograniczenie do żadnej prostej. Sinusoida nieustannie zmienia kierunek, okrąg "kręci się w kółko", parabola wprawdzie "dąży w jednym kierunku", ale trudno o jej osi powiedzieć, że jest asymptotą - parabola oddala się od niej, a nie zbliża.
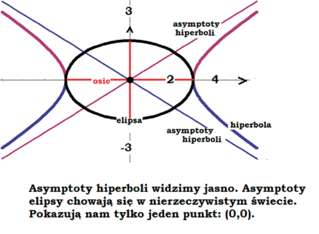
Czy zatem zadanie maturalne z 1910 r. jest źle ułożone? Nie, występujący w zadaniu termin "asymptoty elipsy" można rozumieć trojako. Albo że są to prawdziwe asymptoty hiperboli "przyklejonej" do danej elipsy, takiej jak na rysunku (2), albo - bardzo algebraicznie - jako tzw. kierunki główne, albo (i tak na pewno musieli to znać uczniowie z początków zeszłego stulecia) w następujący sposób: asymptoty hiperboli o równaniu
to dwie proste o równaniach powstających z zależności
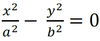
, a zatem
Zwróćmy uwagę, że asymptoty "celują w nieskończoność", w tym kierunku, do jakiego dąży hiperbola. Asymptoty elipsy o równaniu
wyznaczamy z podobnej zależności, tylko ze znakiem plus, tj.
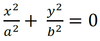Co otrzymujemy z tego równania. Cóż:
To samo, tylko... trochę inaczej. Asymptoty te są "nierzeczywiste", nie ma ich w naszym świecie. Pojawiają się dopiero wtedy, gdy zwiększymy zakres liczbowy. Czy to rozumiał doskonale uczeń sprzed stu lat? Może i... tak. Ładnie jest to opisane w powieści Roberta Musila "Niepokoje wychowanka Törlessa". Tytułowy bohater, uczeń gimnazjum pruskiego w Wielkopolsce, ma kłopoty egzystencjalne, w tym lęk przed liczbami zespolonymi, czyli właśnie przed pierwiastkami z liczb ujemnych.
Wracajmy do matury 1910. Nasz uczeń powinien napisać tak:
Niech równaniem elipsy będzie
Wiem, że dłuższa oś to 2a; zatem a = 3. Wiem, że tangens połowy kąta między asymptotami jest równy
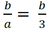Ponieważ żyję w roku 1910, a nie 2010, to wiem bez tablic, kalkulatora i Wikipedii, i całego Internetu, że tangens kąta 30 stopni jest równy
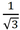Z tego samego powodu (że mamy rok 1910, a nie 2010), nie przedstawia dla mnie żadnej trudności obliczenie, że b =i proszę, by się nie przyczepiać, że może być także b = , bo nie ma to wpływu na równanie elipsy, którym jest
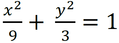Żałuję, że nie mam komputera i drukarki - może za sto lat narysowanie takiej elipsy będzie sprawą naciśnięcia kilku klawiszy maszyny do pisania. Tyle nasz uczeń - ja (2015 r.) mam komputer i drukarkę, choć jeszcze nie 3D. Oto ten wykres (rys. 2).
2016: coś na koniec i początek
A na nowy rok polecam takie oto zadanie matematyczne:
Pewna liczba ma w systemie pozycyjnym o podstawie dwucyfrowej ab postać ab00. Jaka to liczba w układzie dziesiętnym?
I tyle na nowy rok, tak ładnie rozkładający się na czynniki pierwsze: 2016=25·32·7.
