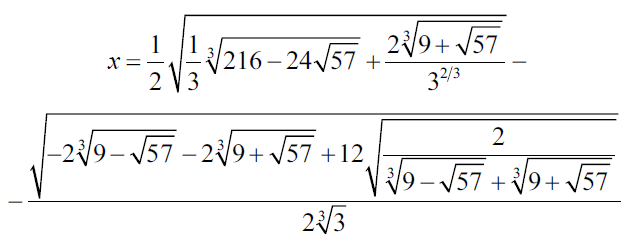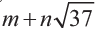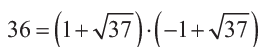Nagroda Abela

Choć matematycy bardziej cenią tzw. Medal Fieldsa (oficjalnie uważany na najwyższy laur we własnej dziedzinie), to jednak wiąże się z nim tylko 15 tys. (nie milionów, tysięcy!) dolarów kanadyjskich, podczas gdy zdobywcy Nagrody Abela wsuwa się do kieszeni czek na 6 mln koron norweskich (ok. 750 tys. euro). Nobliści dostają 8 mln SEK, czyli jakieś 865 tys. euro – mniej niż tenisiści za wygranie dużego turnieju. Jest kilka prawdopodobnych powodów, dla których Alfred Nobel nie uwzględnił matematyków jako ewentualnych biorców nagrody. Wola Nobla dotyczyła „wynalazków i odkryć”, przynoszących ludzkości największe korzyści, ale prawdopodobnie nie teoretyczne a praktyczne. Matematyka nie była uważana za naukę, która może przynieść ludzkości praktyczne korzyści.

Dlaczego Abel

Kim był Niels Henrik Abel i czym się wsławił? Musiał być genialny, bo choć zmarł na gruźlicę w wieku zaledwie 27 lat, to zdążył zaistnieć na stałe w matematyce. Otóż już w gimnazjum uczą nas rozwiązywać równania; najpierw pierwszego stopnia, potem kwadratowe i niekiedy sześcienne. Już czterysta lat temu uczeni włoscy dawali sobie radę z równaniem czwartego stopnia, choćby i takim, wyglądającym niewinnie:

a którego jednym z pierwiastków jest

Tak, to umieli uczeni już w XVI wieku. Nietrudno zgadnąć, że wzięto się więc za równania wyższych stopni. I… nic. Przez dwieście lat nikomu się nie udawało. Nie udało się również Nielsowi Abelowi. I wtedy zrozumiał, że… może w ogóle się nie da. Że można udowodnić niemożliwość rozwiązania takiego równania – a ściślej, wyrażenia rozwiązania prostymi wzorami arytmetycznymi.

To było pierwsze od 2 tys. lat (!) rozumowanie tego typu: coś się nie da udowodnić, czegoś się nie da zrobić. Na takie dowody monopol ma matematyka – nauki praktyczne coraz to łamią bariery. W 1888 r. przewodniczący Komisji Patentowej USA oświadczył, że „niewielu wynalazków należy się spodziewać w przyszłości, ponieważ prawie wszystko zostało już wynalezione” (everything has been invented). Dziś trudno się nam nawet z tego śmiać… A w matematyce – raz dowiedzione, przepadło. Nie da się i już.

Historia dzieli odkrycie, które opisałem, między Nielsa Abela i Evarysta Galois, obaj jako „wybrańcy bogów” zmarli przed trzydziestką, niedoceniani przez współczesnych. Niels Abel jest jednym z niewielu matematyków norweskich o szerokiej sławie (właściwie dwóch, drugi to Sophus Lie, 1842-1899 – nazwiska nie brzmią skandynawsko, ale obydwaj byli rdzennymi Norwegami).

Norwegowie są skłóceni ze Szwedami – niestety, rzecz to część częsta wśród sąsiadujących narodów. Jednym z motywów ustanowienia nagrody Abela przez Norwegów była właśnie chęć pokazania rodakom Alfreda Nobla: o proszę, my nie gorsi.

Pogoń za nieistniejącym zapiskiem na marginesie

Tyle o Nielsie Henriku Abelu. Teraz o zdobywcy nagrody, 63-letnim Angliku (mieszkającym w USA). Jego wyczyn z 1993 r. można porównać jedynie do wejścia na Everest, zdobycia Księżyca czy coś w tym rodzaju. Kim jest sir Andrew Wiles? Gdyby patrzeć na listę jego publikacji i różne możliwe indeksy cytowań, byłby dobrej klasy uczonym – jakich tysiące. Mimo to uznawany jest za jednego z najwybitniejszych matematyków. Jego badania dotyczą teorii liczb i używają związków z geometrią algebraiczną oraz teorią reprezentacji.

Sławę przyniosło mu rozwiązanie zupełnie nieistotnego z punktu widzenia matematyki problemu, jakim był dowód Wielkiego Twierdzenia Fermata (kto nie wie, o co chodzi – przypominam niżej). Jednak rzeczywistą wartością było nie samo rozwiązanie, a stworzenie nowej metody badania, która znalazła zastosowanie w rozwiązaniu wielu innych ważnych problemów.

Nie sposób nie zadumać się w tym momencie nad znaczeniem pewnych spraw, nad hierarchią ludzkich osiągnięć. Setki tysięcy młodych ludzi marzy o tym, by kopnąć piłkę lepiej niż inni, dziesiątki tysięcy chcą wystawiać się na himalajskie wiatry, skakać z gumy na moście, wydobywać z siebie dźwięki, które nazywają śpiewem, wpychać w innych niezdrowe jedzenie… albo rozwiązać nikomu niepotrzebne równanie. Pierwszy zdobywca Mount Everestu, sir Edward Hillary, odpowiedział prosto na pytanie, po co tam wszedł: „Bo on jest, bo Everest jest!” Piszący te słowa był przez całe życie matematykiem, taka była moja recepta na życie. Jedyna słuszna! Ale skończmy z tą filozofią. Wracajmy na zdrową ścieżkę matematyki. O co było tyle hałasu z twierdzeniem Fermata?

Zakładam, że wszyscy wiemy, co to są liczby pierwsze. Na pewno zwrot „rozłożyć na czynniki pierwsze” rozumie każdy, szczególnie, gdy nasz mały synek rozkręci zegar na części.

Pierre de Fermat (1601-1665) był prawnikiem z Tuluzy, ale zajmował się też amatorsko matematyką i to z zupełnie dobrym skutkiem, gdyż przeszedł do historii matematyki jako autor wielu twierdzeń teorii liczb i analizy. Miał zwyczaj umieszczania swych uwag i komentarzy na marginesach czytanych książek. No i właśnie – ok. 1660 r. napisał na jednym z marginesów: jest niemożliwe, by rozłożyć sześcian na dwa sześciany, czwartą potęgę na dwie czwarte i ogólnie potęgę wyższą niż druga na dwie takie potęgi; znalazłem naprawdę zadziwiający dowód tego twierdzenia, jednak margines jest za mały, by go pomieścić.

Tyle Pierre de Fermat. Od jego czasów (a przypomnę, że we Francji żył wtedy dzielny szlachcic gaskoński d’Artagnan, a w Polsce Andrzej Kmicic zmagał się z Bogusławem Radziwiłłem) setki, a pewnie i tysiące wielkich i małych matematyków próbowało bezskutecznie zrekonstruować zaginione rozumowanie genialnego dyletanta. Choć dziś jesteśmy pewni, że dowód Fermata nie mógł być prawdziwy, irytującym było, że tak prosto formułujące się pytanie: czy równanie xⁿ + yⁿ = zⁿ, n > 2 ma rozwiązania w liczbach naturalnych? może być aż tak trudne.

Wielu z matematyków, którzy przyszli 23 czerwca 1993 r. do pracy, zastało w swojej poczcie elektronicznej (będącej podówczas świeżym, jeszcze ciepłym wynalazkiem) lakoniczną wiadomość „Rumours from Britain: Wiles proves Fermat”, czyli: „Pogłoski z Brytanii: Wiles dowodzi Fermata”. Następnego dnia pisała o tym i prasa codzienna, a ostatni z cyklu wykładów Wilesa zgromadził prasę, telewizję i fotoreporterów – zupełnie jak na konferencji znanego piłkarza.

Kto czytał „Szatana z siódmej klasy” Kornela Makuszyńskiego, ten z pewnością pamięta, czym zajmował się pan Iwo Gąsowski, brat profesora historii, którego system odpytywania uczniów odkrył Adaś Cisowski. Iwo Gąsowski rozwiązywał właśnie równanie Fermata, tracąc czas, majątek i zaniedbując dom: Wstawał późno, gdyż pracował długo w noc, grzmiąco pokrzykując wśród nocnej ciszy, bardzo mu to bowiem pomagało do myślenia. Każdej nocy był bliski piorunującego zwycięstwa i każdego dnia zjawiał się kwaśny, ponury i skrzywiony jak błędny rachunek...

W końcu pan Iwo zrozumiał, że rachunkami na potęgach nie zapewni szczęścia rodzinie i dał spokój. Makuszyński nie lubił nauki, ale w stosunku do pana Gąsowskiego miał rację. Iwo Gąsowski popełniał jeden zasadniczy błąd. Nie próbował stać się specjalistą w dobrym sensie tego słowa, tylko działał jak amator. Andrew Wiles jest zawodowcem.

Historia zmagań z Wielkim Twierdzeniem Fermata jest interesująca. Dość prosto da się zauważyć, że wystarczy je rozwiązywać dla wykładników będących liczbami pierwszymi. Dla n=3 rozwiązanie podał w 1770 r. Leonhard Euler, dla n=5 – Peter Gustav Lejeune Dirichlet (1828) i Adrien Marie Legendre w 1830 r., a dla n=7 – Gabriel Lamé w 1840 r. W XIX wieku najwięcej energii problemowi Fermata poświęcił matematyk niemiecki Ernst Eduard Kummer (1810-1893). Choć nie uzyskał ostatecznego sukcesu, dowiódł bardzo wielu szczególnych przypadków i odkrył wiele ważnych własności liczb pierwszych. Duża część współczesnej algebry, arytmetyki teoretycznej i algebraicznej teorii liczb zawdzięcza swoje powstanie pracom Kummera nad twierdzeniem Fermata.

Przy atakowaniu zagadnienia Fermata metodami klasycznej teorii liczb rozbijano je na dwa różne co do trudności przypadki: pierwszy, gdy zakładamy, że iloczyn xyz jest względnie pierwszy z wykładnikiem n i drugi, gdy liczba z jest podzielna przez wykładnik. W przypadku drugim wiadomo było, że rozwiązań nie ma aż do wykładnika n=150 000, w pierwszym aż do n=6 000 000 000 (Lehmer, 1981). Wynikało stąd, że ewentualny kontrprzykład byłby i tak nie do osiągnięcia: jego otrzymanie wymagałoby rachunków na liczbach o miliardach cyfr.

Tyle dawna historia. W początkach 1988 r. świat matematyczny obiegła wiadomość, że Yoichi Miyaoka udowodnił pewną nierówność, z której wynikało, co następuje: jeżeli tylko wykładnik n jest dostatecznie duży, to równanie Fermata na pewno nie ma rozwiązań. W zestawieniu z nieco wcześniejszym wynikiem Niemca Gerda Faltingsa (1983) rezultat Miyaoki znaczył, że jeżeli rozwiązania są, to jest ich (z dokładnością do proporcjonalności) tylko skończenie wiele. W ten sposób rozstrzygnięcie zagadnienia Fermata zostało sprowadzone do wyliczenia skończenie wielu przypadków. Niestety, nie wiadomo było, jak wielu: metody użyte przez Miyaokę nie dawały możliwości oszacowania, od której liczby n już „jest dobrze”.

Warto tu zwrócić uwagę, że od wielu lat badania nad twierdzeniem Fermata prowadzone były nie w ramach czystej teorii liczb, lecz geometrii algebraicznej, dyscypliny matematycznej wywodzącej się z algebry i będącej rozwinięciem kartezjańskiej geometrii analitycznej, a wciskającej się obecnie niemal wszędzie: od podstaw matematyki (teoria toposów w logice), poprzez analizę matematyczną (metody kohomologiczne, snopy funkcyjne), klasyczną geometrię, do fizyki teoretycznej (wiązki wektorowe, przestrzenie twistorowe, solitony).

Gdy na honorach nie zależy

Trudno przy okazji nie zasmucić się nad losem matematyka, którego wkład w rozwiązanie problemu Fermata jest bardzo znaczący. Mowa o Arakiełowie (Suren Jurijewicz Arakiełow, matematyk ukraiński o korzeniach ormiańskich), który we wczesnych latach 80. ub. stulecia, gdy był na IV roku studiów, stworzył tzw. teorię przecięć na rozmaitościach arytmetycznych. Takie powierzchnie są pełne dziur i niezupełności, a krzywe na nich mogą jak gdyby nagle znikać i potem pojawiać się na nowo. Teoria przecięć wyjaśnia, jak obliczać stopnie przecięcia takich krzywych. Była ona podstawowym narzędziem używanym w pracach Faltingsa i Miyaoki, zahaczającym o problem Fermata.

Pewnego roku Arakiełow został zaproszony do przedstawienia swoich wyników na dużym kongresie matematycznym. Ponieważ jednak krytykował ustrój radziecki, nie uzyskał zgody na wyjazd. Wkrótce potem otrzymał wezwanie do wojska. W demonstracyjny sposób wyjaśniał, że jest przeciwny służbie wojskowej w ogóle, ze względów pacyfistycznych. Jak dowiedziałem się z dość niepewnych źródeł, podobno skierowano go do zamkniętego szpitala psychiatrycznego, w którym spędził około roku. Jak powszechnie wiadomo, najwyraźniej do celów politycznych, radzieccy psychiatrzy wyodrębnili specjalny rodzaj schizofrenii (po angielsku sluggish schizophrenia, od sluggish, czyli „ospały”, po rosyjsku вялотекущая шизофрения).

Trudno powiedzieć na sto procent, jak było naprawdę, bo moje źródła informacji nie są bardzo wiarygodne. Podobno po wyjściu ze szpitala Arakiełow spędził kilka miesięcy w klasztorze w Zagorsku. Obecnie żyje w Moskwie z żoną i trójką dzieci. Matematyką się nie zajmuje. Andrew Wiles opływa zaś w zaszczyty i pieniądze.

Z punktu widzenia sytego społeczeństwa europejskiego, niezrozumiały jest też krok Grigorija Perelmana, który w 2002 r. rozwiązał najsłynniejszy problem topologiczny dwudziestego wieku, „hipotezę Poinarego”, po czym odrzucał wszelkie możliwe przyznawane mu nagrody. Najpierw wspominany na początku Medal Fieldsa, co matematycy traktują jako równoważnik Nagrody Nobla, a następnie wartą okrągły milion dolarów nagrodę za rozwiązanie jednego z siedmiu najważniejszych problemów matematycznych, jakie zostały jeszcze z XX wieku. „Inni byli lepsi, na honorach mi nie zależy, bo matematyka to moje hobby, na jedzenie i papierosy mam” – tak mniej więcej oświadczył zdumionemu światu.

Sukces po ponad 300 latach

Wielkie twierdzenie Fermata było z pewnością najsłynniejszym i najbardziej efektownym zagadnieniem matematycznym. Otwarte było przez ponad trzysta lat, formułuje się w sposób bardzo jasny i czytelny i było teoretycznie możliwe do zaatakowania przez każdego, a w dobie upowszechnienia komputerów można było stosunkowo łatwo starać się o pobicie kolejnego rekordu oszacowania ewentualnych rozwiązań. W historii matematyki zagadnienie to, poprzez swą inspirującą rolę, odegrało bardzo ważną rolę „kulturotwórczą”, przyczyniając się do powstania całych dyscyplin matematycznych. Jest to o tyle dziwne, że sam problem jest stosunkowo błahy i sama informacja o braku pierwiastków równania Fermata nie wniosła wiele do ogólnej skarbnicy wiedzy matematycznej.

W 1847 r. Gabriel Lamé (1795-1870) wygłosił referat we francuskiej Akademii Nauk, ogłaszając rozwiązanie zadania Fermata. Jednakże subtelny błąd rozumowania dostrzeżono natychmiast. Polegał na nieuprawnionym stosowaniu twierdzenia o jednoznacznym rozkładzie. Pamiętamy ze szkoły, że każda liczba ma jednoznaczny rozkład na czynniki pierwsze, np. 2012=2∙2∙503. Liczba 503 nie ma już dzielników (poza liczbą 1 i samą 503), rozłożyć dalej więc się nie da.

Własność jednoznacznego rozkładu przysługuje liczbom całkowitym dodatnim, ale wśród innych zbiorów liczbowych nie musi tak być. Przykładowo, dla liczb postaci

mamy 36 = 2²⋅2³ ,ale również

Analizując dowód Lamégo, Kummer zdołał wykazać prawdziwość przypuszczenia Fermata dla pewnych wykładników p. Nazwał je właśnie liczbami pierwszymi regularnymi. To był pierwszy istotny krok w kierunku pełnego dowodu. Wokół twierdzenia Fermata narastał mit. „A może to jest jeszcze gorzej – może nawet nie można udowodnić, że się da lub nie da rozwiązać?”

Ale od lat 80. zeszłego wieku wszyscy czuli, że cel jest blisko. Pamiętam, że jeszcze stał mur berliński, a ja już słuchałem wykładów o tym, że „już zaraz, za chwilę”. No cóż, ktoś musiał być pierwszy. Andrew Wiles zakończył swój wykład z angielską flegmą: „Sądzę, że to dowodzi Fermata”, a do wypełnionego poza granice możliwości audytorium dopiero po pewnym czasie dotarło, co się stało: oto padł 330-letni problem matematyczny, którym zajmowały się intensywnie setki matematyków z najwyższej półki i niezliczona rzesza amatorów, jak choćby Iwo Gąsowski z powieści Makuszyńskiego. A Andrew Wiles dostąpił zaszczytu uściśnięcia ręki Haraldowi V, królowi Norwegii. Na skromny dodatek do Nagrody Abela, rzędu kilkuset tysięcy euro, może nie zwrócił uwagi – po co mu aż tyle pieniędzy?