Uczyć inaczej (ale czy warto?)
Nie będę zanudzać Czytelników dyskusją dydaktyczną na ów temat. W matematyce zawsze się rozwiązywało, rozwiązuje i będzie rozwiązywać zadania. Tego przede wszystkim uczymy naszych uczniów. I słusznie - bo tego wymagamy potem od nich przy egzaminach. Wypełniając im w ten sposób czas, zapominamy jednak o innych, ważnych sprawach. O rozumieniu, czytaniu ze zrozumieniem, analizowaniu i... uważnym patrzeniu. Co rozumiem przez "uważne patrzenie"?
Mogę je określić jako "patrzenie antytelewizyjne". W telewizji pokazują nam obrazek na kilka sekund, zaraz potem drugi, trzeci, czwarty... - ważna jest ich liczba, nieważne, co na nich widać. Tempo, liczy się tempo i zmienność. Nawet na spotkaniach towarzyskich panuje podobna moda na pokazywanie slajdów z wakacji: kilkaset zdjęć w pół godziny.
I oto pierwszy, charakterystyczny przykład. Tego, jak bym chciał nauczać matematyki. Może ktoś spróbuje?
Jak bym chciał nauczać
"Narysujcie, uczniowie, dowolny czworokąt, wypukły. Połączcie odcinkami środki kolejnych boków. Co widzicie? Tak, Michał ma rację - powstał równoległobok. Czy u każdego pojawił się równoległobok? A czy potraficie udowodnić, że tak zawsze będzie? No, jasne, Agnieszka do tablicy... Masz rację, wystarczy dorysować przekątne czworokąta i wszystko jasne."
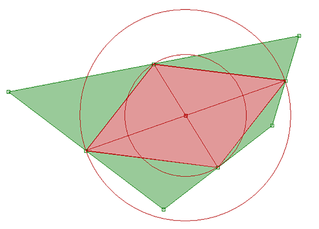
Na zwykłych lekcjach byłby to koniec tematu. U mnie początek. Mówię następnie: "Spójrzcie na rysunek (po lewej) i ułóżcie jakieś zadanie, związane z nim. Tak, z tym rysunkiem. Jedno właśnie rozwiązywaliśmy - po połączeniu środków boków powstał równoległobok. Jak to jakie zadanie? Nie rozumiesz - masz ułożyć, stworzyć zadanie."
Z moich doświadczeń wynika, że uczniowie nie wychodzą poza zadania w rodzaju "oblicz pole tego równoległoboku, oblicz obwód" itp. Nie rozumieją też, co nazywam problemem (twierdzeniem) odwrotnym. Wyjaśniam to tak: "Masz dany równoległobok (różowy na rys. 1). Czy możesz dorysować do niego czworokąt tak, by ten równoległobok był równoległobokiem środków? A czy na jeden sposób, czy na więcej? Co mają wspólnego ze sobą te sposoby?"
Staram się pokazywać uczniom to wszystko w ruchu. Nie znam się na Geogebrze, używam innych programów, ale słyszałem - ona wszystko wyrysuje, w animacji. A zatem zadaję uczniom takie zadanie (gdy przerabiam je z nauczycielami, daję dosłownie takie polecenia, jak napisałem niżej - z uczniami staram się być bardziej poważny).
Zachwyty i dziwy
Zadanie na programy Cabri, Geogebra, C.a.R. itp. (uwaga: bez tych programów też większość tych poleceń ma sens).
- Narysować zielony (może być inny zimny kolor) czworokąt.
- Zaznaczyć środki boków.
- Połączyć środki kolejnych boków odcinkami; zaznaczyć otrzymany tak czworokąt ciepłym kolorem.
- Animować rysunek i wznosić okrzyki zachwytu, że czworokąt zmienia kształt, a wewnątrz równoległobok jak był, tak i jest.
- Dorysować przekątne tego równoległoboku i zaznaczyć ich punkt przecięcia.
- Narysować okręgi o środku w punkcie przecięcia przekątnych równoległoboku środków, przechodzące przez przeciwległe wierzchołki.
- Ruszać wierzchołkiem czworokąta i dziwować się w głos, jak się te okręgi zmieniają.
- Postawić problem, kiedy okręgi te się pokryją.
- Umiejscowić cały rysunek na siatce, wybrać dogodne współrzędne.
- Animując całą sytuację (jak w pkt. 4), odgadnąć warunek konieczny i dostateczny na to, by równoległobok środków był prostokątem. A kwadratem? Zapamiętać (zanotować) hipotezę i odłożyć do sprawdzenia w drugiej części zajęć.
- Obejrzeć, co się dzieje, gdy czworokąt wyjściowy degeneruje się do trójkąta. Zaproponować zadania dotyczące tej sytuacji.
Czy spodziewałeś się, Czytelniku, że z tak banalnej własności da się zrobić cały pakiet zagadnień do dyskusji? A to nie koniec. Teraz rzucam pytanie: "Czy potraficie uogólnić tę własność?". Na ogół nikt nic nie wie, więc naprowadzam: "No, to weźmy trójkąt zamiast czworokąta. Jak to będzie w trójkącie? Dobrze, Oliwio, ten mały trójkąt będzie podobny do dużego. Czy wszyscy pamiętają, co to są trójkąty podobne? A w jakiej skali?"
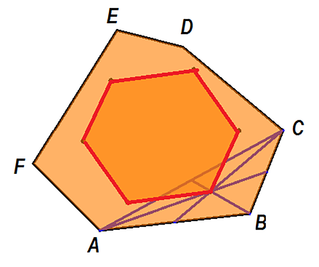
Mówię dalej: "To weźmy pięciokąt..." Po dłuższej chwili wszyscy spostrzegają, że... nic nie widać. Bo teraz jest już trudniej. Biorę sześciokąt, rzucam rysunek:
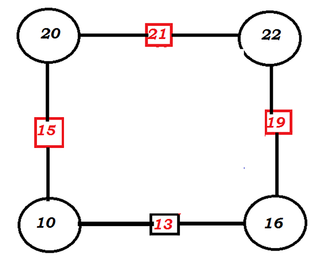
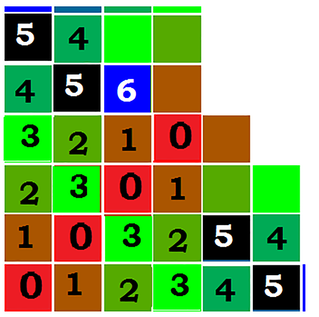
Ale tylko licealiści są w stanie zgadnąć kryjące się za tym twierdzenie i nawet uogólnić je na wielokąty o większej liczbie boków. Gdy już wszyscy wydają się zmęczeni tym tak wałkowanym zagadnieniem, przechodzę do arytmetyki: pokazuję kwadrat liczbowy, np. taki:
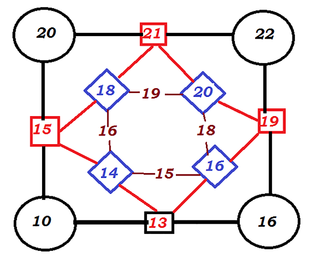
Wyjaśniam, że liczby stojące w środkach boków są średnimi arytmetycznymi liczb wierzchołkowych. Przechodzę do bardzo trudnego zagadnienia: "Czy widzicie, że to jest zadanie izomorficzne (tak naprawdę nie używam tego słowa) z poprzednim?" "Jak to, to przecież co innego, tam była geometria, a tu arytmetyka..." - protestują uczniowie, a ja przypomnę, że każdy nauczyciel spotkał się z taką sytuacją: "Nie, nie pszepani, to zupełnie inne zadanie - tamto do domu było o cukierkach, a to na klasówce o czekoladkach!".
Mam zatem temat na dalszą długą dyskusję - przetłumaczyć wszystkie pytania z sytuacji geometrycznej na arytmetyczną, odpowiedzieć na wszystko, a w szczególności: "Czy dla zadanych średnich arytmetycznych można odzyskać wyjściowe liczby? Czy jednoznacznie? Co dla trójkątów, pięciokątów, sześciokątów liczbowych?"
Gdy już wszyscy "mają dość", rzucam następne pytania: "A gdy weźmiemy inne średnie?" Ale nie nalegam i gdy mam do czynienia z licealistami albo nauczycielami, zadaję jeszcze jedno pytanie (i wtedy znowu się ożywiają): "No, to iterujmy postępowanie. Róbmy tak dalej, średnie ze średnich, średnie średnich średnich... Masz rację, Patryku, weźmy komputer. Umiecie już Excela, prawda? No, to proszę, zaprogramujcie taki zagnieżdżający się układ , powiedzmy do dziesiątego piętra, czyli żeby było dziesięć zagnieżdżających się kwadratów. Weźcie jakieś liczby wyjściowe, bawcie się nimi. Obserwujcie tylko wyniki."
No i już gotowy temat na pierwszą pracę naukową, na początek bardzo skromną. Ale, ale... wróćmy znów do geometrii. Co nam wyjdzie, jeżeli będziemy powtarzać naszą konstrukcję, w głąb i w głąb... To zadanie dla Czytelników. A ja zwrócę tylko uwagę na to, że wyszliśmy z łatwego i pozornie nieciekawego zadania... i zobaczyliśmy w nim znacznie więcej. To:
Zadania otwarte na zmiany
Na przykładzie dwóch zadań powiem, jak można by nauczać inaczej. Przyzwyczajeni jesteśmy do tego, że matematyka to taki ciąg: nauczyciel zadaje zadanie, uczeń rozwiązuje, nauczyciel omawia i... zadaje następne zadanie. Matematyka jako ciąg: zadanie-rozwiązanie- zadanie- rozwiązanie... Czy w ogóle można inaczej?
Można. Ale to sprawa trudna, wymaga innego spojrzenia na proces nauczania. A oto drugie zadanie, otwarte. Wziąłem je z zestawu zadań przygotowawczych do pewnych warsztatów matematycznych o zasięgu europejskim, miało tam numer 8 (http://goo.gl/lsnBm9).
Numerujemy pola szachownicy, rozciągającej się w nieskończoność w górę i w prawo. Zaczynamy numerację od zera. W zerowym wierszu i zerowej kolumnie (to znaczy w lewym dolnym narożniku) stawiamy 0, a następnie w każdym innym polu stawiamy najmniejszą liczbę (nieujemną, całkowitą), która nie pojawia się ani na lewo, ani poniżej tego pola, o tak:
Jaka liczba będzie stać w kwadracie w wierszu numer 2016 i kolumnie numer 1601? Can you generalize? Zostawiłem, dla uwypuklenia, ostatnie zdanie po angielsku. Znaczy ono: "Czy potrafisz uogólnić?" To nazywam właśnie zadaniem otwartym - nie kończy się na rozwiązaniu. "Czy umiesz uogólnić?"
Stawiałem to i podobne pytania w różnych środowiskach uczniowskich, studenckich i nauczycielskich. Dzieci pytały, co to znaczy. Uczniowie ograniczali się do banalnych pytań i odpowiedzi. A nauczyciele rozumieli oczywiście, o co chodzi, ale oni, najbardziej przyzwyczajeni do zadań zamkniętych, nie byli w stanie zadać ani jednego sensownego pytania, zaproponować rozwinięcia enigmatycznego "uogólnij". Mówię oczywiście o statystycznych danych, a nie o dosłownie wszystkich uczniach, studentach i nauczycielach.
Cenię właśnie takie zadania, które dopuszczają możliwości zmian, interpretacji, uproszczeń i utrudnień, które mają wiele dróg dojścia do rozwiązania, które są dostępne niemal dla każdego, prowadzą w głąb matematyki, której tu nie nazywam "wyższą" a "uniwersytecką".
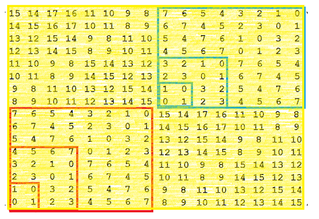
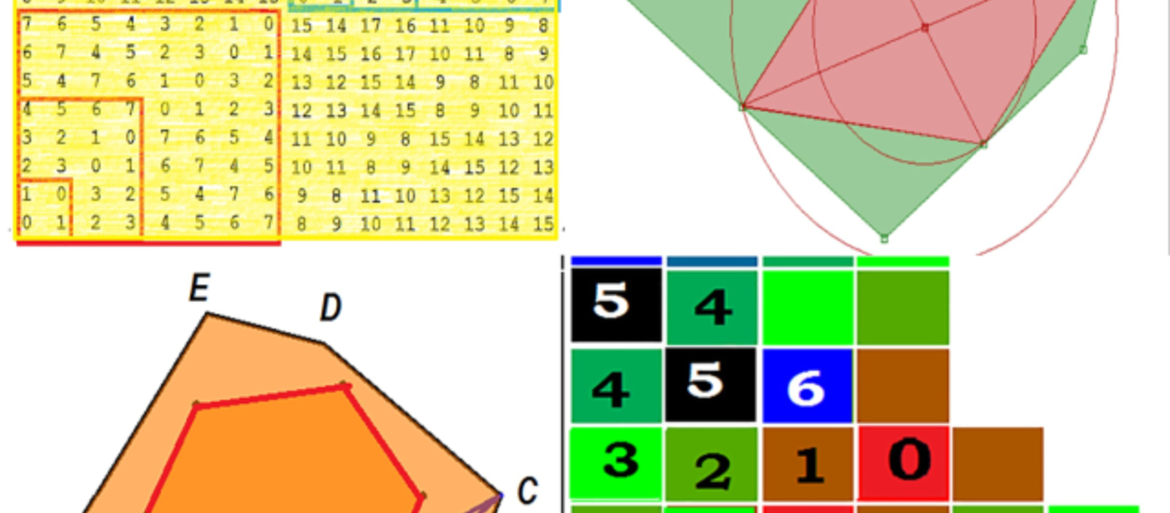
Najpierw rozwiązanie. Można ułożyć program, generujący kolejne pola. Ponieważ jednak pole, o które chodzi, ma kolejny numer 3227616, więc nieładnie ułożony program może po prostu "nie doliczyć się" do tego miejsca. Mamy zatem alternatywę: udoskonalić program, czy znaleźć ładne rozumowanie, prowadzące do celu. Jedno i drugie jest wartościowe. Ale z komputerem czy bez możemy rozszerzyć podany wzorzec - początek rozwiązania. I teraz już wszystko jasne. Trzeba tylko umiejętnie spojrzeć na otrzymane informacje.
Tablica ma układ blokowy. Bloki są kolejnych rozmiarów 2, 4, 8, 16, 32, ... - są to kolejne potęgi liczby 2. W każdej kolumnie i w każdym wierszu mamy permutację liczb od zera do 15. Na przekątnej mamy zera, nad przekątną jedynki. Na obrzeżach liczby od jedynki do 2n-1, w naszej tabelce od zera do 15. W każdym wierszu i każdej kolumnie mamy interesujące permutacje - ale o tym już nie pomówimy.
Obliczmy, ile bloków potrzeba, by dojść do 2016. Dzielimy 2016 przez 32. Starsze pokolenie potrafi bez kalkulatora. Wychodzi 63. I tu jeszcze jeden powód, dla którego lubię to zadanie i ten typ zadań. To tak, jak wycieczka, gdzie chodzi nie tylko o cel, ale i o ciekawe miejsca, które mija się po drodze. Cóż to jest 32 razy 63, czyli wartość wyrażenia 2n-1(2n-1) dla n=6? Obliczmy wartości tego wyrażenia dla n będących liczbami pierwszymi: n=2, 3, 5, 7, 11, 13, 17, ... Otrzymamy: 6, 28, 120, 496, 2016, 8128, 32640, 130816, 523776, 2096128. ... a to liczby doskonałe. Tak właśnie szkoła pitagorejska nazwała liczby równe sumie swoich dzielników (nie licząc samej liczby). Przykładowo, 496 dzieli się przez: 1, 2, 4, 8, 16, 31, 62, 124, 248, 496.
No a suma 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496. Twierdzenie Euklidesa-Eulera powiada, że wzór 2p-1(2p-1) daje wszystkie parzyste liczby doskonałe (p w tym wzorze ma być liczbą pierwszą). Istnienie nieparzystych liczb doskonałych jest nierozwiązanym problemem matematycznym, i to takim z gatunku "beznadziejnych" - na razie nikt nie ma pomysłu, jak się do tego zabrać. Na razie! Przyjdzie w końcu jednak ktoś, kto wymyśli!
Liczba 6 nie jest pierwsza, zatem 2016 nie jest liczbą doskonałą. Ma nawet więcej dzielników niż "potrzeba". Oto lista dzielników liczby 2016: 1, 2, 3, 4, 6, 7, 8, 9, 12, 14, 16, 18, 21, 24, 28, 32, 36, 42, 48, 56, 63, 72, 84, 96, 112, 126, 144, 168, 224, 252, 288, 336, 504, 672, 1008 Ich suma to 4536, znacznie więcej niż 2016. Z postaci 2p-1(2p-1) wynika jednak, że 2016 jest liczbą trójkątną: sumą kolejnych liczb od jedynki (albo od zera) do 63: 0 + 1 + 2 + 3 + 4 + 5 + 6 + ... + 59 + 60 + 61 + 62 + 63 = 2016
Przypomina to historyjkę o wynalezieniu szachów. Pisałem o niej wielokrotnie i nie będę się powtarzał. Odsyłam... do Internetu.
Mądrze się rozproszyć
Revenons á nos moutons. To francuskie zdanie znaczy dosłownie "wracajmy do naszych baranów", a prawdziwe znaczenie to mniej więcej: "wróćmy do rzeczy" (polecam zajrzenie do Wikipedii). Powróćmy do naszego zadania. I to lubię w zadaniach pewnego typu - że można się zagubić w dygresjach tak, że na samo zadanie nie wystarcza już ani czasu, ani cierpliwości. Przestaje nas interesować cel. Rozproszyliśmy się, rozmieniliśmy na drobne. Muszę przyznać, że ja to właśnie w zadaniu lubię, chociaż chyba to niepedagogicznie...
Rozpatrzmy bloki rzędu 5, to znaczy tablice 32 na 32. Południowo-wschodnim wierzchołkiem sześćdziesiątego trzeciego bloku jest 2015. Następna kolumna zaczyna się na 2016 i do połowy wysokości maleje aż do 1007. Potem startuje od zera, osiągając wartość 593 na poziomie, o który nam chodzi, to znaczy 1601. Zadanie rozwiązane! Ajaj, nie do końca. A co z pytaniem o uogólnienie? To już niech będzie kwestia do domu, dla Czytelników, na nadchodzące upały.