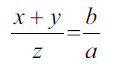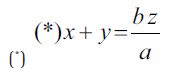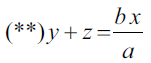Dlaczego nie dzielimy przez zero?

Z zerem, owszem, są w ogóle same kłopoty, wynikające z tego, że tak naprawdę nie potrzebujemy go używać w codziennym życiu. Nie idziemy do sklepu po zero jajek. „W pokoju jest jeden człowiek” brzmi jakoś naturalnie, a „zero ludzi” – sztucznie. Językoznawcy mówią, że zero znajduje się poza systemem językowym.

Możemy obyć się bez zera i w rachunkach bankowych: po prostu używając – jak na termometrze – koloru czerwonego i niebieskiego dla wartości dodatnich i ujemnych (zauważmy tylko, że dla temperatury naturalne jest użycie czerwonego dla liczb dodatnich, a dla rachunków bankowych – odwrotnie, bo debet powinien powodować alert, użycie czerwonego koloru jest więc jak najbardziej wskazane).

Przez zaliczenie zera do liczb naturalnych dotykamy problemu odróżniania liczb kardynalnych od porządkowych. W ciągu 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, .....
kardynalność liczby pokrywa się z numerem miejsca, na którym ona stoi. Inaczej jest już w ciągu 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, .....

Liczba opisująca zbiory jednoelementowe znajduje się tu na drugim miejscu, liczba opisująca zbiory o dwóch elementach na trzecim i tak dalej. Musimy tłumaczyć, dlaczego nie numerujemy np. miejsc sportowców w zawodach od zera. Wtedy zdobywca pierwszego miejsca dostawałby medal srebrny (złoty przypadałby zdobywcy miejsca zerowego) itp. Nieco podobny zabieg zastosowano u nas w piłce nożnej – nie wiem, czy Czytelnicy wiedzą, że „pierwsza liga” to znaczy „następna po najlepszej”, a ligę zerową nazywa się „ekstraklasą”.

Niekiedy słyszymy argumentację, że należy zaczynać od zera, bo tak jest wygodnie informatykom. Kontynuując to rozumowanie, należałoby zmienić określenie kilometra – powinien wynosić 1024 m, bo przecież tyle jest bajtów w kilobajcie (nawiązuję tu do znanego informatykom dowcipu: „Jaka jest różnica między studentem pierwszego roku informatyki a studentem piątego roku tego kierunku? Pierwszy z nich uważa, że kilobajt ma 1000 kilobajtów, ten drugi – że kilometr ma 1024 metry”)!

Inny pogląd, który już należy brać poważnie pod rozwagę, jest następujący: przecież mierzymy zawsze od zera! Wystarczy spojrzeć na dowolną podziałkę na linijce, na wadze domowej, nawet na zegarze. Skoro mierzymy od zera, a liczenie można rozumieć jako mierzenie jednostką niemianowaną, to i liczyć powinniśmy od zera.

Sprawa prosta, ale…

Porzućmy ogólną dyskusję i wróćmy do dzielenia przez zero. Sprawa jest prosta i byłaby prosta, gdyby nie… no właśnie, co? Zastanówmy się, popróbujmy. Ile to może być – jeden podzielone przez zero? Zobaczmy: 1/0 = x . Mnożymy obie strony przez mianownik lewej strony.
Otrzymujemy, że 1 = 0. Coś nie tak! Co nie tak? A, założenie! Założenie, że istnieje iloraz jedynki i zera, prowadzi do sprzeczności. A jeżeli jedynki nie można podzielić przez zero, to innej liczby też. Jeżeli, Czytelniku, wzruszasz ramionami i dziwisz się, dlaczego autor (czyli ja) pisze o takich banałach, to… bardzo się cieszę!

Na upartego dałaby się obronić formuła 0/0 = 0 , kłócąca się jednak z zasadą, że wynik z dzielenia liczby przez siebie samą jest równy jeden. Zupełnie, ale zupełnie czym innym są symbole właśnie takie, jak 0/0 , °/° i podobne w analizie matematycznej. Nie oznaczają one żadnej liczby, tylko są symbolicznym zapisem ilorazów ciągów pewnych typów.

W książce o elektrotechnice znalazłem ciekawe porównanie: dzielenie przez zero jest niebezpieczne jak prąd wysokiego napięcia. To celne: prawo Ohma mówi, że iloraz napięcia i oporu to natężenie: V=U/R. Gdyby opór był zerowy, przewodem popłynąłby prąd o teoretycznie nieskończonym natężeniu, paląc każdy możliwy przewodnik.

Ułożyłem kiedyś wiersz o niebezpieczeństwie dzielenia przez zero – na każdy dzień tygodnia. Pamiętam, że najbardziej dramatycznym dniem był czwartek, ale na całość mojej twórczości w tym zakresie szkoda miejsca.

Gdy podzielisz coś przez zero
Bardzo wczesnym poniedziałkiem,
Tydzień, co się stał dopiero,
Masz już nieudany całkiem.

Gdy we wtorek po kolacji,
Wstawisz zero w mianowniku
To ci powiem, nie masz racji,
Kiepski mój matematyku!

Gdy przez zero, przez przekorę,
Byś podzielić chciała w środę,
Będziesz mieć kłopoty spore,
W głowie siano masz i wodę!

Chodził z nami pewien Bartek.
Był na bakier z regułami.
Dzielił on przez zero w czwartek.
Już go nie ma między nami!

Jeśli chęć cię dziwna bierze,
By przez zero dzielić w piątek,
Powiem ja ci prosto, szczerze:
To weekendu zły początek.

Gdy zaś zerem gdzieś w sobotę
Dzielnik będzie twój (nie zaś dzielna)
Pod kościelnym klęknij płotem.
To pokuta twa niedzielna.

Jeśli zero chcesz pod kreskę,
Wstawić w święto przy niedzieli,
Przynieś kredę, czarną deskę.
Pisz: przez zero się nie dzieli!

Zero kojarzy się z pustką i nicością. Istotnie, przyszło ono do matematyki jako wielkość, która dodana do dowolnej nie zmienia jej: x + 0 = x. Ale obecnie zero figuruje w kilku innych znaczeniach, przede wszystkim jako początek skali. Jeżeli za oknem nie ma ani dodatniej temperatury, ani mrozu, to… jest zero, co nie znaczy, że temperatury w ogóle nie ma. Zabytek klasy zerowej to nie ten, który został dawno zburzony i go po prostu nie ma. Wprost przeciwnie – to coś jak Wawel, wieża Eiffela i Statua Wolności.

No, a znaczenie zera w systemie pozycyjnym trudno przecenić. Czy wiesz, Czytelniku, ile zer ma na swoim koncie bankowym Bill Gates? Ja nie wiem, ale chciałbym mieć połowę. Podobno to Napoleon Bonaparte zauważył, że ludzie są jak zera: nabierają znaczenia dzięki pozycji. W filmie Andrzeja Wajdy „Z biegiem lat, z biegiem dni” zaperzony malarz Jerzy wybucha: „Filister to zero, nihil, nic, nic, nihil, zero.” Ale zero może być dobre: „zerowe odchylenie od normy” znaczy, że wszystko idzie dobrze i tak trzymać!

Wróćmy do matematyki. Zero możemy bezkarnie dodawać, odejmować i mnożyć. „Przytyłam zero kilogramów” mówi Mania do Ani. „A to ciekawe, bo ja schudłam tyle samo” odpowiada Ania. Zjedzmy więc sobie sześć razy po zero porcji lodów, to nam nie zaszkodzi.

Przez zero dzielić nie możemy, ale zero możemy dzielić. Misa zawierająca zero pierogów może być łatwo rozdzielona między czekających na posiłek. Po ile dostanie każdy?

Zero nie jest dodatnie, ani ujemne. Jest za to zarówno liczbą niedodatnią, jak i nieujemną. Spełnia obie nierówności: x≥0 oraz x≤0. Zaprzeczeniem zdania „coś jest dodatnie” nie jest „owo coś jest ujemne”, lecz: „coś jest ujemne bądź równe zero”. Matematycy, wbrew regułom językowym, zawsze powiedzą, że coś „jest równe zero” a nie „zeru”. Na uzasadnienie tego zwyczaju mamy: gdyby formułę x = 0 czytać „iks równe zeru”, to x = 1 czytaliśmy „iks równe jednemu”, co by się może dało przełknąć, ale co z „x = 1534267”? Nie można również przypisać wartości liczbowej symbolowi 0⁰, ani podnosić zera do ujemnej potęgi. Natomiast pierwiastkować zero można do woli… i zawsze wynikiem będzie zero,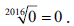 

Funkcja wykładnicza y = a^x, o podstawie dodatniej a, nie przyjmuje nigdy wartości zero. Wynika stąd, że nie istnieje logarytm zera. Istotnie, logarytmem liczby a przy podstawie b nazywamy wykładnik potęgi, do której należy podnieść podstawę, żeby otrzymać liczbę logarytmowaną a. Dla a = 0 takiego wykładnika nie ma, a także zero nie może być podstawą logarytmu. Natomiast czym innym jest zero w „mianowniku” symbolu Newtona. Przyjmujemy, że 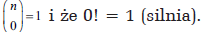Te umowy nie prowadzą do żadnej sprzeczności.

Fałszywe dowody

Dzielenie przez zero jest częstym motywem fałszywych dowodów i zdarza się to nawet doświadczonym matematykom. Przytoczę moje dwa ulubione przykłady. Pierwszy jest algebraiczny. „Udowodnię”, że wszystkie liczby są równe. Przyjmijmy, że są dwie liczby, które nie są równe. Jedna z nich jest zatem większa od drugiej, niech a > b. Przyjmijmy, że c jest ich różnicą
c = a – b. Mamy zatem a – b = c, skąd a = b + c .
Mnożymy obie strony tej ostatniej równości przez a – b:

a² – ab = ab + ac – b2 – bc.

Przenoszę ac na lewą stronę, o zmianie znaku oczywiście pamiętam:

a² – ab – ac = ab – b2 – bc.

Wyłączam wspólne czynniki:

A (a – b – c) = b (a – b –c),

Dzielę, no i mam, co chciałem:

a = b.

A właściwie jeszcze dziwniej, bo założyłem, że a > b, a dostałem, że a = b. O ile w powyższym przykładzie łatwo rozeznać się w „oszustwie” , to w poniższym dowodzie geometrycznym już nie tak prosto. Wykażę mianowicie, że… nie ma czegoś takiego, jak trapez. Figura zwana zwykle trapezem nie istnieje.

Rys. 1. Trapez

Przypuśćmy jednak najpierw, że jest coś takiego, jak trapez (ABCD na rysunku poniżej). Ma on dwa boki („podstawy”) równoległe. Przedłużmy te podstawy w sposób pokazany na rysunku tak, żeby utworzył się równoległobok. Jego przekątne dzielą drugą z przekątnych trapezu na odcinki, których długości oznaczymy przez x, y, z, jak na rysunku 1. Z podobieństwa odpowiednich trójkątów otrzymujemy proporcje:

skąd wyznaczamy:

oraz

skąd wyznaczamy:

Odejmujemy stronami równości oznaczone gwiazdkami: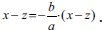

 Skracając obie strony przez x−z, otrzymujemy − a/b=1, czyli a + b = 0. Ale liczby a, b to długości podstaw trapezu. Jeżeli ich suma wynosi zero, to one same są również zerami. To znaczy, że nie może istnieć figura taka jak trapez! A ponieważ prostokąty, romby i kwadraty też są trapezami, zatem, drogi Czytelniku, nie ma również rombów, prostokątów ani kwadratów…

Zgaduj-zgadula

Dzielenie jest najciekawsze i najtrudniejsze z czterech podstawowych działań. Tu po raz pierwszy spotykamy się ze zjawiskiem, jakże częstym w dorosłym życiu: „zgadnij odpowiedź, a potem sprawdź, czy dobrze zgadłeś”. Ujmuje to bardzo trafnie Daniel C. Dennet („Jak popełniać błędy?”, w: „Jak to jest – naukowy przewodnik po Wszechświecie”, CiS, Warszawa 1997):

Cała sztuka polega na tym, by wykorzystać wiedzę o konsekwencjach swego ruchu i w następnej próbie nie strzelać już całkiem w ciemno. (...) W swojej najprostszej postaci jest to metoda, którą poznaliśmy już w szkole podstawowej. Przypomnij sobie, jak obco i groźnie wyglądało z początku dzielenie liczb wielocyfrowych: miałeś przed sobą dwie trudne do ogarnięcia liczby i musiałeś od czegoś zacząć. Czy dzielnik mieści się w dzielnej sześć, siedem, czy osiem razy? Kto to mógł wiedzieć? Nie trzeba było tego wiedzieć! Należało po prostu strzelać: wziąć dowolną liczbę na chybił-trafił i sprawdzić wynik. Pamiętam, że byłem wręcz zaszokowany, gdy powiedziano mi, że mam zgadywać. I to miała być matematyka? W tak poważnej sprawie nie ma chyba miejsca na zgadywanki? Ale wkrótce pojąłem piękno tej taktyki. Jeśli wybrana liczba okazywała się za mała, należało wziąć większą i zacząć od nowa; jeśli była zbyt duża, trzeba było rozpocząć od mniejszej. Najlepsze w dzieleniu liczb wielocyfrowych było to, że działanie to dawało zawsze dobry wynik, nawet gdy pierwszy wynik był maksymalnie chybiony – w takim wypadku zajmowało to jedynie trochę więcej czasu.

Taka metoda „zgadywania” nie przeszkadza nam w dojrzałym życiu – może dlatego, że uczymy się jej wcześnie, a zgadywanie nie jest trudne. Ideologicznie to samo zjawisko występuje np. przy indukcji matematycznej (zupełnej). Tam też „zgadujemy” wzór i potem sprawdzamy, czy nasze przypuszczenie było prawdziwe. Uczniowie zawsze pytają: „skąd mieliśmy wiedzieć, jaki jest wzór? Jak go można wyprowadzić?”. Gdy mi zadają to pytanie studenci, obracam ich pytanie w żart: „J a to wiem, bo jestem profesjonalistą, bo za to dostaję pensję, żebym w i e d z i a ł”. Uczniom w szkole można dać odpowiedź w tym samym stylu, tylko bardziej poważną.

Ćwiczenie. Zadumaj się nad tym, że dodawanie i mnożenie pisemne zaczynamy od jedności najniższego, a dzielenie od jedności najwyższego rzędu.

Zrost dwóch idei

Dydaktycy matematyki zawsze zwracali uwagę na to, że to, co w dorosłym życiu nazywamy dzieleniem, jest zrostem dwóch pojęciowo różnych idei: mieszczenia i podziału.

Pierwsza z nich (mieszczenie) występuje w zadaniach, których archetypem są:
Zeszyt kosztuje 4 centy. Ile zeszytów można kupić za 24 centy? (centy wziąłem z galicyjskiego podręcznika z 1891 r.);
W wazonie mieści się 5 kwiatów. Justyna chce wstawić 20 kwiatów. Ile wazonów potrzebuje?

Dzielenie-podział to zaś zadania takie jak:
Justyna chce wstawić 20 kwiatów do 4 wazonów. Po ile kwiatów zmieści się w jednym wazonie?
Robotnik w 4 tygodniach zarobił 26 złr., ile zarobił w jednym tygodniu? (zachowujemy oryginalny styl tego zadania, zaczerpniętego z poradnika Juliana Zgorzalewicza, wydanego w Krakowie, w 1892 r. – złr to złoty reński, waluta obiegowa w cesarstwie austro-węgierskim do początków XX wieku).

Rozważmy teraz dwa zadania z najstarszego podręcznika matematyki po polsku, księdza Tomasza Kłosa (1538). Czy chodzi tu o podział czy mieszczenie? Rozwiążcie to, jak przystało na uczniów w XXI wieku:
O ribach. Ieden karp za 5 kwartników. Wiele kop za 100 zło.
O winie nauka. Kwarth w barile á 4. garncze. 4 kwarty w garniecz. Ieden kupił na zysk kuphę wina: niesie 20. barił za 50 zło. Czło y phora koszt 8 zł. Po czemu ma szynkować 1. kwartę aby 8 zło. zyskać?

(Przekład z polskiego na polski: Baryłka ma kwartę i cztery garnce. Garniec to cztery kwarty. Ktoś kupił na handel 20 baryłek wina za 50 złotych. Cło i podatek (akcyza?) wyniosą 8 złotych. Po ile sprzedawać kwartę, aby zarobić 8 złotych?)

Sport, fizyka, kongruencja

W sporcie bywa, że trzeba podzielić coś przez zero (stosunek bramek). No, to jakoś sobie sędziowie z tym radzą. Natomiast w algebrze abstrakcyjnej na porządku dziennym są wielkości niezerowe, których kwadrat jest równy zero. Można to nawet prosto wytłumaczyć.

Rozważmy funkcję F, która punktowi płaszczyzny (x, y) przypisuje punkt (y, 0). Czym jest F², czyli podwójne wykonanie F? Funkcją zerową – każdy punkt ma obraz (0,0).

Wreszcie, wielkości niezerowe których kwadrat jest 0, to niemal chleb codzienny fizyków, a liczby postaci a + bε, gdzie ε ≠ 0, ale ε² = 0, matematycy nazywają liczbami dualnymi. Występują one w analizie matematycznej i w geometrii różniczkowej.

Mimo wszystko jest w arytmetyce coś, co przynajmniej w nazwie ma dzielenie przez zero. Bierze to się z kongruencji. Niech Z oznacza zbiór liczb całkowitych. Podzielenie zbioru Z przez p oznacza, że każdą liczbę (całkowitą) utożsamiamy z pewnymi innymi, a mianowicie z takimi, że ich różnica jest podzielna przez p. Zatem, gdy p = 5, mamy pięć typów liczb, odpowiadających liczbom 0, 1, 2, 3, 4 – możliwym resztom z dzielenia przez 5. Wzorem zapisuje się to tak:
m=n mod p, gdy różnica m – n jest wielokrotnością p.

Gdy p = 2, mamy tylko dwie liczby: 0 i 1. Podział liczb całkowitych na takie dwie klasy to podział ich na parzyste i nieparzyste. Podstawmy teraz. Różnica m – n jest zawsze podzielna przez 1 (każda liczba całkowita jest podzielna przez 1). A czy można wziąć p = 0? Spróbujmy: kiedy różnica dwóch liczb jest wielokrotnością zera? Tylko, gdy te dwie liczby są równe, m = n. A zatem podzielenie zbioru liczb całkowitych przez zero ma sens, ale nieciekawy: nic się nie dzieje. Należy jednak podkreślić, że nie jest to dzielenie liczb w sensie znanym ze szkoły podstawowej.

Takie działanie jest bowiem po prostu zakazane, jak matematyka długa i szeroka.

Rys. 2. Utożsamienie liczb za pomocą kongruencji
(mod 5 i mod 2)