Artykuł o Niczym

Ten artykuł miał więc być o pustce kosmicznej - a to z okazji lądowania europejskiego pojazdu na komecie 67P/Czuriumow-Gierasimienko 12 listopada 2014 r. Ale w trakcie pisania uległem wieloletniemu nawykowi, jestem przecież matematykiem. Jak to jest z Niczym, z Zerem w matematyce?

Jak istnieje Nic?

Nie można powiedzieć, że Nic nie istnieje. Ono istnieje co najmniej jako pojęcie filozoficzne, matematyczne, religijne i zupełnie potoczne. Zero to zwykła liczba, zero stopni na termometrze to też temperatura, zerowy stan konta bankowego to przykre, ale spotykane. Odnotujmy, że nie ma w chronologii roku zerowego, a to dlatego, że zero wprowadzone zostało do matematyki dopiero w późnym średniowieczu, później niż zaproponowana przez mnicha Dionizego chronologia (VI wiek).

Dziwne, ale moglibyśmy się naprawdę obyć bez tego zera, a w konsekwencji bez liczb ujemnych. W jednym z podręczników logiki napotkałem ćwiczenie: narysuj albo opowiedz, jak sobie wyobrażasz nieobecność ryby. Niesamowite, prawda? Rybę narysować każdy może, ale jej nieobecność?

Teraz krótki kurs z podstaw matematyki. Przyznanie przywileju istnienia zbiorowi pustemu, oznaczanemu przekreślonym kółkiem ∅, to konieczny zabieg, podobny do dołączania zera do zbioru liczb. Zbiór pusty to jedyny zbiór niezawierający żadnego elementu. Takimi zbiorami są:

• zbiór prostolinijnych okręgów,
• zbiór liczb wymiernych x, takich, że x² = 2,
• zbiór wielorybów mieszkających w Pałacu Kultury w Warszawie.

Ale nie ma dwóch różnych zbiorów pustych. Zbiór pusty jest bowiem zawarty w każdym innym:
dla każdego zbioru X mamy ∅ ⊂ X.
Istotnie, reguły logiki matematycznej mówią, że zbiór A jest zawarty w zbiorze B wtedy i tylko wtedy, gdy zdanie:
x należy do A
pociąga za sobą
x należy do B.

W przypadku zbioru pustego ∅ zdanie x należy do ∅ jest zawsze fałszywe, a więc - na mocy praw logiki - cała implikacja jest prawdziwa. Z fałszu wynika wszystko ("tu mi kaktus wyrośnie, jeśli zdasz do następnej klasy..."). Skoro więc zbiór pusty jest zawarty w każdym innym, to gdyby były dwa różne, każdy z nich byłby zawarty w drugim. Jeżeli jednak dwa zbiory są nawzajem w sobie zawarte, to są równe. Dlatego właśnie: jest tylko jeden zbiór pusty!

Postulat istnienia zbioru pustego nie stoi w sprzeczności z żadnymi prawami matematyki, więc czemu nie powołać go do istnienia? Filozoficzna zasada zwana "brzytwą Ockhama" każe likwidować zbędne pojęcia, ale akurat pojęcie zbioru pustego bardzo się w matematyce przydaje. Odnotujmy, że zbiór pusty ma wymiar -1 (minus jeden) - twory zerowymiarowe to punkty i ich rzadko rozmieszczone układy, twory jednowymiarowe to linie, a o bardzo skomplikowanych tworach matematycznych o ułamkowym wymiarze mówiliśmy w rozdziale o fraktalach.

Interesujące, że cały gmach matematyki: liczby, figury, funkcje, operatory, całki, różniczki, równania, ... może być wyprowadzony z jednego pojęcia - zbioru pustego! Wystarczy założyć, że istnieje zbiór pusty, nowo utworzone elementy można łączyć w zbiory, by móc zbudować calutką matematykę. Oto jak niemiecki logik Gottlob Frege konstruował liczby naturalne. Zero to klasa zbiorów, których elementy są we wzajemnie jednoznacznej odpowiedniości z elementami zbioru pustego. Jeden to klasa zbiorów, których elementy są we wzajemnie jednoznacznej odpowiedniości z elementami zbioru, którego jedynym elementem jest zbiór pusty. Dwa to klasa zbiorów, których elementy są we wzajemnie jednoznacznej odpowiedniości z elementami zbioru złożonego ze zbioru pustego i zbioru, którego jedynym elementem jest zbiór pusty... i tak dalej. Na pierwszy rzut oka wygląda to na coś bardzo skomplikowanego, ale naprawdę nie jest.

Trudne do wyobrażenia

Nicość może być trudna do wyobrażenia. W opowieści Stanisława Lema "Jak ocalał świat" Konstruktor Trurl zbudował maszynę, która miała robić wszystko na literę n. Gdy Klapaucjusz kazał jej zbudować Nic, maszyna zaczęła usuwać ze świata rozmaite przedmioty - z ostatecznym celem usunięcia wszystkiego. "Zrobić Nic, to usunąć wszystko" - wyjaśniła. Zanim przerażony Klapaucjusz zatrzymał maszynę, ze świata zniknęły na dobre kambuzele, ściśnięta, wytrzopki, gryzmaki, rymundy, trzepce, pćmy, graszaki, plukwy, filidrony i zamry. No i rzeczywiście, zniknęły na zawsze…

Bardzo ładnie o nicości pisał Józef Tischner w swojej "Historii filozofii po góralsku". Podczas zeszłych wakacji postanowiłem tej nicości doświadczyć - mianowicie zapuściłem się na torfowiska między Nowym Targiem a Jabłonką na Podhalu. Teren ten nawet nazywa się Pustacią. Idziesz, idziesz, a drogi nie ubywa - oczywiście w naszej skromnej, polskiej skali. Jechałem kiedyś autobusem przez kanadyjską prowincję Saskatchewan. Za oknem rozpościerało się pole kukurydzy. Zdrzemnąłem się na pół godziny. Gdy się obudziłem, jechaliśmy przez to samo pole kukurydzy… Ale, zaraz, czy to jest pustka? W pewnym sensie - brak zmian to właśnie pustka.

Przyzwyczajeni jesteśmy do stałej obecności wokół nas różnych przedmiotów, a od Czegoś nie można uciec nawet zamknąwszy oczy. "Myślę, więc jestem", mówił Kartezjusz. Jeśli już pomyślałem cokolwiek, to znaczy, że Ja jestem, a więc jest na świecie przynajmniej Coś (mianowicie Ja). Czy to, co pomyślałem, istnieje? O tym można dyskutować, ale we współczesnej mechanice kwantowej znana jest zasada Heisenberga: każda obserwacja zakłóca stan obserwowanego przedmiotu. Dopóki nie obserwujemy, to Nic nie istnieje, a gdy zaczynamy patrzeć, obiekt przestaje być Niczym i staje się Czymś. Do granic absurdu doprowadza to zasada antropiczna: nie ma sensu pytać, jaki byłby świat, gdyby nas nie było. Świat jest taki, jaki nam się wydaje. Może inne istoty postrzegałyby Ziemię jako kanciastą?

Pozyton (taki dodatni elektron) jest dziurą w przestrzeni, "brakiem elektronu". W procesie anihilacji elektron wskakuje w ową dziurę i "nic się nie dzieje" - nie ma ani dziury, ani elektronu. Pominę tu liczne dowcipy o dziurach w serze szwajcarskim ("im więcej tego mam, tym mniej mnie jest..."). Znany kompozytor John Cage tak się już wyżyłował z pomysłów, że skomponował (?) utwór muzyczny (?), w którym przez 4 minuty 33 sekundy orkiestra siedzi nieruchomo i oczywiście nic nie gra. "Cztery minuty i trzydzieści trzy sekundy to dwieście siedemdziesiąt trzy, 273, a minus 273 stopni to zero bezwzględne, przy którym każdy ruch ustaje" - wyjaśniał kompozytor (?).

A co ze Wszystkim?

Wielu ludzi (od zwykłych zjadaczy chleba do wybitnych filozofów) zastanawiało się nad fenomenem istnienia. W matematyce sprawa jest prosta: istnieje to, co jest niesprzeczne.

Na drugim biegunie od Niczego leży Wszystko. W matematyce wiadomo, że Wszystko nie istnieje. Jest to po prostu za mało precyzyjne pojęcie, by jego istnienie było wolne od sprzeczności. Można to zrozumieć na przykładzie starego paradoksu: "Jeśli Bóg jest wszechmogący, to czy może stworzyć taki kamień, którego nie może podnieść?" Matematyczny dowód faktu, że nie może istnieć zbiór wszystkich zbiorów, oparty jest na twierdzeniu Cantora-Bernsteina, orzekającym, że "liczba nieskończona" (matematycznie: liczba kardynalna) zbioru wszystkich podzbiorów danego zbioru jest większa od liczby elementów tego zbioru.

Jeżeli zbiór ma n elementów, to jest w nim 2ⁿ podzbiorów; np. gdy n = 3 i zbiór składa się z {1, 2, 3}, to są w nim takie podzbiory:

• trzy zbiory dwuelementowe: w każdym z nich brak jednej z liczb 1, 2, 3,
• jeden zbiór pusty,
• trzy zbiory jednoelementowe,
• cały zbiór {1,2,3}

- razem osiem, 2³, a Czytelnikom, którzy niedawno skończyli szkołę średnią, przypominam stosowny wzór: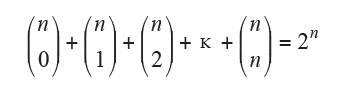

Każdy z występujących w tym wzorze symboli Newtona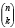określa, ile jest zbiorów k-elementowych w zbiorze n-elementowym.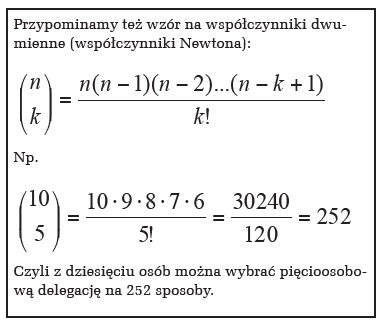

Współczynniki dwumienne występują w matematyce w wielu innych miejscach, np. w interesujących wzorach skróconego mnożenia: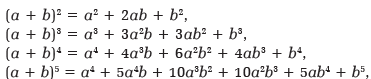

a od ich dokładnej postaci o wiele bardziej interesująca jest ich wzajemna współzależność.

Trudno zrozumieć, że - jeśli chodzi o logikę i matematykę - Nic istnieje, Wszystko zaś nie. Argumenty za nieistnieniem Wszystkiego, są takie same, jak racje Kubusia Puchatka, który zapytał grzecznie swojego gościa, Tygrysa, czy ogólnie rzecz biorąc, Tygrysy lubią miód, żołędzie i oset? "Tygrysy lubią wszystko", odparł ów, z czego Kubuś wydedukował, że skoro lubią wszystko, to znaczy, że lubią też spać na podłodze, ergo, on, Kubuś, może wrócić do łóżeczka.

Inny argument to paradoks Russella. W miasteczku jest fryzjer, który goli wszystkich mężczyzn, którzy nie golą się sami. Czy goli on sam siebie? Obie odpowiedzi są sprzeczne z narzuconym warunkiem, że goli tych i tylko tych, którzy nie robią tego sami.

W poszukiwaniu zbioru wszystkich zbiorów

Na zakończenie przytoczę sprytny, ale jak najbardziej matematyczny dowód tego, że nie istnieje zbiór wszystkich zbiorów (nie mylić z capo del tutti capi).

Najpierw pokażemy, że dla żadnego niepuste - go zbioru X nie da się znaleźć funkcji wzajemnie jednoznacznej, odwzorowującej ten zbiór na zbiór jego podzbiorów, P(X). Przypuśćmy więc, że owa funkcja istnieje. Oznaczmy ją tradycyjnym f. Czym jest f(x)? Jest zbiorem. Czy x należy do f(x)? Nie wiadomo. Albo należy, albo nie. Ale dla pewnego x musi jednak tak być, że nie należy on do f(x). No, to rozpatrzmy zbiór tych wszystkich x, dla których x nie należy do f(x). Oznaczmy go (ten zbiór) przez A. Odpowiada mu pewien element a zbioru X. Czy a należy do A? Przypuśćmy, że należy. Ale przecież A jest zbiorem, który zawiera tylko te elementy x, które nie należą do f(x)… No, to może a nie należy do A? Ale przecież zbiór A zawiera wszystkie elementy o tej własności, więc i a. Koniec dowodu.

Gdyby zatem istniał zbiór wszystkich zbiorów, to sam byłby swoim podzbiorem, co jest niemożliwe na mocy poprzedniego rozumowania.

Uff, nie sądzę, by wielu Czytelnik ów przebrnęło przez ten dowód. Przytoczyłem go raczej po to, by pokazać, czym się musieli zająć matematycy w końcu XIX wieku, kiedy zaczęli badać podstawy własnej nauki. Okazało się, że problemy leżą tam, gdzie się ich nikt nie spodziewał. Co więcej, dla całości matematyki owe spory o podstawy nie mają znaczenia: nieważne, co się dzieje w piwnicach - cały gmach matematyki stoi na mocnej skale.

Tymczasem w najwyższej fazie…

Odnotujmy jeszcze jeden morał, z opowiadań Stanisława Lema. W jednej ze swoich podróży Ijon Tichy dotarł do planety, której mieszkańcy po długiej ewolucji osiągnęli wreszcie Najwyższą Fazę Rozwoju. Są wszechpotężni, wszystko mogą, wszystko mają na wyciągnięcie ręki... i nic nie robią. Leżą na piasku i przesypują go między palcami. "Skoro wszystko można, to nic nie warto" - wyjaśniają zaszokowanemu Ijonowi. Oby tak się nie stało z naszą, europejską cywilizacją…