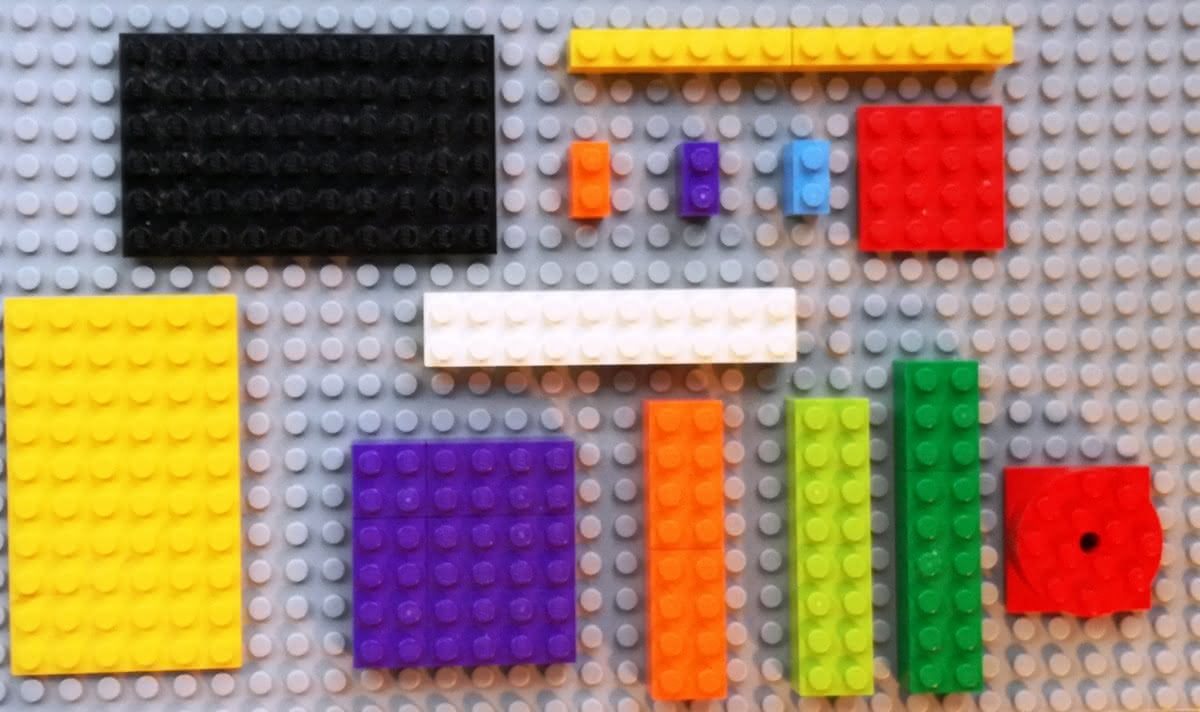Stare klocki, czyli szukając nowych form

Pierwsze koleje na ziemiach polskich zaczęły powstawać przed 1850 r., a w 1875 r. sieć ich była całkiem gęsta. W 25 lat po wynalezieniu radia było ono w dość powszechnym użyciu. Każdy z tych wynalazków zmieniał życie całych społeczeństw. To banalna i ograna prawda.
Po tym przydługim wstępie powiem wreszcie, o co mi chodzi. O szkołę, o nauczanie. Internet i w ogóle komputery zmieniły świat. Musimy zmienić i nauczanie. Nie mam na myśli różnego rodzaju e-learningów. To tylko protezy, to tylko próba wykorzystania nowych technik do staroci, zamontowanie silnika Rolls-Royce’a do wozu drabiniastego. Nie umiem sobie wyobrazić, jak i czego uczyć w przyszłości.
Historia jest nauczycielką życia. Korzystajmy z doświadczeń, próbujmy szukać w przeszłości czegoś, co da się przetransformować do przyszłości.
Co najmniej trzecią część szkolnej nauki geometrii w „moich” czasach zajmowały zadania konstrukcyjne. Młodszym Czytelnikom uzmysłowię: nie chodziło tylko o narysowanie czegoś. Dopuszczalnymi przyrządami były jedynie cyrkiel i linijka, i to nie dlatego, że są to najprostsze i najtańsze przyrządy, i że znane były właściwie już w starożytności: naciągnięta lina to model linii prostej, a narysować łuk koła za pomocą sznurka też łatwo. Zadania konstrukcyjne przyszły do nas z Grecji, przetrwały średniowiecze, Odrodzenie, Oświecenie, kapitalizm XIX wieku… i trzy ćwierci XX wieku. Usunięto je z nauczania właściwie słusznie. Były anachroniczne, no i coś trzeba było usunąć, by pomieścić nowe treści.
Zadania te miały jednak trzy bardzo ważne zalety. Bardzo dobrze uczyły myślenia, w tym myślenia algorytmicznego. Po drugie, dawały pewne ćwiczenia manualne, kształciły sprawność ręki. Po trzecie, były to zadania, w których powstawał konkretny produkt: rysunek właśnie. Produkt nieomal materialny, a nie zaś istniejące tylko w umyśle rozwiązanie jakiegoś równania. W matematyce niewiele jest takich zadań.
Poszukując nowych form nauczania, przypomniałem sobie klocki Lego. Prawdziwe klocki z dzieciństwa… chociaż w zabawie nic nie zastąpi tych najprawdziwszych, drewnianych. Duża rozmaitość rozmiarów, kolorów i kształtów klocków Lego sprawia, że można je wykorzystać od nauczania przedszkolnego do uniwersyteckiego. Mam na myśli klocki typu classic - wyłącznie kostki prostopadłościenne, z charakterystycznymi guziczkami. Budowanie z nich nie tylko jest przyjemne, ale i wpływa na wyobraźnię.
Kolega, któremu to opowiedziałem, zdziwił się nieprzyjemnie: „po co klocki, firma na pewno ma programy na tworzenie dowolnych układanek. Klikasz i masz…”. Zamurowało mnie… ale i przypomniała mi się historia nauczyciela, który w pewnej klasie pokazał dzieciom zjawisko „złamanej łyżeczki” w kubku z wodą. Uczniowie byli zdziwieni i przejęci. W równoległej klasie przeprowadził zaś symulację komputerową - uczniowie przyjęli to obojętnie. Wiadomo, Photoshopem wszystko można.
Ćwiczenie 1 (przedszkole). Pokaż klocki: a) długie, b) krótkie, c) szerokie, d) wąskie, e) małe, f) duże, g) kwadratowe, h) podłużne, i) czarne, j) białe, k) jasne, l) ciemne. Nazwij wszystkie kolory, które widzisz. Które kolory są ciepłe, a które jasne? Autor artykułu jest pod tym względem typowym mężczyzną, dla którego łososiowy, bordo i karminowy to ten sam czerwony, ale z teorii wie, że to co innego i wcale nie uważa, że chłopców należy wychowywać w takiej nieświadomości.
Ćwiczenie 2a (w wersji dla studentów I roku informatyki). W widocznym zbiorze klocków wprowadzamy relację równoważności, uznając klocki za równoważne, jeżeli mają ten sam kolor. Opisz klasy abstrakcji tej relacji. Opisz klasy równoważności relacji, w której za równoważne uznajemy klocki tych samych rozmiarów.
Ćwiczenie 2b (to samo, ale w wersji dla przedszkolaków). Pogrupuj klocki wg kolorów, a potem według rozmiarów. Przejdźmy do szkoły podstawowej, a w każdym razie do materiału, który zrozumieją uczniowie nawet siedmioletni. Najpierw trochę dla dorosłych (nauczycieli). Mamy naturalną skłonność do patrzenia dwubiegunowo. Gdziekolwiek jest przód, jest i tył, gdzie jest lewo, jest i prawo, góra idzie w parze z dołem, prawda z fałszem, południe z północą, wschód z zachodem. Czymże byłby Raj bez perspektywy Piekła? Gdyby nie było plusa, to i minus byłby niepotrzebny. Hет худа без добра. Keine Rose ohne Dornen. Whenever you gain, you lose. Dr Jekyll ma swego Mr Hyde’a, a Batman swojego Jokera. Każdy, kto uczył się języka obcego, zaliczył odpowiednie ćwiczenie: określ antonim danego słowa, np. pełny-pusty, gruby-chudy, szeroki-wąski. To znany z logiki podział dychotomiczny, najprostsza klasyfikacja pojęć i rzeczy: na dwie klasy.
Ćwiczenie 3. Na fot. 1 pokaż, jakie klocki ustawiłbyś w pary. Dlaczego chcesz właśnie tak? Ćwiczenie 4. Czy byłeś może w Pieninach, zwiedzałeś Czerwony Klasztor, płynąłeś Dunajcem, widziałeś Trzy Korony? Ja byłem… i ułożyłem taki obrazek (2). Nie mam zdolności plastycznych - ułóż lepszy. Ale czy na moim obrazku widzisz Czerwony Klasztor (to ten czerwony domek), biały (bo wapienny) szczyt o nazwie Trzy Korony, zielone pola, ciemne góry, żółte słońce i fioletową kładkę nad Dunajcem na słowacką stronę? Na pewno widzisz.
Ćwiczenie 4. Czy byłeś może w Pieninach, zwiedzałeś Czerwony Klasztor, płynąłeś Dunajcem, widziałeś Trzy Korony? Ja byłem… i ułożyłem taki obrazek (2). Nie mam zdolności plastycznych – ułóż lepszy. Ale czy na moim obrazku widzisz Czerwony Klasztor (to ten czerwony domek), biały (bo wapienny) szczyt o nazwie Trzy Korony, zielone pola, ciemne góry, żółte słońce i fioletową kładkę nad Dunajcem na słowacką stronę? Na pewno widzisz.
Gdzie tu jest jakaś matematyka? Spójrz na Dunajec. Czy widzisz, że wszystko się w nim odbija? Górna połówka obrazka jest „taka sama” jak dolna. A właściwie nie taka sama, tylko… no właśnie, symetryczna. Matematycy nazywają to symetrią lustrzaną albo osiową. Wszystko odbite jak w lustrze.
A czy strzała na fot. 3 jest symetryczna? To zależy oczywiście, czy będziemy zwracać uwagę na kolory, czy nie. Matematycy powiedzieliby: abstrahujemy od kolorów, czy nie? Abstrakcja to wyodrębnienie z zespołu cech danego obiektu cechy jednej, interesującej nas. Pan Kowalski będzie zwracać uwagą na markę samochodu, pani Kowalska na kolor. Gdzie jest przód, a gdzie tył figury na fot. 3? Nie mamy wątpliwości – strzała leci „do góry”, światełko czerwone ma z lewej, zielone z prawej. Tak jest w ruchu lotniczym, co teoretycznie znaczy „wyprzedzaj z prawej”. Teoretycznie, bo przecież samoloty nie ścigają się jak samochody. A przy okazji zauważmy, że ten naturalny dla nas kierunek, który pokazuje strzałka, byłby zrozumiały tylko dla cywilizacji, w której kiedyś strzelało się z łuku! Trudno zresztą wypowiadać jakieś ogólne twierdzenia, bo innej cywilizacji przecież nie znamy.
Uczę studentów informatyki. Mają oni trudności z matematycznym wyrażeniem równoległości i prostopadłości. W tym roku potraktowałem ich ilustracjami takimi, jak fot. 4 i 5.
Fot. 4 i 5 dają też piękny przykład abstrakcji. Ani niebieskie, ani żółte, ani zielone klocki na tych fotografiach nie tworzą linii prostej. A jednak „widzimy” tam te linie. Umiemy je sobie wyabstrahować z rysunku. Klocki Lego dobrze uczą kreatywności.
Ćwiczenie 5. Czy zieloną „serwetkę” na fot. 6 da się ułożyć z klocków o wymiarach 4 x 2? Mając do dyspozycji klocki aż do rozmiaru 2 x 8, ułóż tę „serwetkę” z jak najmniejszej ich liczby.
Ćwiczenie 6 (dla licealistów). Oblicz pole serwetki o n ząbkach. Na fot. 6 widzisz serwetkę o ośmiu ząbkach.
Rozwiązanie. Dopełnijmy tę figurę do pełnego kwadratu za pomocą trójkątów, z których jeden jest widoczny na fot. 7. Jeżeli jest n rożków na jednym boku, to każdy z trójkątów dopełniających ma następujące pole: najpierw 6, a potem suma ciągu arytmetycznego o n-2 wyrazach (z których początkowy to 8) i różnicy 6. Jest to równe 3n2-13n+26. Kwadrat ma bok 4n+2, łączne pole figury jest równe (4n+2)2 – 4(3n2-13n+26) = 4(n2+17n-25).
Ćwiczenie 7. Oblicz pola takiej „serwetki” (8)
Zadanie. Jaki wzór skróconego mnożenia widzisz na fot. 9?