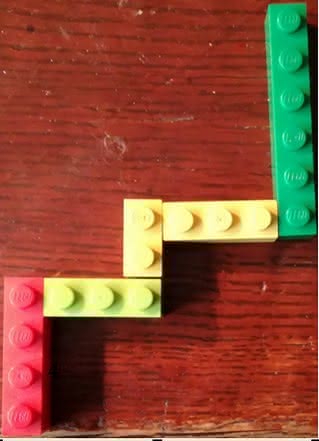Uroki spirali Archimedesa

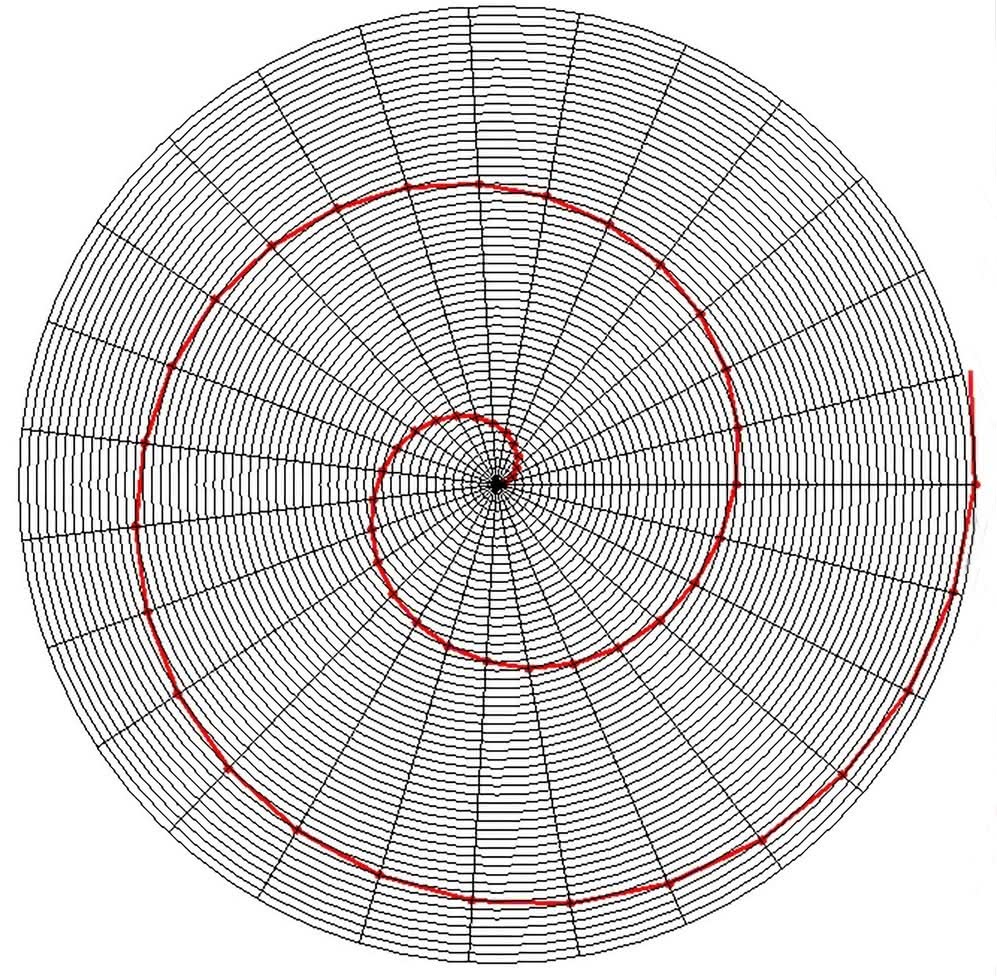
Rowki na tego rodzaju płycie są ułożone w spiral ę Archimedesa. Taka krzywa charakteryzuje się stałym odstępem między kolejnymi zwojami. Jej równaniem we współrzędnych biegunowych jest

r = aφ,

gdzie a to pewna stała dodatnia, φ – kąt, zaś r – promień wodzący. Można powiedzieć, że promień rośnie proporcjonalnie do kąta. Jeszcze prościej – po spirali Archimedesa będzie poruszać się mucha, drepcząca wzdłuż promienia obracającej się płyty. Widzimy to na ilustr. 1, a jeszcze lepiej na ilustr. 2 – czerwona linia łamana łączy kolejne węzły siatki. Sama spirala jest krzywą ciągłą, powstającą przez kolejne przybliżenia łamanymi.

2. Spirala Archimedesa - krzywa ciągła, powstająca przez kolejne przybliżenia łamanymi

Spirale mogą być lewo- albo prawoskrętne. Ich wzajemne przenikanie się daje ładny obrazek (3). Na ilustr. 4 mamy zaś kilka spiral o wspólnym wierzchołku (tzn. o różnych parametrach a).

3. To nie jest przekrój tuneli metra… - to tylko fragmenty dwóch spiral

Ciekawa jest układanka z klocków Lego (5) - moglibyśmy widoczny tam deseń nazwać „czworokątną spiralą Archimedesa”; tak jakby na ilustr. 1 pokazać nie siedem ramion, a cztery.

4. Różne lewoskrętne spirale Archimedesa - przypomina to załamującą się falę morską

Zadanie 1. Czy potrafi my obliczyć długość takiej spirali? Jednostką są „guziczki” klocków.

Spróbujmy. Pierwszy zwój (biały) zawiera 11 „guziczków”, następny, pomarańczowy, ma 5+6+7+8=26. Każdy bok ma długość o 1 większą. Ostatni ma długość 47. Mamy zatem do obliczenia sumę S=11+5+6+7+8+9+10+…+46+47

Możemy to zrobić tzw. sposobem Gaussa. Najpierw napiszmy tak:

S=1+1+2+3+4+5+….+46+47

Obliczmy teraz

2·S=2+2·(1+2+3+4+5+….+46+47)= =2+2·((1+47)+(2+46)+(3+45)+(23+25)+(24+24))= =2+2·24·48=2306

To jest wartość podwojonej sumy „guziczków” na klockach, a zatem S=1153. Można to zresztą obliczyć standardową metodą szkolną, podstawiając do wzoru na sumę ciągu arytmetycznego.

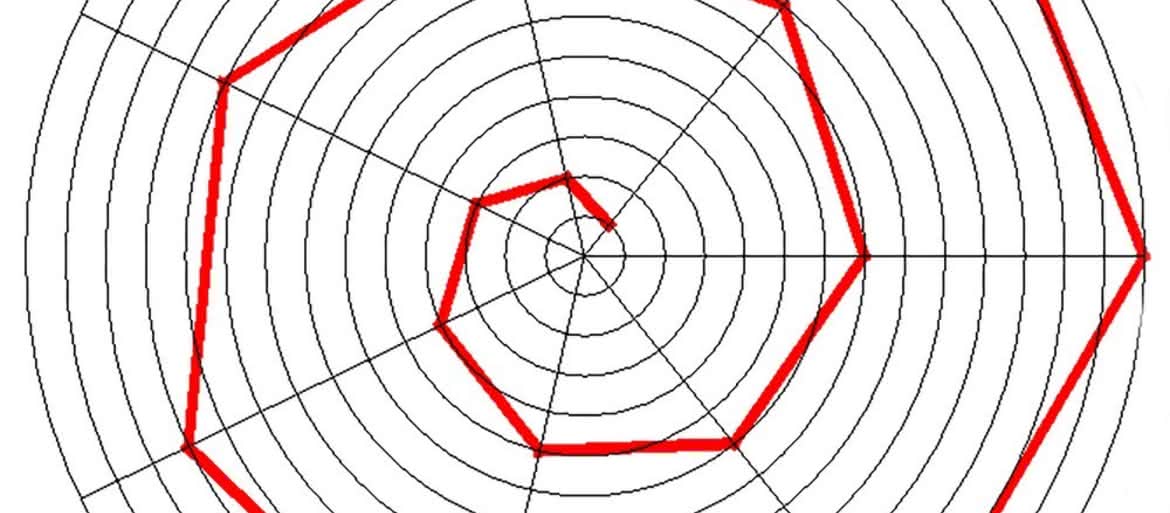
Zadanie 2. W którym miejscu „spirali” widocznej na ilustr. 5 znajdzie się liczba 2017?

Zadanie 3. Jakie liczby stoją w narożnikach „spirali” z ilustr. 5 - tzn. tam, gdzie zmienia ona swój kierunek? Odkryj ogólny wzór opisujący te liczby.

Zadanie 4. Spójrz teraz na ilustr. 6. Czy widzisz tam dwie spirale? Jedna z nich składa się z zielonych klocków, druga z na przemian pomarańczowych i fioletowych. Jaka jest długość kolejnych klocków pomarańczowych? Jaka jest długość kolejnych klocków fioletowych? To jest zadanie bardziej na spostrzegawczość niż z arytmetyki…

5. „Czworokątna spirala Archimedesa” ułożona z klocków Lego

6. Dwie spirale: jedna zielona, druga pomarańczowo-fioletowa

Zadanie 5. Długość zielonej spirali na ilustr. 6 wynosi 66 (za jednostkę długości bierzemy teraz dwa guziczki – bok kwadratowej płytki, z której jesteśmy w stanie ułożyć wszystko). Można to policzyć. Da się obliczyć „sprytnie”, tak jak długość spirali na ilustr. 5 (zadanie 3). Można jeszcze łatwiej. Ile jest klocków fioletowych (tzn. nie tyle klocków, co kwadracików 2×2)? Po jednej stronie 2+6+10, po drugiej 4+8+12, co daje razem 42. Klocków (kwadracików) pomarańczowych jest 36. Razem 78. Wszystkie klocki (trzech kolorów) wypełniają kwadrat 12 na 12. Zielonych klocków jest zatem 144–78=66. Zgadza się! Wyobraź sobie, że spirale (dwie!) jak na ilustr. 6 układam dalej. Wyprowadź ogólny wzór na długość obu spiral („pomarańczowo- fioletowej” i „zielonej”) o n odcinkach. Czym się różnią te dwie spirale?

Zadanie 6. W zestawie klocków Lego dla pierwszej klasy szkoły podstawowej jest takie zadanie: ułożyć węża z klocków. Algorytm układania możemy zapisać w postaci ciągu liczb, np. (4, 3, –2, 4, –5). Interpretujemy to tak: połóż najpierw klocek długości 4 (kierunek obojętny, a zamiast klocka długości 4 może być cztery razy po 1, 2 plus 2, 1 plus 3 i 3 plus 1), następnie skręć w prawo i idź trzy jednostki, potem w lewo 2, w prawo 4 i w lewo 5 - kierunek skrętu poznajesz po znaku liczby. Otrzymasz „węża” z ilustr. 7. Przemyśl, dlaczego ostatnie dwie liczby w tej notacji są 4, –5, chociaż ostatni klocek ma długość 6 - „powinno być” zatem –6.

7. Wąż (4, 3, –2, 4, –5)

Spirala Archimedesa nadaje się doskonale do zilustrowania prostego twierdzenia, które udowodnił w 1981 r. Karol Borsuk, nieco zapomniany dzisiaj jeden z wielkich polskich matematyków lat 1930-1980. Karierę jego przerwała oczywiście wojna - jak całe pokolenie stracił na niej najlepszy okres swojego nie tak bardzo długiego życia (1905-1982). Spójrzmy na spiralę. Gdybyśmy na niej mieszkali i gdyby nie było otaczającej przestrzeni, żyłoby się tak, jak na linii prostej. Krzywizna stawałaby się niezauważalna – jest bowiem pojęciem z „wyższego wymiaru”. Linie i powierzchnie są zakrzywione w pewnej większej przestrzeni – dlatego tak trudno nam zrozumieć, że nasza trójwymiarowa, otaczająca nas przestrzeń, jest zakrzywiona w czasoprzestrzeni. Dokładniej: być może jest zakrzywiona w niej.

Karol Borsuk wykazał, że przestrzeń euklidesowa może być zanurzona w kulę o dowolnie małym promieniu w przestrzeni wymiaru większego o 1. Nie ma tu miejsca na dokładne omówienie tego sposobu, ale spójrzmy jeszcze raz na spiralę (czyli przypadek n=1). Dla jej mieszkańców nie ma możliwości dostania się z jednego zwoju na drugi inaczej niż po prostu idąc po linii. Natomiast „UFO-ludki”, istoty nie z tej przestrzeni, mogą przeskoczyć z jednego zwoju na drugi przez przestrzeń i wyprzedzić nawet światło, podróżujące w naszej przestrzeni, czyli po zwojach spirali. To spowoduje u nas, mieszkańców spirali, wrażenie podróży w czasie. Oczywiście sam Karol Borsuk się z tego śmiał, ale dziennikarze mieli przez pewien czas trudność w zrozumieniu, czy to tylko żart, czy rzeczywiście polski uczony wyjaśnił tajemnicę podróży w czasie.

Kilka lat temu zdobyła pewną popularność gra planszowa w zwierzątka - grający prowadził farmę, celem było zdobycie maksymalnego zysku. Grę tę wymyślił właśnie Karol Borsuk, w czasie wojny, dla zarobku. Po wielu latach ktoś sobie o niej przypomniał.

***

Odejdę na chwilę daleko od tego, o czym piszę i o czym tylko chciałbym pisać. Zauważam z przerażeniem, że jest coraz więcej osób, gloryfikujących czas wojny i coraz więcej gier wojennych dla młodzieży, coraz więcej zabawy w wojnę. Moje pokolenie wzrastało na ruinach Warszawy i wojnę znam tylko z opowieści. Niech tak zostanie, a militaryści niech wyżyją się np. na robotach drogowych...

***

8. Zamiana ruchu obrotowego na postępowy

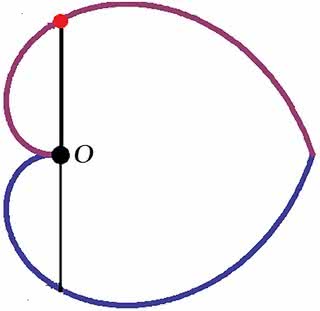
Spirala Archimedesa ma zastosowanie w mechanizmach, gdzie potrzebna jest zamiana ruchu obrotowego na postępowy – lub odwrotnie. Przy obrocie wokół punktu O spirala „wpycha” zaznaczony punkt czerwony w odcinek do środka O i potem dalej poza ten punkt. Żeby zrozumieć, że otrzymujemy ruch jednostajny, wystarczy przypomnieć sobie sytuację, od której zaczęliśmy – mucha pełznie jednostajnie po obracającej się płycie. Przestrzenną odmianę tej krzywej wykorzystał Archimedes do konstrukcji pompy wodnej. Może jego wynalazek spowodował polepszenie losu kilku niewolników – zamiast noszenia wody w metalowych wiadrach, niewolnik taki przekręcał tylko wyłącznik pompy i elektryczność wykonywała pracę. Rzut oka na zegarek i: „Jak to dobrze, że jest pompa. Zdążę do domu tramwajem na transmisję z Igrzysk Olimpijskich… O jedzenie nie muszę się martwić – mój pan właśnie ofiarował bogom sto wołów jako ofiarę z okazji odkrycia ważnego twierdzenia, a zatem będzie dużo hamburgerów...”

Często myślę, jak starożytni Grecy byli w stanie odkryć tak wiele matematyki nie tylko bez komputera, ale papieru i ołówka! Ale to inny temat.