Refleksje przy liczbach trójkątnych

Mam w swoim księgozbiorze (dla młodych Czytelników: zajrzyjcie do Internetu, co znaczy to słowo; kiedyś wiedzę zdobywało się z czytania tzw. książek) broszurkę Wacława Sierpińskiego o liczbach trójkątnych. Stoi tak sobie od ponad pięćdziesięciu lat… Tak, tak, niektórzy ludzie tak długo żyją. Wydały ją Państwowe Zakłady Wydawnictw Szkolnych (obecnie WSiP, Wydawnictwa Szkolne i Pedagogiczne), w serii Biblioteczka Matematyczna. Miałem również (ale gdzieś się zapodziało przy kolejnych przeprowadzkach) wydanie z 1948 r., czyli sprzed lat blisko siedemdziesięciu.
Co to są liczby trójkątne? Rzut oka na ilustrację 2 wyjaśnia wszystko. Ile kulek potrzeba, by utworzył się „równy” trójkąt? Wiemy wszyscy, że matematycy mówią na niego: równoboczny. Może na wszelki wypadek przypomnę: trójkąt równoboczny jest też równoramienny, ale nie każdy równoramienny jest równoboczny. A więc kolejno mamy 1, 3, 6, 10, 15, 21, 28, 36, 45, …. kulek, a dokładniej, jak widzimy, cukierków.
Zrobiłem to zdjęcie w trakcie zajęć z klockami Lego, prowadzonych fachowo przez zespół Lego Education. Nietrudno wyprowadzić ogólny wzór na liczbą trójkątną. To przerabia się w szkole, z okazji ciągu arytmetycznego:
1 + 2 + 3 + … + n = .
Można tę formułę ładnie zilustrować geometrycznie. Wybiorę inną metodę. Niech liga piłkarska ma n drużyn. Na koniec sezonu ustala się tabela. Policzmy, ile meczów trzeba było rozegrać. Pierwsza drużyna grała z każdą z pozostałych n-1, druga n-2… itd. Łącznie daje to 1+ 2 + … + n meczów. Ale każda drużyna grała z każdą po jednym razie, a zatem meczów było właśnie .
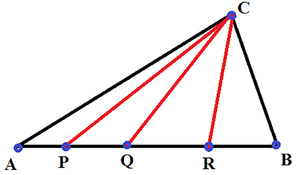
Do liczb trójkątnych dochodzimy w bardzo wielu sytuacjach. Ile trójkątów jest na ilustracji 3? Cztery? Nie. Dziesięć. Oto one:
ABC, ARC, AQC, PBC, QBC, RBC, PRC, QRC, PQC, APC
Gdy z wierzchołka C poprowadzimy n prostych, dostaniemy właśnie Tn trójkątów.
Trójkąt jest najprostszą figurą płaską, można go zrobić z trzech patyczków. Czworościan ma sześć krawędzi. Jest bryłą sztywną – połączone nawet przegubowo druciki nie dadzą się zdeformować. Wielowymiarowy odpowiednik tych figur nazywa się sympleksem. Wśród nich jest sympleks foremny. Gdy n = 2, dostajemy dobrze znany trójkąt równoboczny, a dla n = 3, otrzymujemy czworościan foremny.
Jaką bryłą jest sympleks foremny czterowymiarowy?
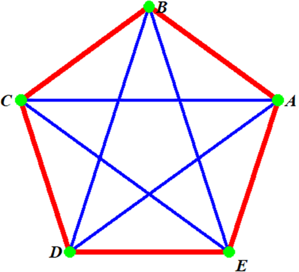
Jest on utworzony przez pięć punktów połączonych odcinkami tak, by każdy miał taką samą długość. W przestrzeni czterowymiarowej da się to zrobić, w trójwymiarowej nie! Dwuwymiarowy rysunek (a przecież innych nie umiemy robić) wygląda tak:
Jest to też graf zupełny o pięciu wierzchołkach. Jeśli w eliminacjach mistrzostw świata występuje pięć drużyn, to każda gra z każdą – a jeśli zaplanowano mecz i rewanż, to jest on jeszcze skierowany. Łączymy kilka, kilkanaście, kilkadziesiąt, ... , wierzchołków, każdy z każdym. Za każdym razem dostajemy liczbę trójkątną.
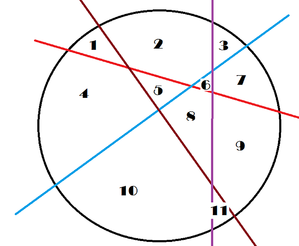
Pisałem wyżej o „wspomnieniach z młodości”. Otóż tylko raz mama pozwoliła mi pokroić tort urodzinowy. Obiecałem, że zrobię to starannie i jak najprościej. Wziąłem nóż, umoczyłem w gorącej wodzie (lepiej się kroi) i… ignorując wszelkie zasady, poprowadziłem, jak młodemu matematykowi przystało, kilka płaskich cięć jak na ilustracji 5. „To najprostszy sposób podziału na jedenaście części – wymaga tylko czterech cięć, a goście na pewno docenią matematykę zawartą w tym podziale” argumentowałem, ale mama była głucha na tę przecież nieubłaganą logikę. A dla Czytelników mam takie zadanie: co to ma wspólnego z liczbami trójkątnymi?
Dygresje, czyli komu kłaniać się w pas
Oto kolejne ładne zadanie:
Zadanie. Niech m oraz n będą kolejnymi liczbami trójkątnymi. W pojemniku jest m kulek czerwonych i n kulek niebieskich (6). Losujemy bez zwracania dwie kulki. Wtedy prawdopodobieństwo, że wylosujemy dwie kulki różnych kolorów wynosi 50%. Inaczej mówiąc: prawdopodobieństwo wylosowania dwóch czerwonych lub dwóch niebieskich jest także równe 50%.
Nie siląc się na ogólny dowód, zobaczmy przypadek, gdy m = 6, n = 10
Losujemy pierwszą kulkę. Szansa, że jest ona niebieska, wynosi 6 do 16. Zostaje piętnaście kulek, w tym pięć niebieskich. Nadchodzi drugie losowanie. Jakie są nasze szanse na niebieską kulkę? 5 do 15, czyli jedna trzecia. Ułamki te trzeba pomnożyć, a wynikiem jest jedna ósma. Mamy jedną szansę na osiem, że wylosujemy dwie niebieskie.
Z czerwonymi jest zupełnie inaczej. Za pierwszym razem szanse na czerwoną to 10 do 16, za drugim – 9 do 15. Iloczyn tych ułamków to trzy ósme. Łącznie szanse na jednokolorowy wynik dwóch losowań to jedna trzecia plus trzy ósme, czyli jedna druga.
I tu rozbudowana dygresja. Zaprezentowałem to rozwiązanie swojemu koledze, specjaliście od zadań maturalnych. „Dwa punkty na pięć możliwych”, powiedział. Zdziwiłem się – metoda jest dobra, wynik poprawny, dlaczego nie postawiłby mi maksymalnej liczby punktów? „Jak to dlaczego?”, zdziwił się z kolei on. A gdzie Omega?
Teraz ja sobie z kolei przypomniałem, że w zadaniach z rachunku prawdopodobieństwa owa Omega jest bożkiem. Należy się jej kłaniać w pas. Młodsi i starsi Czytelnicy pamiętają: trzeba najpierw określić zbiór zdarzeń elementarnych – czyli jakie wyniki będziemy badać. U nas Omega składa się aż z 240 elementów, trzeba je wyszczególnić. Są to wyniki dwóch losowań – pierwsze z szesnastu kulek, drugie z piętnastu. Daje to 240 możliwości i z tego należy pracowicie wybrać „sprzyjające”. Owszem, jest ich 120.
Skąd to się wzięło? Rachunek prawdopodobieństwa został dołożony do programów szkolnych na fali reform: przedłużenia czasu nauki z jedenastu do dwunastu lat i swoistej mody na matematykę. To, czego uczyli się ówcześni uczniowie, dziś poznają dopiero studenci i to często nie pierwszych lat – a całe obszary np. geometrii w ogóle wyrzucono. Rachunek prawdopodobieństwa miał być nauczany lege artis, z nabożeństwem należnym dyscyplinie matematycznej: miały być aksjomaty i przestrzeń probabilistyczna.
W jednym z opowiadań Stanisława Lema pilot Pirx ląduje na planecie, która jest do metra wysokości napełniona wodą. Okazało się, że dawniej planetę trapiła potworna susza. Odpowiednie służby zabrały się do jej zwalczenia. Powstały biura, urzędy i instytucje zajmujące się tylko nawodnieniem planety. Niestety, nie zauważono, kiedy planeta była już wystarczająco nawodniona – i działali dalej. Tak jest właśnie z nauczaniem rachunku prawdopodobieństwa. Uczniowie mieli poznać gruntownie pewną teorię matematyczną – od aksjomatów do pięknych twierdzeń, mających ponadto zastosowanie w życiu. Co z tego zostało? Zbiór zadań służących tylko temu, żeby było co zdawać na maturze.
Tu koniec pierwszej dygresji. A druga dotyczy mojego „hobby” wewnątrzmatematycznego. Zadania, jakie dajemy uczniom, nie zmieniły swojego charakteru od kilku pokoleń. A ja chcę inaczej. Jak? Ano, np. zamiast zadania takiego:
Zadanie. Niech m oraz n będą kolejnymi liczbami trójkątnymi. W pojemniku jest m kulek czerwonych i n kulek niebieskich. Losujemy bez zwracania dwie kulki. Uzasadnij, że prawdopodobieństwo, iż wylosujemy dwie kulki różnych kolorów wynosi ½. Inaczej mówiąc: prawdopodobieństwo wylosowania dwóch czerwonych lub dwóch niebieskich wynosi także ½.
dajemy zadanie odwrotne:
Zadanie. W pojemniku jest m kulek czerwonych i n kulek niebieskich. Losujemy bez zwracania dwie kulki. Wiemy, że prawdopodobieństwo, iż wylosujemy dwie kulki różnych kolorów wynosi ½. Inaczej mówiąc: prawdopodobieństwo wylosowania dwóch czerwonych lub dwóch niebieskich wynosi także ½. Jaka jest proporcja m do n?
Co za różnica? Zasadnicza. Pierwsze jest na podstawienie do wzoru, drugie – na myślenie. Wszyscy głoszą, że szkoła ma uczyć myślenia. I właśnie tego nie uczymy. Dlaczego? Bo zadania sztampowe łatwiej sprawdzać.
To koniec drugiej dygresji.
Co przyciąga dziś słuchaczy?
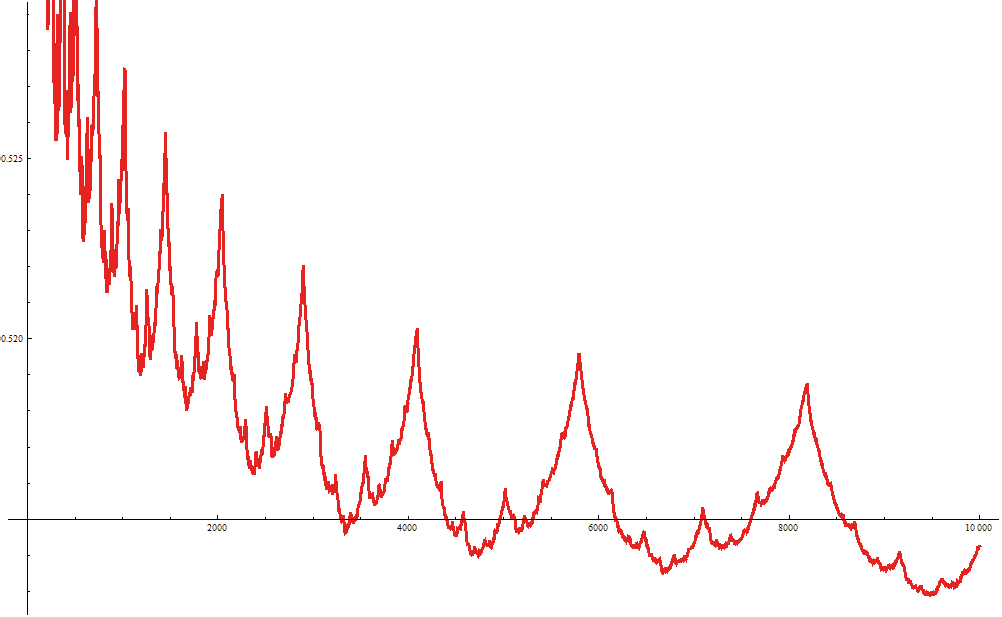
Wykres na ilustracji 7 przypomina jakąś krzywą fraktalną. Kolejne garbki nie są jednak ściśle podobne. Zmieniają nieco kształt. Takie krzywe rozpatrywał twórca teorii fraktali, Benoit Mandelbrot (1924-2010) w swojej ostatniej pracy matematycznej, gdzie próbował zastosować takie właśnie ogólniejsze fraktale do opisu zjawisk giełdowych. Ale wykres, który widzimy, nie jest giełdowy. Zrobiony został tak oto:
Przedstawiamy kolejne liczby trójkątne w postaci dwójkowej: 3 = 112, 6 = 1102, 10 = 10102, 15 = 11112, i tak dalej. Dla każdej liczby trójkątnej obliczamy następnie proporcję jedynek w jej rozwinięciu dwójkowym, a wykres pokazuje wyniki zbiorcze. Zgodnie z oczekiwaniami, udział jedynek dąży do jednej drugiej – to znaczy, że bardzo duże liczby mają w przybliżeniu tyle samo zer i jedynek.
Wacław Sierpiński (1882-1969) był jednym z najsławniejszych polskich matematyków. Z Benoit Mandelbotem łączy go miejsce urodzenia (Warszawa) i… fraktale. Tzw. dywan Sierpińskiego był pierwszym fraktalem, badanym przez matematyków.
Sierpiński zasłynął najbardziej w teorii liczb. Pamiętam jeszcze jego wykłady – prowadzone wbrew wszelkim zasadom dydaktyki. Mówił cicho, do tablicy, nadużywał zwrotu „jak to państwo możecie przeczytać w moich książkach”, nie zwracał uwagi na audytorium – a jednak przyciągał słuchaczy, być może swoją reputacją. Słuchacze też byli zresztą inni niż dzisiaj.
No i właśnie. O tym chciałem na koniec trochę napisać. Wiosną tego roku miałem zajęcia dla studentów sekcji pedagogicznej pewnego uniwersytetu. Pokazywałem m.in. ciekawostki związane z liczbami trójkątnymi. Próbowaliśmy np. ilustrować zależności między nimi za pomocą klocków Lego, o których wiele pisałem w poprzednich miesiącach. Spójrzmy na ilustrację 8. Widzimy tam ciekawe zależności, dwie spośród niezliczonej liczby związków między liczbami trójkątnymi. Próbowałem tym zainteresować owych studentów. Teoria liczb jest nazywana „królową matematyki” i jest w tym wiele racji, ale o tym nie tym razem. Reakcja ich była jednoznaczna: „Po co nam się tym zajmować, tego nie będzie na żadnym egzaminie…”. Na zadaną pracę domową – „ułóżcie z klocków Lego inne zależności między liczbami trójkątnymi” – stworzyli… boisko piłkarskie, dając tym dowód, że są na poziomie mniej więcej dwunastolatków. Internet, smartfony, I-pady, e-learning, platformy moodle, cała niesamowita technika informatyczna rozwinięta w XXI wieku, na naszych oczach, sprawia, że bez telefonu w ręku czują się jak moje pokolenie bez butów na wiejskiej drodze (a moja babcia, prosta kobieta z podlubelskiej wsi, chodziła całe lato boso) – intelektualnie pozostają cofnięci o kilka lat w porównaniu z pokoleniem ich rodziców.
Te moje gorzkie słowa nie są wynikiem tylko jednostkowego zdarzenia, a kilkunastoletniej obserwacji studentów nienależących do ścisłej elity kraju – bo ci z kolei znajdują się na niewyobrażalnie wysokim poziomie. Może tak musi być, może musi istnieć tak olbrzymia rozpiętość… Proszę nie zapominać, że jestem dzieckiem PRL-u i dałbym się posiekać za obronę poglądu, że nie wszystko było tam złe. Oczywiście wiem, że największą zaletę ówczesnego ustroju stanowiło to, że byłem w nim młody…
No dobrze, już kończę. O liczbach trójkątnych mógłbym napisać np. w następnym odcinku, ale P.T. Czytelniku: Google, Wikipedia i Wolfram nauczą Cię więcej niż ja tutaj.
Miłej lektury.