Basia bawi się klockami

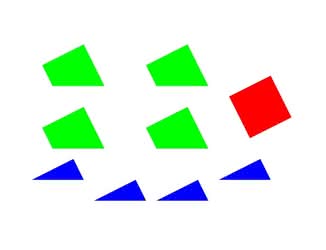
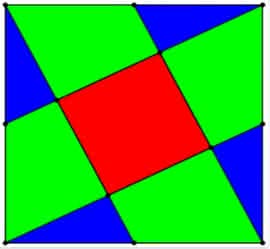
– Basiu, masz już sześć latek i wiesz, co to jest kwadrat. Pokaż, który klocek na rys. 1 jest kwadratowy. Bardzo dobrze. Ten czerwony. A ile masz klocków trójkątnych? Brawo, cztery niebieskie to trójkątne. Nauczę cię teraz nowego słowa. Klocki to trapez. Ile jest razem klocków: cztery niebieskie trójkątne, cztery zielone trapezy i czerwony kwadrat. Czy potrafisz ułożyć duży kwadrat ze wszystkich tych dziewięciu klocków? Mówisz, że to nietrudne. Masz rację (rys. 2). – A teraz powiedz, Basiu, jaką część dużego kwadratu zajmuje mały, czerwony?
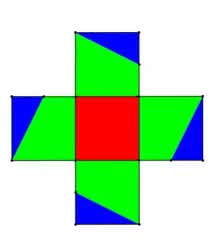
Podpowiem ci, ułożę klocki inaczej. O, tak. Widzisz (rys. 3)?
– Widzę, proszę pana. Basia jest jeszcze malutka, chodzi do przedszkola i nie zna ułamków. Ale kiedy Basia pójdzie do szkoły, to nauczy się, że czerwony kwadrat to jedna piąta dużego. Jedna piąta, . Pan już na pewno zna się na ułamkach? A dobrze?
– Tak, Basiu, dość dobrze. A ułożyłabyś coś ładnego, gdybyś miała więcej takich klocków?
– Tak. Bo my mamy podobne kafelki w łazience. Tylko kolory są inne. Jakie to ładne! Dwa ukośne paski z kwadracików i duże kwadraty, a najładniejsze to takie niebieskie wiatraczki. Wydaje mi się, że to się wszystko kręci.
– Prawda, Basiu? Popatrz: ten wzorek „co pewien czas” się powtarza. W ukośnych rzędach co szósty kwadrat jest pełny, czerwony. Poziomo i pionowo wzorek powtarza się co kwadrat.
– I można nim kręcić. To robią wiatraczki. Czy Basia będzie się uczyć w szkole o tym?
– Nie, Basiu, tak naprawdę to dopiero po szkole.
– To po szkole jest jeszcze coś? Przecież nauczyciele wszystko umieją.
– Basiu! Nie garb się. Spójrz jeszcze na niebieski trójkąt. Czy wiesz, jak on się nazywa?
– Wiem. Niebieski.
– Czy ma coś równego?
– Nie, boki są nierówne.
– A kąty?
– Też nierówne. Aha, czy ma coś prostego? No, tak, kąt prosty. To wiem, że taki równy kąt nazywa się prosty. Bo jest prosty. Równiutki. Ani za duży, ani za mały.
– Basiu, a ten najostrzejszy kąt, tam gdzie dzióbek?
– Proszę pana, już mówiłam. Basia ma sześć latek i nie zna się na trygonometrii. Mój tatuś powiedział, że to dopiero w liceum. Kiedy Basia dorośnie, to pan przyjdzie i spyta, i wtedy Basia mu wytłumaczy, że tangens tego mniejszego kąta jest równy 2, więc sam kąt to w przybliżeniu… a zresztą niech pan sobie sam obliczy, bo Basia nie umie równań trygonometrycznych. A jakby złożyć dwa niebieskie trójkąty w jeden, to powstałby taki ciekawy, w którym wysokość jest równa podstawie. A na razie mam ważniejsze sprawy na głowie. Widzi pan, moja Zuzia, ta moja ulubiona lalka, jej już oczka się zamykają i muszę ją położyć spać.
***
Upłynęło kilka lat, Basia jest już w szkole. Znów pojawia się zadanie z przedszkola, tylko, że się tak wyrażę, w innym setupie.
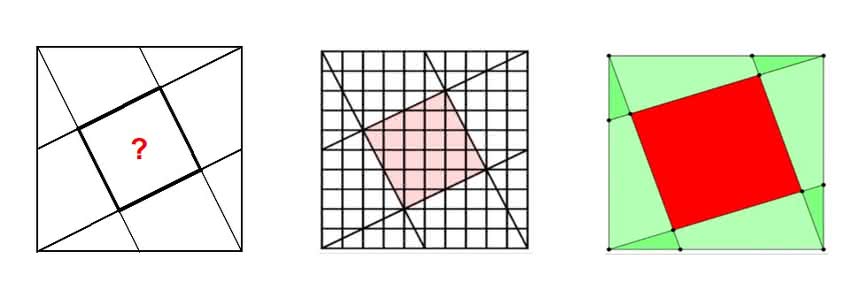
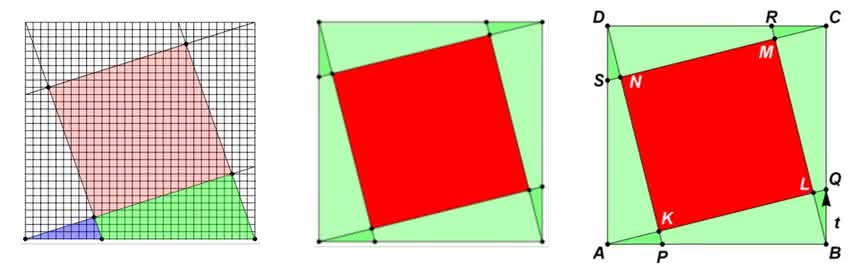
Zadanie 2. Łączymy wierzchołki kwadratu o danym boku, ze środkami odcinków następnych boków. Oblicz pole kwadratu, powstałego wewnątrz (rys. 5).
Nie wiem, czy wpadłbyś szybko na pomysł, żeby zrobić to tak, jak Basia w przedszkolu. Zróbmy inaczej, innym sposobem, też pomysłowym, a bardziej regularnym. Przyda się potem. Narysuj na kratkowanym papierze; duży kwadrat ma mieć rozmiary 10 na 10 kratek (jak w grze w okręty). Wszystko możesz teraz łatwo poobliczać (rys. 6)!
O właśnie. Sposób Basi nie przyda się, gdy zadanie będzie nieco inne.
Zadanie 3. Łączmy wierzchołki kwadratu z punktami znajdującymi się w jednej trzeciej przeciwległych boków, tak jak na rys. 7. Oblicz pole kwadratu wewnątrz.
Tym razem podpowiedź nic nie da. Zobaczyłbyś wszystko, ale przy podziale kwadratu na 340 razy 340 części. To za dużo rysowania. No dobrze, ale skąd ja to wiem? Wiem, bo rozwiązałem zadanie ogólniejsze. Tak bywa, że łatwiej jest rozwiązać zadanie ogólniejsze.
Podpowiem ci. Zrób większy rysunek, w kwadracie 30 na 30. Rysuj starannie, a wszystko zobaczysz (rys. 8).
Możesz już obliczyć, co trzeba. Ale zadanie matematyczne tym się różni od łamigłówki, że chcemy je rozwiązać w możliwie pełnej ogólności. Co będzie, gdy na bokach weźmiemy punkty, powiedzmy, w jednej czwartej długości? Spójrzmy na rys. 9.
Tym razem podpowiedź nic nie da. Zobaczyłbyś wszystko, ale przy podziale kwadratu na 340 razy 340 części. To za dużo rysowania. No dobrze, ale skąd ja to wiem? Wiem, bo rozwiązałem zadanie ogólniejsze. Tak bywa, że łatwiej jest rozwiązać zadanie ogólniejsze.
Nie będę dzielił boku na n części, tylko wprowadzę parametr t. Będzie nim czas, dlatego wziąłem oznaczenie t. Po łacinie „czas” to tempus, stąd pochodzi angielskie time i francuskie temps. Jeżeli nie wiesz, co znaczy słowo „parametr”, nie przejmuj się, zrozumiesz zaraz. Wyobrażam sobie, że punkt Q dźwiga się do góry po odcinku BC, a wszystkie inne poruszają zgodnie z nim – zostawiając wewnątrz malejący kwadrat czerwony. Czas biegnie od zera do 1, w umownych jednostkach. Rys. 10 jest jakby fotografią sytuacji w pewnym momencie czasu.
I teraz patrz na zielone trójkąty. Są w różnych odcieniach zielonego, specjalnie. Analizujmy tylko dolne: AKP, ABQ, ALB. Są to trójkąty prostokątne. Mają wspólny kąt A. Ich boki są więc proporcjonalne. Ale i bez skomplikowanej geometrii można znaleźć stosowną zależność. Niech po odcinku AQ pełznie do góry robaczek. Ma on pod górkę, ale nachylenie górki nie zmienia się. Nie jest ani mniej pochyło, ani więcej. To znaczy, że nachylenie w punkcie Q do podstawy AB jest takie samo, jak przy P. Inaczej mówiąc:
BQ/BC = AK/KP
Ale BQ/BC = t. Mamy stąd AK = t·KP . Jednocześnie AK2 + KP2 = AP2. Znajdujemy stąd długości:
AK = t2/√t2 + 1 , KP = t/√t2 + 1 .
Możemy obliczyć długość odcinka AQ. Zastosujemy twierdzenie Pitagorasa do trójkąta prostokątnego ABQ. Mamy:
AQ = √ AB2 + BQ2 = √ 1 + t2
I dzięki temu możemy łatwo obliczyć długość boku kwadratu KLMN. Przecież
AQ = AK + KL + LQ = AK + KL + KP,
Ostatecznie:
KL = √ 1 + t2 - t2/ √ 1 + t2 - t/ √ 1 + t2= 1 - t / √1 + t2.
Zwrócę ci uwagę na ważną sprawę – nie tylko w rozwiązywaniu zadań matematycznych, ale wszędzie. Jeśli to możliwe, zawsze sprawdź, czy rozwiązanie jest dobre; najlepiej inną metodą. Ja sprawdzę to tak. Podstawię t = 1/2 Co wyjdzie? A co ma wyjść? Jedna piąta. Dlaczego? Bo to zadanie już rozwiązywaliśmy. Sprawdzamy wobec tego, sprawdzamy, sprawdzamy… zgadza się. Czy to znaczy, że rozwiązanie jest na pewno dobre? Nie, nie na pewno. Ale gdyby wyszło coś innego niż jedna piąta, byłoby na pewno źle.
***
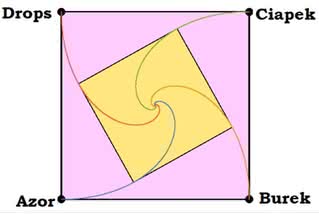
Nasza Basia z przedszkola stała się panną Barbarą, uczy się w Wojskowej Akademii Technicznej, bo będzie żołnierzem. Jeszcze ze szkoły zapamiętała historię o czterech wesołych pieskach. Nazywały się Azor, Burek, Ciapek i Drops. Siadły sobie w czterech narożnikach kwadratu. Nagle zaczęły się gonić. Azor pobiegł w stronę Burka, Burek w stronę Ciapka, Ciapek na Dropsa, a Drops na Azorka. Biegły z tą samą prędkością. Każdy z nich biegł wobec tego po specjalnej krzywej, jak na rys. 11, w każdej chwili psy znajdowały się w wierzchołkach zmniejszającego się i obracającego kwadratu. Wreszcie wpadły na siebie i nastąpiła wesoła zabawa. Basia uśmiechnęła się… i usłyszała poważny głos profesora.
– Dyktuję zadanie do domu. W czterech bazach wojskowych, tworzących kwadrat, znajdują się cztery rakiety: A, B, C, D. Odpalono je jednocześnie. Każda kieruje się według programu „leć na następną”, a więc A na B, B na C i tak dalej. Lecą z tą samą prędkością. Oblicz, po jakim czasie zlikwidują się wzajemnie w środku. Prędkość i odległość baz znasz.
Jeszcze raz uśmiechnęła się do siebie starsza szeregowa Barbara.
„Mam wolny wieczór, bo to zadanie umiem rozwiązać. Już w liceum mieliśmy zadanie: znajdź przedstawienie parametryczne tej krzywej. A właściwie to już w szkole podstawowej o tym było, tylko wtedy nie wiedziałam, że to się tak nazywa. Znam równanie, znam wzór całkowy na długość łuku krzywej. Wystarczy podstawić i obliczyć. To się szybko zrobi.”
Wyjęła telefon.
– Jacku, jesteś? Tak, możemy iść do kina!