SU DO KU czyli SpróbUj DOKąd Umiesz

Podejdę do gry zresztą nie tyle od strony matematycznej, co edukacji matematyki. Pokolenia dydaktyków wołały, że równie ważne jak rozwiązywanie zadań przez uczniów jest samo ich układanie. Oczywiście chodzi o zadania ciekawe, przemyślane i kształcące.
Zdrowy rozsądek każdego z nas chętnie się z tym zgodzi. Jechałem pięć razy do Kozienic autobusem. Za szóstym razem, gdy poruszałem się własnym samochodem, na co drugim skrzyżowaniu stawałem i wahałem się: w lewo, czy w prawo. Młodszemu pokoleniu wyjaśniam, że kiedyś nie tylko nie mieliśmy GPS, ale i mapy były trudno dostępne, a oznakowanie dróg pozostawało bardzo marne. Wracając do tematu, hasłem artykułu jest: nie graj w znane, ale stwórz własne sudoku.
Nie wprost, czyli alibi
Przypomnę, o co chodzi. W diagram złożony z dziewięciu kwadratów 3×3 należy wpisać liczby od 1 do 9 w ten sposób, by nie powtarzały się one ani w rzędzie (poziomym), ani w kolumnie (pionowej), ani w dziewięciu małych kwadracikach. Używając znanego obecnie uczniom terminu, mają tam stać permutacje liczb od 1 do 9.
W konkretnym zadaniu w kwadracie jest już kilka albo kilkanaście liczb. Wystarczy uzupełnić. Ogólnie, im więcej liczb jest podanych, tym łatwiej. Oczywiście nie zawsze. Sudoku jest szkołą logicznego myślenia. Wykorzystuję je w Wyższej Szkole Informatyki Stosowanej i Zarządzania, stworzonej pod auspicjami Polskiej Akademii Nauk.
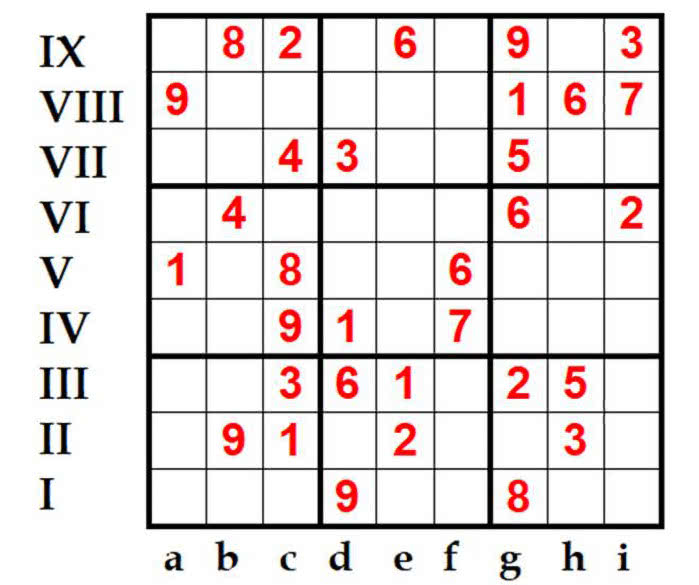
Do wyjaśnień wezmę sudoku zamieszczone w magazynie "Wiadomości RTV" z 27 grudnia 1999 r. (1). Jest to łatwy diagram. Przyjrzyjmy się rozumowaniu.
Spójrzmy na pole III-i (prawy dolny kwadrat). Wykażę, że stać tam musi liczba 9. Dlaczego?
Najpierw zauważamy, że "zajęte" są już 1, 3, 6 (bo stoją w rzędzie III). Następnie widzimy, że zajęte są 2, 3, 7 z kolumny i, wreszcie - 2, 3, 5, 8 (bo są w tym kwadracie). Zostaje więc 4 albo 9. Wykażę, że nie może to być 4, czyli pozostanie 9.
Przypuśćmy, że w polu III-i postawiliśmy 4. Zatem w rzędzie III dziewiątka musi być na jednym z wolnych miejsc a, b, f. Jednak w obu małych kwadratach w rzędach 1-3 jest już dziewiątka. A zatem nie byłoby jej gdzie postawić. Otrzymana sprzeczność kończy dowód tego, że w III-i nie może być czwórki, musi być więc dziewiątka.
Odnieśliśmy pierwszy sukces - pierwsze pole odgadnięte! Dokończ, Czytelniku. To naprawdę łatwy diagram. A ja zwrócę uwagę na sposób dowodu. Zastosowaliśmy nieskomplikowane rozumowanie nie wprost. Aby udowodnić, że zachodzi jedna z dwóch możliwości, przyjmijmy na chwilę jedną z nich. Jeżeli uda nam się wykazać, że jest ona niemożliwa, zostaje druga.
To bardzo piękny sposób rozumowania. Prawnicy nazwaliby go procesem poszlakowym. Przykład? W klasie lekcyjnej stłuczono żarówkę. Wszyscy uczniowie, poza jednym, mają alibi. Ukarany zostaje ten ostatni. Czy udowodniono mu winę? Matematycznie tak. Z ludzkiego punktu widzenia - nie. Stosujmy rozsądnie logikę matematyczną w życiu codziennym. Dowody nie wprost to potężna siła w matematyce. Na ogół są piękne właśnie dlatego, że najpierw "bujamy w obłokach" i dopiero po pewnym czasie schodzimy na ziemię. Zasługują na oddzielne opracowanie. Ale wykracza to poza ramy naszego kącika matematycznego, zwłaszcza bieżącego.
O przedszkolu słów kilka
Wydawać by się mogło, że ta popularna od kilkunastu lat w Polsce zabawa umysłowa jest starym japońskim ćwiczeniem umysłu, opartym na specyficznego rodzaju wyobraźni liczbowej. Że np. edykt cesarza Huranagure z XI wieku stanowił, iż kto z samurajów nie jest dostatecznie sprawny w sudoku, ma popełnić sepuku. Nic z tych rzeczy! Sprawa jest całkiem nowa. Grę wymyślił Amerykanin Howard Garns w 1979 r., pod prozaiczną nazwą "Number Place", ale dopiero ok. 2005 r. udało się jej (grze) zyskać szeroką popularność międzynarodową. A ja zainteresowałem się nią bliżej dopiero teraz.
Wykorzystam okazję i przedstawię grę tak, by Czytelnik zrozumiał różnicę między łamigłówkami (nawet najbardziej skomplikowanymi) a matematyką (nawet bardzo łatwą). W tym artykule: jak ułożyć sudoku, jak ustawić liczby, na ile sposobów można to zrobić?
Zaczniemy od przedszkola. Dla ustalenia uwagi: przez układ sudoku będę rozumiał pełny diagram zbudowany zgodnie z regułami. Teraz tylko o budowaniu takich pełnych diagramów.
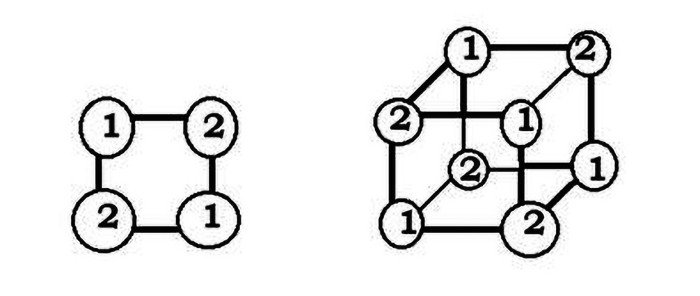
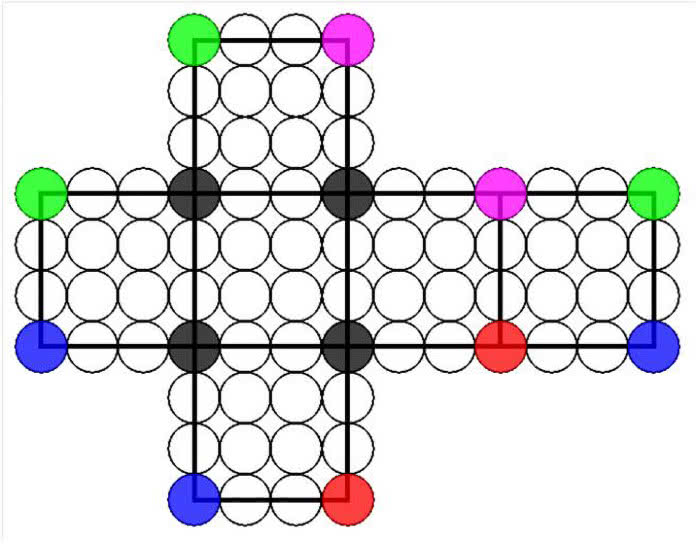
Zadanie 1. Sudoku z dwiema liczbami. W widoczne na rys. 2 kółeczka wpisz liczby 1, 2 tak, żeby nie powtarzały się ani "w poziomie", ani w pionie. Na ile sposobów możesz to zrobić? A w sześcianie? Łatwe zadanie? Oczywiście, że… łatwe. Wszyscy od razu widzą taki sześcian, prawda?
Nie będę tu wprowadzać Czytelnika w geometrię przestrzeni wielowymiarowych. Innym razem. Zaznaczę tylko, że równie łatwo jest zapełnić zgodnie z regułami sudoku jedynkami i dwójkami wierzchołki kostki dowolnego wymiaru n. O tym za miesiąc.
Czworościan foremny zna każdy - to taka piramidka (ostrosłup prawidłowy) o podstawie trójkątnej. Czy można w jego wierzchołki wpisać liczby 1, 2 tak, by każda krawędź była "różnoimienna"? Nie można. Łatwe uzasadnienie każdy znajdzie. Ale za dużo wymagamy. Nie uda się to nawet z trzema liczbami.
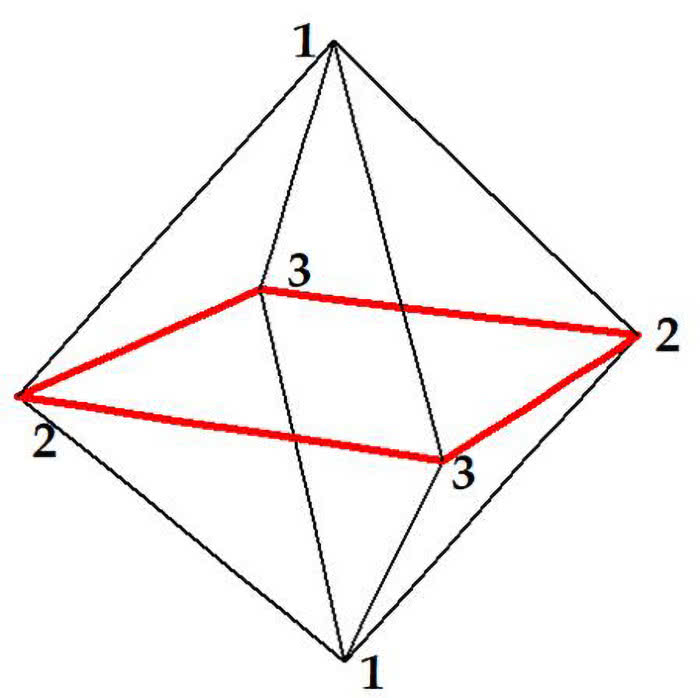
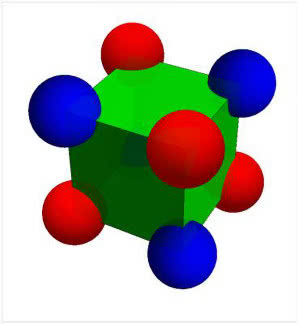
Trzy liczby wystarczą na ośmiościan foremny. To ładna, estetyczna i niedoceniana bryła (3).
Zadanie dla licealistów: ile jest możliwych układów takiego sudoku na ośmiościanie?
Rozwiązanie. Liczbę w pierwszym wierzchołku możemy wybrać na cztery sposoby. Przyjmijmy, że wybrano 1 tak, jak na rys. 3. Wtedy w kwadracie stanowiącym "równik" naszej bryły możemy postawić dwie dwójki i dwie trójki. I tylko tyle mamy stopni swobody. Osiem.
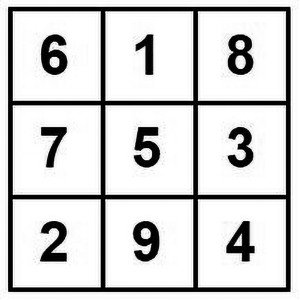
Dziewięć liczb możemy ustawić tak jak na rys. 4, w kwadrat magiczny. To kwadrat, w którym sumy liczb w pionie, poziomie i po przekątnych są równe. Tę wspólną sumę nazywamy sumą magiczną kwadratu. Teoria kwadratów magicznych była bardzo popularna w XIX wieku. Obecnie znów wraca do łask matematyków, a to oczywiście za sprawą komputerów. Zostawiamy jednak na inne czasy wycieczkę do kwadratów magicznych.
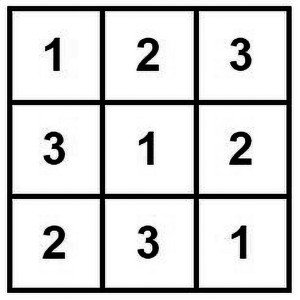
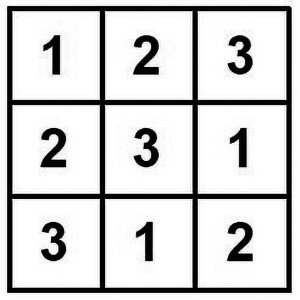
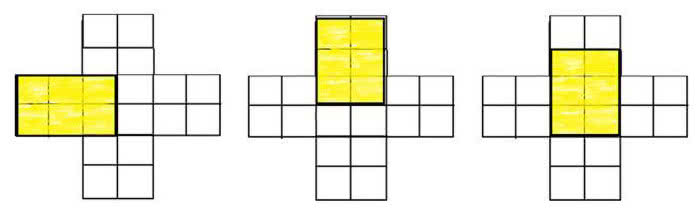
Dzieci przedszkolne ułożą sudoku z trzech liczb (5).
Zadanie. Czym się różnią diagramy z rys. 5? Jak możemy otrzymać jeszcze inne?
Skok na mikrokurs
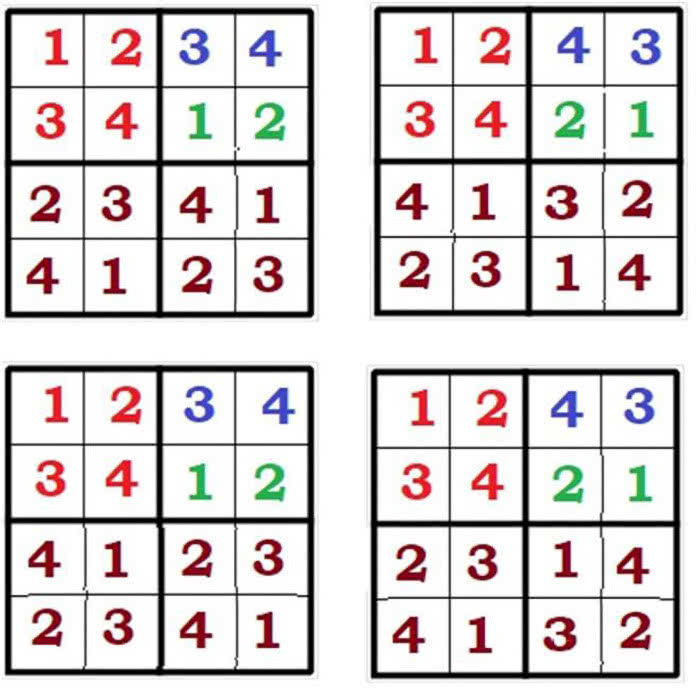
Przejdźmy do bardziej skomplikowanej konfiguracji: cztery liczby na szesnastopolowej planszy. W każdym małym kwadracie mają stać wszystkie liczby 1, 2, 3, 4 i żadna z nich nie może się pojawiać dwukrotnie w rzędzie poziomym ani pionowym. Najpierw sprawdźmy, czy potrafimy liczby tak umieścić? A jeśli tak, to na ile sposobów? I tu zaczyna się już matematyka, na poziomie uniwersyteckim.
Diagramy takie jak na rys. 6 łatwo zbudować, posługując się tylko prostą logiką. Matematyk chciałby jednak mieć algorytm - sposób nadający się do zaprogramowania. Najlepiej, żeby był tak ogólny, by dało się go zastosować w innych, bardziej skomplikowanych zadaniach. W końcu po to mamy współczesne "mówiące narzędzia" (tak w starożytności określano niewolników) - nasze notebooki, laptopy i smartfony.
Pewien uczeń zapytał nauczyciela:
- Czy kiedykolwiek użyję tej algebry, którą mi pan tak wtłacza do głowy?
Nauczyciel nie stracił rezonu:
- Ty może nie, ale ktoś bardziej rozgarnięty od Ciebie na pewno tak.
Jak wszyscy wiemy, komputery żyją w świecie czarno-białym, zero-jedynkowym. Albo coś jest, albo nie ma. Modą i nakazem współczesności jest, by przekładać wszystko na ciąg zer i jedynek. Mamy do tego nawet i stosowny urząd (Ministerstwo Cyfryzacji). Malarstwo Rafaela i Rembrandta, symfonie Beethovena, "Pan Tadeusz", wideo z Adamem Małyszem skaczącym po Puchar Świata (choć jeszcze nie sam Małysz, jako człowiek), ciśnienie atmosferyczne i sterowanie Jumbo Jetem - wszystko to tylko ciągi zer i jedynek.
Te górnolotne dygresje ułatwią mi przejście do mikrokursu matematyki, a konkretnie początków współczesnej algebry.
Symbolem Z2 oznaczamy zbiór złożony tylko z zera i jedynki. Matematycy mówią "grupa Z2". Chociaż ona taka mała, można w niej dodawać liczby. Po prostu 1 + 1 = 0. To znane choćby ze słyszenia dodawanie boolowskie (George Boole, matematyk angielski połowy XIX wieku). Często zamiast "zero-jedynkowe" mówimy właśnie "boolowskie". Trudno się z tym nie zgodzić: jeżeli dwukrotnie (w pewnym odstępie czasu) naciśniemy klawisz kontaktu elektrycznego, będzie znowu ciemno.
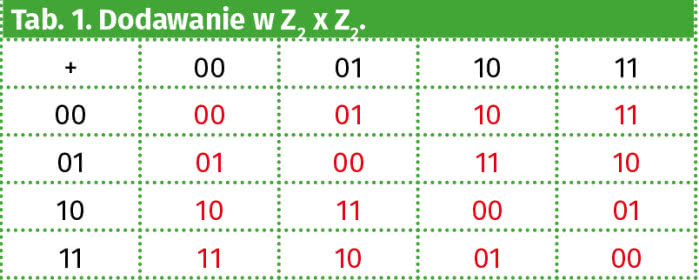
Teraz rozpatrzmy coś, co matematycy nazywają iloczynem prostym dwóch kopii Z2. To jakby płaszczyzna, gdzie na obu osiach mamy tylko dwie liczby: 0 i 1. Jak dodajemy pary (a, b), gdzie a i b są tylko zerami albo jedynkami? Tak, jak w tabelce 1.
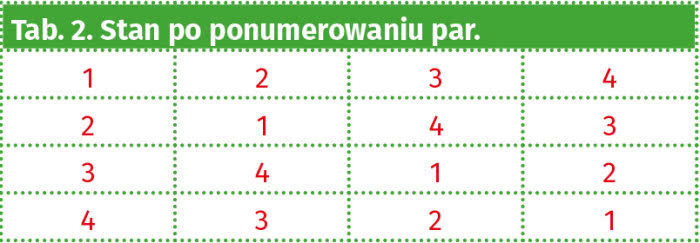
Ponumerujmy teraz pary: 00 to nr 1, 01 - nr 2, 10 - nr 3, 11 - nr 4. Wnętrze tabelki 1 zmieni się na:
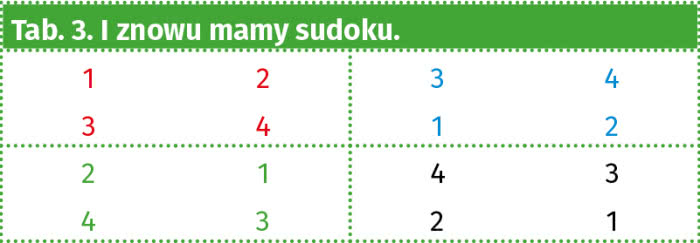
To jeszcze nie ustawienie sudoku. Ale zamieńmy drugi wiersz z trzecim (i pokolorujmy dla efektu). Teraz się zgadza: wszędzie, gdzie trzeba, są różne liczby.
To nic, że takie proste. Może nasz algebraiczny algorytm będzie działać i dla prawdziwego sudoku? Uprzedzając treść przyszłego artykułu: tak. Będziemy musieli tylko wejść głębiej w teorię grup.
Jak widać, na razie uczymy się układać stosowne konfiguracje. O odgadnieniach - potem.
W poszukiwaniu myślenia
Ucząc matematyki, chcemy uczyć myślenia, patrzenia na świat w kategoriach "O, jakie to ciekawe!", ale też i szukania analogii, podobieństw i przeciwnie, analizy różnic. Sam się zdziwiłem, gdy odkryłem analogię "trójkątnego sudoku" ze znanym zadaniem Hugona Steinhausa, matematyka najpierw lwowskiego, potem wrocławskiego. W jego wielokrotnie wydawanej książeczce "Sto zadań" znajduje się takie oto:
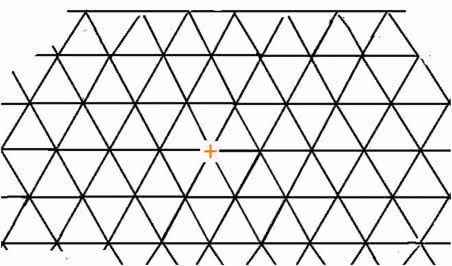
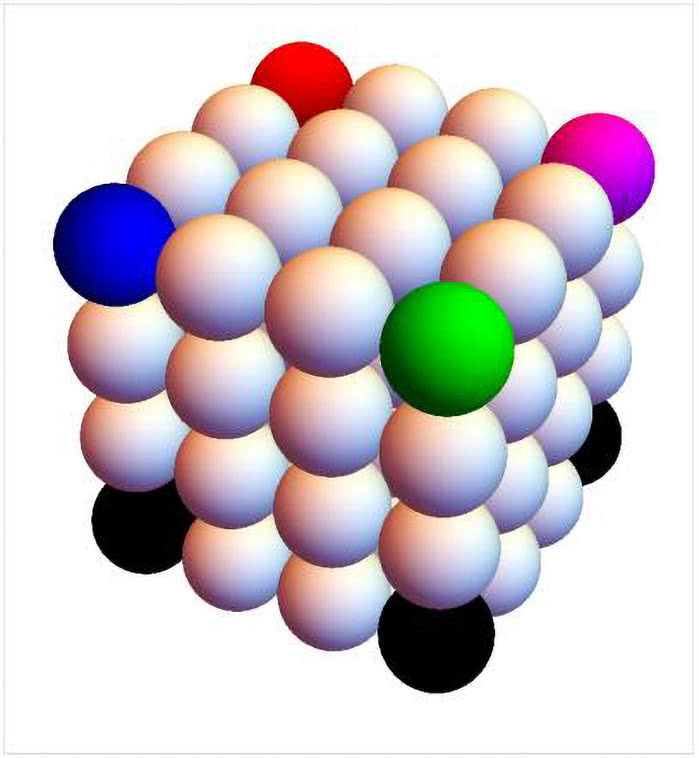
Płaszczyzna pokryta jest siecią trójkątną (rys. 8). Czy można w wierzchołkach tej sieci postawić znaki "plus" albo "minus" tak, by zawsze spełniona była zasada: jeżeli w dwóch wierzchołkach trójkąta stoją różne znaki, to w trzecim jest "minus", a jeżeli te same, to "plus"? Oczywiście można dać wszędzie "plus", ale to trywialne rozwiązanie odrzucamy.
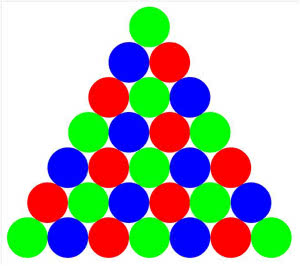
Rozwiązanie. Spójrz na rys. 7 i przypomnij sobie, że kolor czerwony to "ciepło", a niebieski i zielony - "zimno". Postaw "plus" tam gdzie ciepło, a "minus", gdzie zimno.
***
Na razie uczyliśmy się tylko układać sudoku, tj. wypełniać różne figury liczbami tak, by powstała stosowna konfiguracja. Znajdź inne ciekawe układy. Zaprojektuj własne sudoku. Może na dwunastościanie foremnym? Czy będzie ciekawe? Nie wiem.
***
W dniach 7-10 lutego obradowała w Toruniu 29. konferencja nauczycieli matematyki. Wszyscy właściwie zgadzali się, że jest źle. Że mimo deklaracji, szkoła wciąż nie uczy myślenia i że nie wiadomo, dlaczego tak jest. Jak pisałem, próbuję odrobić te zaległości i moich studentów z całą powagą zapędzam do sudoku. A jako signum temporis, czyli znak czasu, taka oto obserwacja.
Na jednym z referatów na wspomnianej konferencji wykładowczyni przez dwadzieścia minut zachwalała swój projekt, jak gdyby była to reklama telewizyjna. Nie powiedziała ani grama konkretu. Na moje pytanie, że może by jednak podała przykład efektów swojego działania, odpowiedziała:
- Wszystko znajdzie Pan na stronie.
To jest ów znak czasu: wszystko znajdziemy na odpowiedniej stronie. Taki rozwój dyskusji naukowych przewidział (jak i cały Internet) twórca literatury science fiction, niesłusznie nieuhonorowany Nagrodą Nobla Stanisław Lem (1921-2006). Szczegóły w jego książce "Powrót z gwiazd". Taka jest i moja rada dla Czytelników: znajdźcie interesujące strony internetowe o matematycznej stronie sudoku. Za miesiąc wracam do tematu. Będzie dużo algebry abstrakcyjnej i geometrii wielowymiarowej.
Michał Szurek