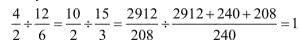Malarstwo, muzyka, matematyka

Nie odebrałem nigdy żadnego wykształcenia muzycznego, ale dość wcześnie polubiłem muzykę klasyczną. Słyszałem o tym, że podstawy teoretyczne muzyki to czysta matematyka, jednak nie interesowałem się tym głębiej.
Dopiero w mocno dojrzałym wieku zacząłem czytać podręczniki do harmonii oraz podręczniki akademickie z muzykologii. Przechodziłem więc to, co dzieci w podstawówce muzycznej - ale z pozycji dorosłego matematyka. Dlatego mogłem zobaczyć w teorii muzyki kwestie, których na ogół ani nie widzą, ani nie rozumieją zawodowi muzycy (choć, prawdę powiedziawszy, nie jest to im potrzebne do kunsztu, jaki osiągają).
Konstrukcja tzw. koła kwintowego przypomina porządek Gaussa użyty przez niego w konstrukcji siedemnastokąta foremnego. Zależności w tym kole (np. to, że tonika gamy durowej jest subdominantą następnej) przypomniała mi strukturę tabelki objętości i pól powierzchni kuli w przestrzeniach dowolnego wymiaru (pole powierzchni kuli wymiaru n mnożone przez 2πr daje objętość kuli w wymiarze n+2). Łatwo było mi też zrozumieć, co to znaczy matematycznie, że tercja jest podziałem harmonicznym kwinty. I tak dalej. Ale niech to nie zniechęci Czytelnika.
Sprawy, o których mówię, są dobrze znane muzykom - z praktyki. Przyznam, że zdziwiłem się, jak trudno przychodzi im zrozumienie podkładu matematycznego. Oni się z pewnością dziwili, że ja tak kiepsko przyswajam sobie podstawowe zasady harmonii.
 |
 |
| Fot. 1. Ilustracja twierdzenia Pitagorasa. W wersji dla uczniów najmłodszych: czy potrafisz z dwóch kwadratów zrobić jeden? | |
Muzyka jest piękna. Nie mam tu na myśli tzw. muzyki podprogowej, którą uwielbiają bywalcy dyskotek (a wiem, co piszę, bo raz byłem), ale tę, która trafia do nas ścieżką intelektualną - przede wszystkim europejską muzykę klasyczną, opartą na ugruntowanej przez wieki harmonii. Pytanie, jak wymierzyć piękno, nurtowało nas (ludzi) od zawsze i zajmuje do dziś. Jest to zagadnienie, które w humanistyce określa się mianem "problemu".
W matematyce "problem" to zadanie do rozwiązania. W humanistyce przeciwnie - tu problemu, niejako z definicji, nie da się rozwiązać (można go co najwyżej ująć inaczej): mamy więc "problem duszy ludzkiej", "zła i dobra", "idealnej organizacji życia społecznego" i wiele innych, a wśród nich właśnie piękna.
Sytuacja była bardziej klarowna do początku XX wieku, a więc do momentu, gdy ludzkość zaczęła odchodzić od antyku jako wzorca kultury. Do tego czasu zakładano, że "piękno" istnieje obiektywnie, a my poszukujemy go tak, jak zakopanego skarbu na wyspie. Powoli zaczęliśmy (my, ludzkość!) rozumieć, że tego skarbu nie ma, że może piękne jest… samo szukanie.
O ile zatem trudno jest określić, co znaczy "piękno", to gdy je spotkamy, nie mamy wątpliwości: "to jest to!". Musimy się też zgodzić, że wszystkie te kwestie są relatywne. O tym, że są ludzie lubujący się w hałasie, już pisałem. Podobno są i tacy, którzy nie widzą nic szczególnego w koncertach Bacha, Beethovena i Chopina. Piękne są Himalaje, Gorce i płaskie równiny węgierskie. Dla większości ludzi tenis jest grą nudną (tak jak dla mnie piłka nożna). Dla każdego jednak, kto trochę sam grał, tenis jest piękną, intelektualną grą.
O właśnie, wykorzystam wieloznaczność czasownika "grać". Muzyka europejska wzięła się z pomysłu Pitagorasa i jego szkoły filozoficznej (VI wiek p.n.e.). W dzisiejszej terminologii Pitagoras byłby uchodźcą. Pochodził bowiem z greckiej wyspy Samos, skąd uciekł przed tyranią Polikratesa, a swoją szkołę filozoficzną (dziś określono by ją mianem sekty) założył na południu Italii, w Krotonie, w dzisiejszej Kalabrii.
Imię Pitagorasa jest przede wszystkim kojarzone z twierdzeniem o sumie kwadratów przyprostokątnych. Uchodzi ono za najsłynniejsze w matematyce. Niech tak zostanie, choć Pitagoras ani nie odkrył tej zależności w trójkącie prostokątnym, ani nawet nie podał pierwszego dowodu. Odegrał jednak w historii myśli europejskiej rolę stokroć ważniejszą. Mówiąc dzisiejszym językiem, zastanawiał się, czym się różni człowiek od zwierząt. Próbował nawet dostać na te swoje badania grant z Brukseli, ale podanie zostało odrzucone z przyczyn formalnych. Odpisano, że nie ma takiego miasta, jak Bruksela, a Europa nie jest żadnym kontynentem, ani unią państw, a piękną królewną tyryjską, córką Agenora, później królową kreteńską, porwaną i uwiedzioną przez Zeusa…
Żarty żartami. Rozkwit szkoły pitagorejskiej przypadł na lata ok. 580 p.n.e. Nie tylko nie znano wówczas radia, samochodów, telefonów komórkowych, coli, ale i ziemniaków, kawy, herbaty i papierosów! Dopiero za pięć wieków miał się narodzić Jezus, a za 1500 lat Mieszko Pierwszy. Rzym nie dorósł jeszcze do potęgi imperialnej.
Od muzyki do geometrii, albo odwrotnie
Na lekcjach matematyki w szkole rysujemy bryły w perspektywie równoległej. To wygodny, inżynierski sposób. Ale oglądamy wszystko w perspektywie zbieżnej. Nie obawiamy się wsiąść do pociągu, nawet wtedy, kiedy widzimy, że tory zwężają się aż pod horyzont. Z doświadczenia wiemy, że jadący pociąg je sobie "rozepchnie".
Perspektywa zbieżna ma i wady, które szczególnie wychodzą przy "selfi" - przerysowanie i wyolbrzymienie pierwszego planu. Przy fotografii budynków występuje efekt walących się kolumn: na fot. 2 mamy wrażenie, że dom się przewraca do tyłu. Nie ma rady - skoro mamy zmieścić trzy wymiary w dwóch - zawsze coś musi się nie udać.
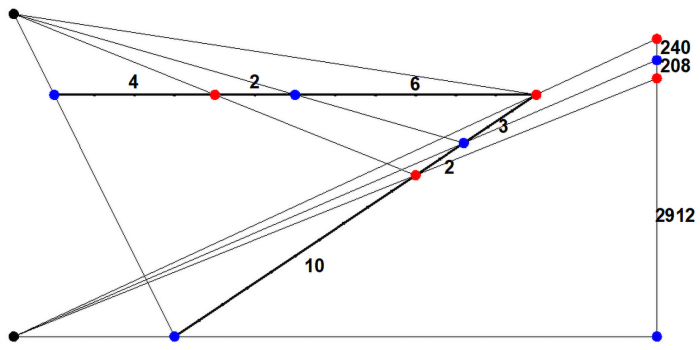
Wszystko to wynika właściwie z geometrii, a dokładniej z jednej cechy rzutowania centralnego. Widzimy to dobrze na fot. 3. Geometryczny środek czerwonej linii nie jest w połowie drogi do lasu. W języku geometrii można wyrazić to tak: środek odcinka nie jest niezmiennikiem rzutowania środkowego.
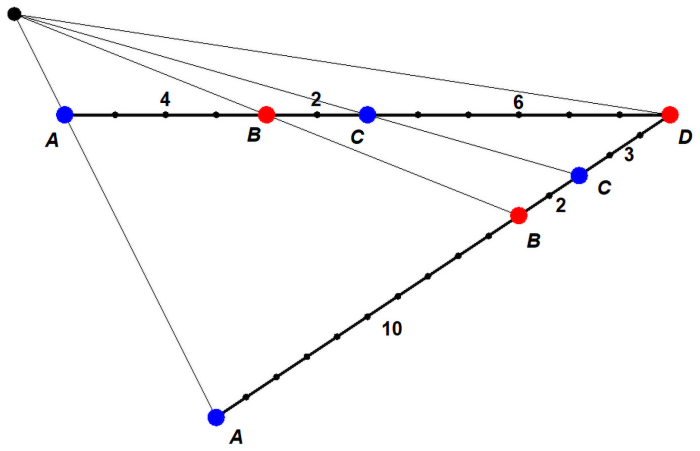
Renesansowi malarze odkryli, że już w I wieku naszej ery Pappus pokazał, co jest takim niezmiennikiem. Na prostej obieramy dwa mocpunkty, niech nazywają się A i C… To, co nie zmienia się przy rzutowaniu środkowym odcinka AB, jest ilorazem dwóch ilorazów. Można to zrozumieć tak. Spójrzmy na rys. 1. Mamy na nim "niebieski" odcinek AC.
Punkt B dzieli go w stosunku 4:2, czyli dwa do jednego. To jasne. Czy jest jeszcze inny punkt, który dzieli ten odcinek w tym samym stosunku? Tu matematyka płata figle. Jeżeli napiszemy stosowne równanie i rozwiążemy je, wyjdzie nam jeszcze jeden, inny punkt: punkt D. Czy można jednak o nim powiedzieć, że "dzieli odcinek AB"? Może i nie, ale faktem jest, że stosunek odległości tego punktu do końców odcinka AC wynosi 12:6, czyli 2, tyle samo, co dla punktu B. Mówimy wtedy, że B i D dzielą odcinek AC harmonicznie (starsze, zapomniane określenie: "dzielą w stosunku skrajnym i średnim"). "Harmonicznie" - a więc mamy jakiś związek ze sztuką, z muzyką przede wszystkim.
Muzyka… młotów
Gdzie tu muzyka? Ależ to jest właśnie muzyka! Żeby to zrozumieć, wróćmy do Pitagorasa! Według legendy, Pitagoras stworzył swoją skalę muzyczną, przysłuchując się dźwiękom wydawanym przez młoty w kuźni. Doszedł do wniosku, że to da się wyrazić zależnościami liczbowymi, zgodnie zresztą z ogólnym przekonaniem, że wszystko pochodzi od zależności liczbowych. Pięknie to opisał ks. Józef Tischner w swojej "Filozofii po góralsku" (wyd. Znak, 1997). Pitagorasem jest tam konkretny góral, Jędrek Waksmundzki. Założył on szkołę. Pierwszą szkołę na świecie, czyli (jak pisze ksiądz Tischner) na Podhalu. Ksiądz Tischner próbuje oddać w piśmie gwarę góralską i daje to taki efekt:
Dostać sie do tyj skoły nie było łatwo. A wytrzimać, jesce trudniej! Pirsy rok obowiązywało: słuchanie i góralski tóniec. Cymu słuchanie? Cymu tóniec? Tymu słuchanie, coby sie nikt głupio nie pytoł. (…) A góralski tóniec był wozny bez to, ze sie go tońcy po dwa, po śtery a nawet po sesnoście. A to jest telo piekny tóniec, ze na niego ni ma ceny. A cyfra jest. Cyfra za cyfróm. I to sie nazywo "cyfrowanie". Tóniec na cyfrowaniu stoi. A Pitagoras, czyli Jędruś Waksmundzki wywiód, ze ni ino tóniec, ale i cały świat to jest je nic inksego, ino jedno wielgie cyfrowanie. (…) A syćko zacyno się od muzyki. Bo na Zorębek przychodziyli muzykanty. I grali. A on słuchoł. A usłysoł nie ino to, ze w muzyce gro sie po dwa, po śtyry, cy po sesnoscie. Jędruś Waksmundzki usłysoł oktawy, kwinty, kwarty. To juz cosi znacy. Co? Znacy, ze cyfra cyfruje. Chces mieć róźnice między dźwiękami, weź strune długóm abo krótkóm. Mozes tyz wziąć hrubóm abo cienkom. Nie cujes, ze cyfra cyfruje? Razu jednego seł nas podhalański Pitagoras z ryb koło kuźnie. Była kuźnia w Łopusnej blisko Dunajca. A w kuźni kowole kuli. Słychać było: dzyń, dzyń, dzyń. A coz było widać? Widać było i słychać tyz ze róźnica dźwięków brała sie z róźnicy młotów. Cięzki młot to dźwięk jakisi taki hrubsy, lekki młot - to dźwięk jakisi taki cieńsy. Nie cujes, jak cyfra cyfruje? (…) Ej, mocny Boze. Cyfry nie ino to robią, ze świat jest cyfrowany, one tyz cyfrują same siebie.
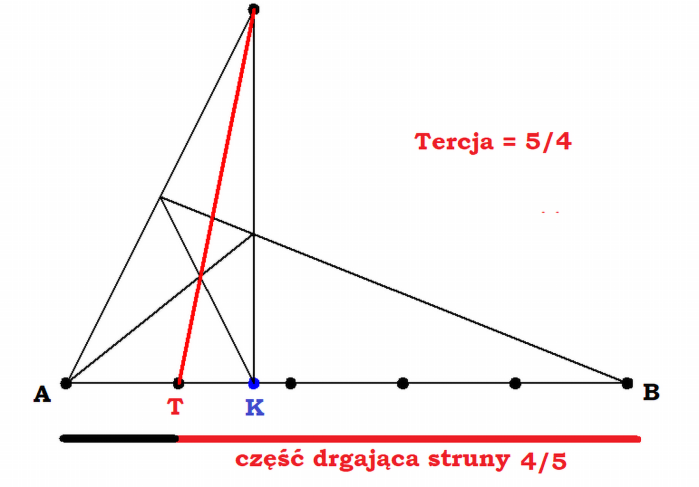
Jak było, tak było, w każdym razie Pitagoras zaobserwował, że skrócenie dźwięczącej struny o połowę daje "ten sam dźwięk, tylko wyższy". Tak słyszymy, tak to odbiera nasze ucho. Dźwięk o dwukrotnie zwiększonej częstotliwości odbieramy jako "ten sam, tylko wyższy" - dobra jest analogia z figurami podobnymi: są to "takie same" figury, tylko w innej skali. Spójrzmy na rys. 3 - jest to znana w matematyce konstrukcja "czwartego harmonicznego". Dzielimy odcinek AB harmonicznie tak, żeby trzecim punktem był C. Co to jest z muzycznego punktu widzenia? Czytelnikom z ukończoną podstawową szkołą muzyczną przypomnę: to jest podział harmoniczny oktawy, a więc kwinta. Drgająca część struny zaznaczona jest u dołu na czerwono. Strunę AC skrócił Pitagoras o jedną trzecią (AK). Zabrzmiała kwinta! Skąd "pięć" w nazwie? Stąd, że drga (a więc wydaje dźwięk) dwie trzecie struny. Ze znanych dzisiaj praw fizyki wiemy, że częstotliwość takiego dźwięku to 3/2 dźwięku całej struny.
Goethe (tak, ten poeta niemiecki, którego najbardziej znanym utworem, dziełem pisanym przez kilkadziesiąt lat, jest oczywiście "Faust") miał kilka udanych powiedzeń o matematykach. Jedno z nich mówiło, że matematycy są jak zakochani: podaruj takiemu jedną przesłankę, a wyprowadzi z niej całą wiedzę na twój temat. Z jednej zależności kwintowej, z jednego podziału harmonicznego, wyprowadził Pitagoras (a raczej jego następcy) całą muzykę europejską, z Bachem, Beethovenem i Brahmsem - artykuł jest o trzech M, więc podaję tu trzech znanych muzyków na B. Czy mieszczą się tu The Beatles? Tak. Ich muzyka to "jeszcze" muzyka klasyczna, posłuchajmy choćby "Yesterday", "All You Need is Love", a nawet niesamowitej "Żółtej łodzi podwodnej" - którą moje pokolenie z lubością przekręcało na żołtyj parochod, sowietskij parochod. Czy współczesna muzyka "pop" ma coś wspólnego z klasyczną? Nie wiem. Próbowałem słuchać, ale było za głośno…
Do muzyki i matematyki wrócę niebawem.
Michał Szurek