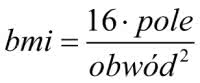Kolorowa matematyka

Tekst jest niejednolity - zaczynam od pogadanki dla małych dzieci, ale przerzucam się na rozważania dla dorosłych i z powrotem. To żeby nie zanudzić. Najpierw dla dzieci. To mój głos w dyskusji, jak należy (no, jak można) mówić maluchom o "Królowej Nauk".
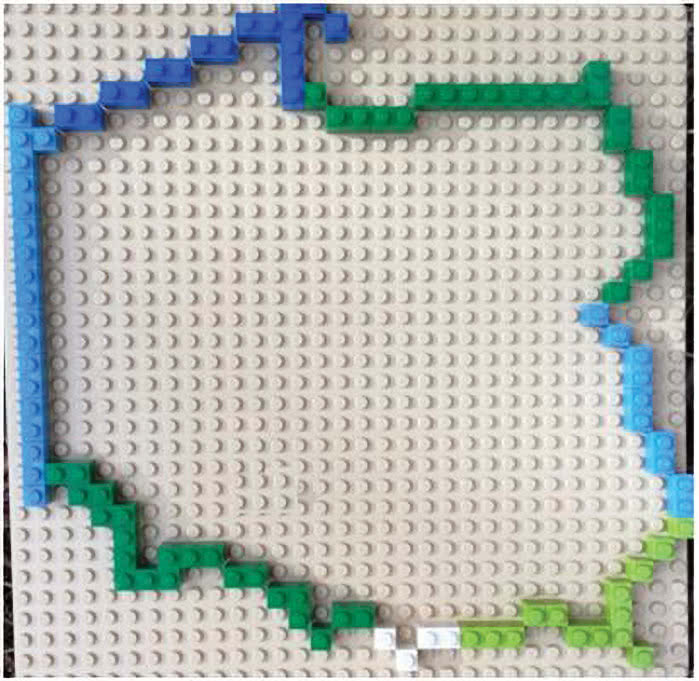
Zadanie 1. Spójrz na moją pierwszą układankę. Co na niej widzisz?
Gdzie mieszkasz? Zaznacz. Jak myślisz, czy kolory naszych granic wybrałem przypadkiem, czy znajdziesz może uzasadnienie, dlaczego "na górze" jest niebiesko i zielono, a "na dole" biały kawałek? Ale dlaczego napisałem "na górze" i "na dole"? Przecież te strony świata nazywają się …no, właśnie jak? A te dwie pozostałe? A może wiesz, dlaczego międzynarodowymi oznaczeniami czterech stron świata są N, E, W, S ?
Zadanie 2. Spójrz na znaki drogowe (1). O których możemy powiedzieć, że są kwadratowe? A dlaczego pierwszy i trzeci mają zaokrąglone narożniki? Dowiedz się, jakie znaki drogowe mają kształt trójkątny, okrągły (kolisty) i ośmiokątny. Dlaczego jeden znak trójkątny jest inny niż inne? Dlaczego jest tylko jeden znak ośmiokątny?
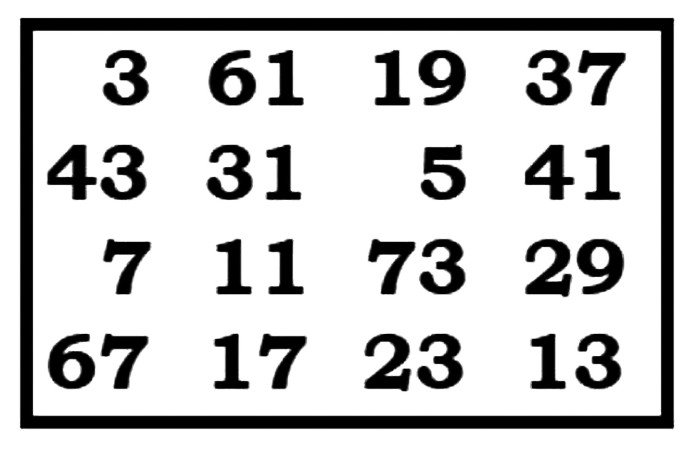
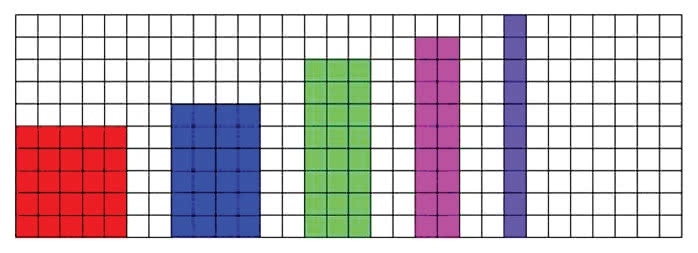
Zadanie 4. Teraz spójrz na moją układankę numer 2. Czy widzisz w niej kwadraty? Na pewno - to te czerwone w środku. Są coraz większe. Pierwszy z nich, malutki, po lewej - ma jedno oczko, jeden "guziczek".
Odpowiem od razu. Magiczny kwadrat liczbowy to taki, że sumy liczb w poziomie, w pionie i po przekątnych są takie same. Sprawdźmy:Pewnie powiesz, że drugi jest dwa razy większy, bo ma dwa guziczki na każdym boku…. Oj, czy naprawdę jest dwa razy większy? Policz, ile ma "guziczków" Cztery! Zobaczmy, co dalej. Trzeci jest szeroki i wysoki na trzy oczka. Policz oczka. Ile ich jest? Dziewięć. Czwarty jest długi na cztery i szeroki (albo wysoki) też na cztery. Cztery razy cztery to szesnaście. Tak jest, ma szesnaście oczek. A piąty? Każdy bok ma pięć oczek, no to razem jest ich, ile? Brawo, 25. Mówimy, że kwadrat ten ma pole równe 25. Ale to na pewno wiedziałeś. Czyli to tak jak przedstawiono w tabeli obok.
4+9+2=3+5+7=8+1+6=4+3+8=9+5+1=2+7+6= 4+5+6=8+5+2=15.
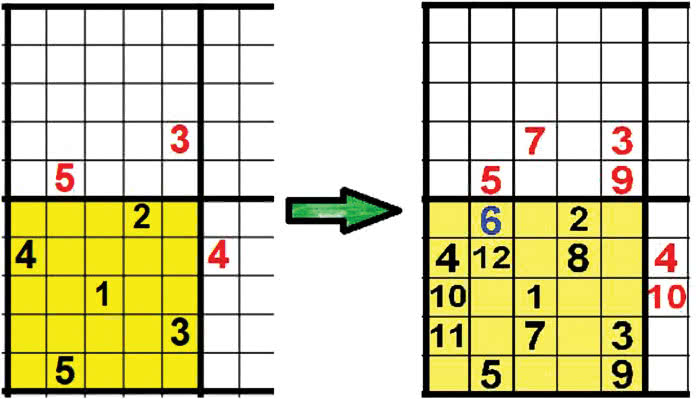
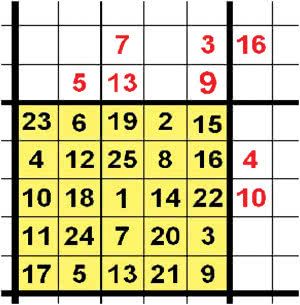
Słusznie pisze Wikipedia, że kwadraty magiczne nie mają zastosowań w nauce. Są tylko ciekawe. Ale ciekawszy od samych kwadratów są sposoby ich budowania. To tak, jak z turystyką: bardzo często cel jest drugorzędny, a ważna jest droga do niego. Spójrzmy jak zbudować kwadrat dwudziestopięciopolowy. Stawiamy jedynkę w środku i przypominamy sobie zapomnianą już nieco "królewską grę", czyli szachy. Będziemy skakać konikiem w górę w prawo, na NNE (północ-północ-wschód). Już "trójka" wypada poza kwadratem. Ściągamy ją na przynależne jej miejsce (ostatnie w drugim rzędzie od dołu). Przypomina to muzyczną "redukcję do pierwszej oktawy" - ten sam dźwięk, tylko o oktawę niżej. Tę zasadę stosujemy konsekwentnie … dopóki się da. Zacina się już przy szóstce. Nie szkodzi, stawiamy szóstkę pod czerwoną piątką, czyli już w obrębie naszego kwadratu.
Wracamy do matematyki dla dzieci. Spójrz teraz na górną część mojej układanki nr 2. Czy tam są kwadraty? Nie! Jak się nazywają takie figury? Beatko, jak? Masz rację, prostokąty. Dlaczego tak się nazywają? Bo mają kąty proste? Za chwilę sobie o tym pomówimy, ale na razie przypomnijmy sobie, co to jest kąt prosty. Bartku, jak byś to wytłumaczył komuś, kto nie wie? Może tak: że to taki równy kąt . No, niech będzie. Jeżeli jedziemy samochodem i skręcamy pod kątem prostym, to tak ani za bardzo do przodu, ani za bardzo do tyłu, tylko po prostu równiutko w bok. Celinko, wstań i obróć się o kąt prosty. W lewo, czy w prawo? W którą stronę chcesz.
Pomówmy jeszcze o tych figurach na górze, czyli prostokątach. Który z nich jest gruby, chudy, szczupły, wysoki, niski, mniej podłużny, bardziej podłużny? Na pewno zgodzisz się, że ten żółty po prawej jest długi, chudy i wysoki. Ale uważaj. Jeżeli on się położy na boku to też będzie długi, ale niski. Czy nazwałbyś go "grubym" ?
Teraz znów dwie wstawki dla starszych Czytelników. Pierwsza jest o liczbie 100. Chyba w każdym języku słowiańskim 100 to sto. Jest to ważne dla językoznawców. Nazwa tej liczby odróżnia bowiem dwie grupy języków indoeuropejskich, do których należą wszystkie języki na naszym kontynencie z wyjątkiem fińskiego, węgierskiego, estońskiego baskijskiego i mało znanego bretońskiego.
W językach, które ukształtowały się w pierwszej fali wędrówek ludów, prasłowo oznaczające 100, rozwinęło się do hekatón (greckie) i centum (łacińskie), skąd pochodzi zarówno fracuskie cent, jak i niemieckie hundert (i oczywiście angielskie hundred). Dlatego języki te określamy mianem kentumowych.
Nasz język należy do grupy języków centralnych, czyli satemowych, bo po palatalizacji ( zmiękczeniu) prasłowo przyjęło tę miłą i krótką formę sto. Sto lat, sto lat, niech żyje….
Druga wstawka jest dłuższa, ale jest jak najbardziej na temat.
Matematyk i Body Mass Index
Wskaźnikiem BMI zainteresowałem się z konieczności. Przypominam, że jest to wskaźnik porównujący i oceniający zgodność wagi dorosłego pacjenta z teoretycznie ustaloną normą. Formuła matematyczna jest prosta: dzielimy wagę (w kilogramach) przez kwadrat wzrostu (w metrach). Przyjmuje się, że granicą nadwagi jest iloraz 25. W tej skali znany tenisista hiszpański, Rafael Nadal, ma prawie nadwagę (185 cm, 85 kg), co daje BMI równe 24,85. Wychudzony jak szczapa jego rywal Serb Novak Djokovic, ma 21,79 i mieści się swobodnie w granicach normalnej wagi. Piszący te słowa ma … nie powiem, jak wysoki ten indeks. Natomiast jako dolną granicę prawidłowej wagi dla mnie (180 cm) jest … 61 kg . Facet o wzroście 180, ważący 61 kg , przewrócił by się chyba przy byle podmuchu wiatru. Uważam, że o ile sama zasada wskaźnika jest poprawna, to takie ustawienie parametrów zostało chyba wymuszone przez firmy farmaceutycznie (pigułki na odchudzanie).
Sami lekarze zdają sobie sprawę, że wskaźnik ten nie uwzględnia cech osobowych pacjenta. Ja dorzucę jeszcze fakt matematyczny. Starsi ludzie kurczą się. Osiada im kręgosłup. Ja w młodości mierzyłem 184 cm, teraz 180. Gdybym ważył 100 kg, to "wtedy", to znaczy przy wzroście 184 cm dawało by to wskaźnik 29,5 (nadwaga I stopnia), a teraz, to jest przy 180 cm było by 30,9 (nadwaga drugiego stopnia). A przecież "ja" nie zmalałem, tylko kręgosłup mi się wykrzywił.
Przetestujmy jeszcze wskaźnik BMI na "niezmienniczość miar". Chodzi o to, że powinno być wszystko jedno, czy dane podajemy w systemie metrycznym (kilogramy i metry), czy np. w funtach angielskich i stopach. Oczywiście liczby wyjdą różne, tak jak różne są liczby wyrażające prędkość na drodze w milach i w kilometrach. Ale z jednego da się łatwo przeliczyć na drugie, bez sprzeczności. Tu dygresja. Mile na kilometry przeliczyć łatwo. Ale na pytanie, jak wielką ma lodówkę, mój znajomy Kanadyjczyk odpowiedział "27 stóp sześciennych". I bądź tu mądry. Jeszcze gorzej jest z określeniem zużycia paliwa przez samochód. W USA i w Kanadzie podają to jako "ile mil przejadę na jednym galonie"?. Czytelniku, może potrafisz ocenić (obliczyć), czy 60 mil na jednym galonie to dużo, czy mało? A jeszcze galon amerykański różni się od kanadyjskiego (zwanego imperialnym). Co prawda w Kanadzie od wielu lat obowiązują miary metryczne, ale nie tak łatwo zmienić przyzwyczajenia.
Ale z BMI jest w porządku. Ponieważ stopa angielska to 30,48 cm, a funt to 0,454 kg, to angielski wynik BMI (wyrażony w funtach wagi na kwadrat liczby stóp wzrostu), trzeba pomnożyć przez iloraz 0,454 i 0,30482, czyli 4,88. Stukilowa osoba mierząca 180 cm ma 220,26 funta i 5,9 stopy. Oba sposoby obliczenia BMI dają to samo, 30,9.
Teraz najciekawsze (z punktu widzenia matematyka). W jednej ze swoich książek opisałem "wskaźnik okrągłości" - jak bardzo zaokrąglone figury są podobne do koła. Jak bardzo - to znaczy matematycznie "na ile procent". Koło ma oczywiście 100 procent "kołowatości". A inne figury? Jak to wymierzyć?
Zastosujmy ten pomysł do mierzenia, jak bardzo prostokąt "podobny jest" do kwadratu. Nazwijmy to "miarą pękatości". Kwadrat powinien mieć pękatość 100%, prawda? Matematyk woli mówić, że pękatość kwadratu jest równa 1, a wąskich prostokątów odpowiednio mniej.
Zastosujmy coś w rodzaju Body Mass Indeks dla prostokątów. Podzielmy pole przez kwadrat obwodu. Ile wyjdzie dla kwadratu o boku a ? To proste rachunki 1/16. Aby wskaźnik był równy 1, pomnóżmy przez 16. A zatem "body mass index" dla prostokątów to
Wyobraźmy sobie teraz, że prostokąty idą do lekarza. Zaraz obliczę wasze BMI, mówi pani doktor. Proszę po kolei. Już, oto wasze wyniki. Który ma schudnąć?
Wniosek. BMI traktuje człowieka jako istotę płaską! Wskaźnik ten dobrze się sprawdza (pomijając ustawienia poziomów granicznych). Jednak matematycy są sceptyczni. Jest to za proste, żeby mogło być uniwersalne. Zbyt proste formuły matematyczne na opisanie zjawisk biologicznych i społecznych należy traktować z bardzo dużą ostrożnością.
Wracamy do pogawędki dla młodszych dzieci. Jeszcze raz spójrzmy na układankę numer 2. Zgodziliśmy się, drogie dzieci, prawda, że prostokąt ma same kąty proste. Dziwne, gdyby było inaczej. Ale figury widoczne na dole (niebieska piramidka) , fioletowy "zakrętas" i błękitny wiatraczek też mają tylko kąty proste. To może są prostokątami? Nie, ludzie umówili się, że prostokąty to tylko takie, które mają cztery kąty proste, a nie więcej.
Naucz się myśleć poprawnie. Spójrz:
Jeżeli coś jest prostokątem, to ma same kąty proste. To nie to samo, co:
Jeżeli coś ma same kąty proste, to jest prostokątem.
Dlaczego? Weź zamiast "prostokąta" kotka i pieska, zamiast "kąty proste" weź "łapy". Czy teraz rozumiesz? Na pewno!
Komentarz dla dorosłych (i nie tylko). W latach mojej młodości istniał slogan: Myślenie ma kolosalną przyszłość! Szkoda, że … to było tak dawno.
Aha. Ważne pytanie. Czy kwadrat jest prostokątem? Jest! Ma cztery kąty proste! Można powiedzieć, że kwadrat to najrówniejszy prostokąt. Każdy bok jest tak samo długi.
Będziemy dalej tworzyć ładne układanki. Wiesz na pewno, co to jest liczba parzysta. Jeżeli klasa ustawi się parami, to albo ktoś zostanie bez pary, albo … nie zostanie. Czy 12 jest liczbą parzystą? Tak. Gdy dwanaście osób chce pograć w siatkówkę, łatwo im stworzyć dwie drużyny. Dwa razy sześć to dwanaście. A jeżeli te same osoby chcą pograć w ping ponga, to mogą utworzyć sześć par. Sześć razy dwa to też dwanaście.
Co mają wspólnego: mecz, ślub, pojedynek, lustro i moneta? Liczbę dwa. W meczu są dwie drużyny, ślub biorą mężczyzna i kobieta (tak, tak, mężczyzna i kobieta - on żeni się, ona wychodzi za mąż). W pojedynku walczy dwóch rywali, w lustrze widzimy jakby trochę innego ""ja. Moneta ma dwie strony. Jak się one nazywają? Orzeł i reszka. Na polskich monetach mamy rzeczywiście orzełka. Czy znasz kogoś, kto ma brata-bliźniaka albo siostrę-bliźniaczkę? Dawno temu na wsiach używano "dwojaczków " - dwa połączone naczynia, jedno na zupę, drugie na … drugie danie.
A może rozumiesz słowa: podwójny, symetria, odwrotność, dualność, przeciwieństwo, debel, duet, tandem, alternatywa, negatyw, zaprzeczenie ?
Jeżeli pokój ma dwa wyjścia (albo wejście i wyjście, jak wolisz), to czy powiemy, że ma "dwa drzwi"? Nie, jakoś nie tak. A jak jest poprawnie? A dlaczego tak mówimy? A jeżeli do pokoju dwudrzwiowego dobudujemy jeszcze jedno wejście i wstawimy tam drzwi, to ile drzwi będzie? Trzy? No, nie….
"Przód" chodzi w parze z "tyłem". Tam, gdzie jest "lewo", jest i "prawo", jeżeli coś nie jest "na górze"to może "na dole". Gdyby nie było plusa, to i minus byłby niepotrzebny. Piękna jest ta liczba dwa.
Zaśpiewaj: "Małe pieski dwa…." Czy znasz melodię? Jeśli nie, to się naucz.
Ile klocków jest na następnej układance? Nie wiem, nie będziemy nawet liczyć. Chodzi mi o to, że bez liczenia wiem, że jest ich parzysta liczba. Dlaczego? Kacperku, skąd ja to wiem? O, ty też już wiesz? Jak mówisz? Że wszystkiego jest po równo? Po tyle samo!
Równiutko. Do pary. Czy przeszkadza to, że po lewej kolor różowy jest ciemniejszy niż po prawej?
Co nie jest parzyste, jest nieparzyste. Pamiętam, że gdy w dzieciństwie grywałem w piłkę, zawsze był kłopot, jeżeli było nas siedmiu, dziewięciu, jedenastu, trzynastu… Nie dało się podzielić na dwie równe drużyny. Wyjściem było to, że graliśmy na jedną bramkę. Bramkarz nie należał ani do jednej, ani do drugiej drużyny. Miał bronić każdy strzał.
Zadanie … nie tylko dla dorosłych. Podaj przykłady pojazdów, które mają nieparzystą liczbę kół (zapasowego koła w samochodzie nie liczymy). Kiedyś zauważyłem, że może być nim … kolejka na Kasprowy Wierch - wagonik toczył się po linie nośnej na siedmiu kółkach. Ale teraz nie wiem, jak jest.
Ile jest klocków w czwartej układance? Czy jest ich parzysta, czy nieparzysta liczba? Piotrek, to do ciebie! Jak to rozwiążesz? Chcesz policzyć i wtedy będziesz wiedzieć? No tam, ale czy nie pomylisz się w tym liczeniu? Spójrz, czy jest wszystkiego po równo.
W starożytności liczby nieparzyste uchodziły za lepsze. Dziś wolimy parzystość. Czy wiesz, że jeżeli dajemy komuś kwiaty, to powinna być ich nieparzysta liczba? Oczywiście nie dotyczy to olbrzymich bukietów.
Zadanie do pomyślenia… może nie tylko dla dorosłych. Komu należą się dziś słowa uznania, kwiaty i szacunek nas wszystkich (i nie bójmy się tego - solidne wynagrodzenie!) za ich poświęcenie, wyczerpującą, długą, ciężką i ryzykowną pracę, żebyśmy nie zachorowali, a jeśli zachorujemy, to żeby jak najszybciej wyzdrowieć?
Michał Szurek