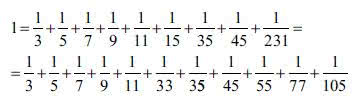Urok liczb nieparzystych

Żelazną zasadą numerowania domów przy ulicach jest, by po jednej stronie były "adresy" parzyste, po drugiej nieparzyste. W Warszawie obowiązuje zasada, że przy ulicach równoległych do Wisły parzyste są bliżej rzeki, a przy ulicach prostopadłych do Wisły - są po północnej stronie. Zasada ma zresztą wiele wyjątków. Wiele nerwów kosztowała mnie przygoda we wschodnim Berlinie, w roku bodajże 1983. Mój hotel był tuż przy murze. Numeracja zaczynała się po jednej stronie ulicy i szła co jeden (a nie co dwa), dochodząc do jej końca. Drugą stroną szła od połowy numerów aż do końca. Jak się potem dowiedziałem, był to stary zwyczaj niemiecki.

Aleją Krakowską w Warszawie jeżdżą tramwaje o numerach 7, 9, 15, a przy ulicy Hynka jest przystanek autobusów 141, 189 i 401. Sześć liczb nieparzystych. Nie znalazłem, kiedy ostatni raz w Totolotku wypadły same liczby nieparzyste. Prawdopodobieństwo tego jest trochę większe niż 1 do 26, czyli jeden do 64. "Trochę większe", bo liczb do wyciągnięcia jest 49, z czego nieparzystych "aż" 25, czyli więcej niż połowa. Takie losowanie (sześć nieparzystych) statystycznie powinno się więc zdarzać trochę częściej niż raz w roku. Natomiast 7 maja 2019 r. wylosowano same liczby parzyste: 2, 6, 8, 16, 36 i 48.

Deus impare numero gaudet - Bóg raduje się liczbą nieparzystą, mawiano w Starożytności. Teraz mamy inny gust. Lubimy, żeby było do pary. Mimo wszystko nie sądzę, aby zwyczaj dawania komuś nieparzystej liczby kwiatów (znany tylko w Polsce) pochodził z czasów rzymskich! Po angielsku liczby nieparzyste to odd numbers, czyli "dziwne". Po rosyjsku parzysty to cziotnyj, co przypomina staropolskie "cetno i licho". W pierwszej książce matematycznej po polsku Janusz Kłos używa terminu "przyszło w licho" (= otrzymaliśmy w wyniku liczbę nieparzystą).

Parzystość jest pożądana, nieparzystość sprawia kłopoty, chociaż z praktycznych względów lepiej jest, gdy w komisji mającej o czymś decydować zasiada nieparzysta liczba członków. Drużyny sportowe częściej składają się z nieparzystej niż parzystej liczby zawodników. Tenisiści zmieniają strony kortu, gdy suma rozegranych gemów jest nieparzysta - a to dlatego, żeby być serwującym i odbierającym raz po jednej, raz po drugiej stronie kortu.

Obserwacje, kalkulacje

Przez dwadzieścia lat na pierwszym wykładzie dla kilkudziesięcioosobowej grupy studenckiej rozdawałem karteczki i dawałem jedno polecenie: proszę napisać dowolną liczbę naturalną między 1 a 100. Trzy sekundy czasu. Już. Aha: i proszę dopisać swoją płeć (M, K). Zawsze, ale to zawsze znaczna większość studentów wybierała liczbę nieparzystą (60-80%). Ponadto - i to dopiero ciekawe - procent osób wybierających liczbę nieparzystą był większy u dziewcząt. Właściwie powinienem to opublikować jako ciekawostkę psychologiczną.

1. Przedstawienie liczby 1 w postaci ułamków o nieparzystych mianownikach.

Szachownica do gry w szachy ma 64 pola. Połowa z nich to białe, druga połowa - czarne. Na czarnych klawiszach gramy w warcaby. W tej grze pionki poruszają się po ukośnych rzędach. Zaznaczę ukośne rzędy kolorami - otrzymam ładny ornament (2).

2. Ładny ornament…

3. …zamieniony w "przyrząd" do serii obserwacji.

Wstawię tam liczby (3). Na bokach jedynki, a poza tym każda liczba będzie sumą trzech z poprzedniego rzędu, stojących nad nią (z wyjątkiem tych które, z braku trzeciej, są sumą dwóch). Przypomina to trochę trójkąt Pascala, z zasadą, że każda liczba jest sumą dwóch stojących nad nią). Wykorzystajmy to do serii obserwacji i wyłaniających się stąd ciekawych zadań.

1+1+1=3

1+2+3+2+1=9=3²

1+3+6+7+6+3+1=27=3³

1+4+10+16+19+16+10+4+1=81=3⁴

1+5+15+30+45+51+45+30+15+5+1=243=3⁵

1+6+21+50+90+126+141+126+90+50+21+6+1=729=3⁶

1+7+28+77+161+266+357+393+357+266+161+77+28+7+1=2187=3⁷

i tak dalej…

Po drobnej zmianie mamy:

1–1+1=1

1–2+3–2+1=1

1–3+6–7+6–3+1=1

1–4+10–16+19–16+10–4+1=1

1–5+15–30+45–51+45–30+15–5+1=1

I tak dalej. Zawsze dostaniemy 1.

Lubię posługiwać się arkuszem kalkulacyjnym - narzędziem nieobecnym w mojej młodości, a nawet w średnim wieku (Czytelniku: to ile ja mogę mieć lat?). W arkuszu kalkulacyjnym mamy wyciągniętą na wierzch zasadę działania komputera: przesyłanie wartości z jednych komórek do drugich. Widzimy ekran pokratkowany jak kartkę "zeszytu do matematyki" (a więc w kratkę, w odróżnieniu od zeszytu do polskiego - w linię). Zeszyt … niegdyś święty przedmiot szkolny, dziś traktowany z pewnym lekceważeniem.

4, 5. Czy odczytasz tu dowód wzoru 1 + 3 + 5 + 7 + … + (2n−1) = n²?

W arkuszu kalkulacyjnym przesyłamy wartości liczb, sami bądź "automatycznie": podstawowe funkcje matematyczne i możliwości samego arkusza są skondensowane pod postacią różnych ikonek. Wystarczy kliknąć…

"Wystarczy kliknąć" - zaklęcie XXI wieku. Z przyjemnością usiadłem w ogródku z laptopem i pobawiłem się zależnościami między pokazywanymi liczbami. A zatem "rozwiązałem" takie zadania. Słowo "rozwiązanie" musi być w cudzysłowie. Arkusz kalkulacyjny nie daje dowodu zgodnego z matematycznymi wymaganiami ścisłości. Dowód matematyczny to wyprowadzenie tezy z założeń za pomocą reguł logiki. Żadnych odstępstw.

Zadanie 1. Wykaż, że suma wyrazów w poziomych rzędach jest potęgą trójki, a suma naprzemienna tych wyrazów jest równa 1.

Zadanie 2. Wykaż, że jeżeli p jest liczbą pierwszą, to wszystkie liczby wiersza o numerze p, z wyjątkiem środkowego, są podzielne przez p.

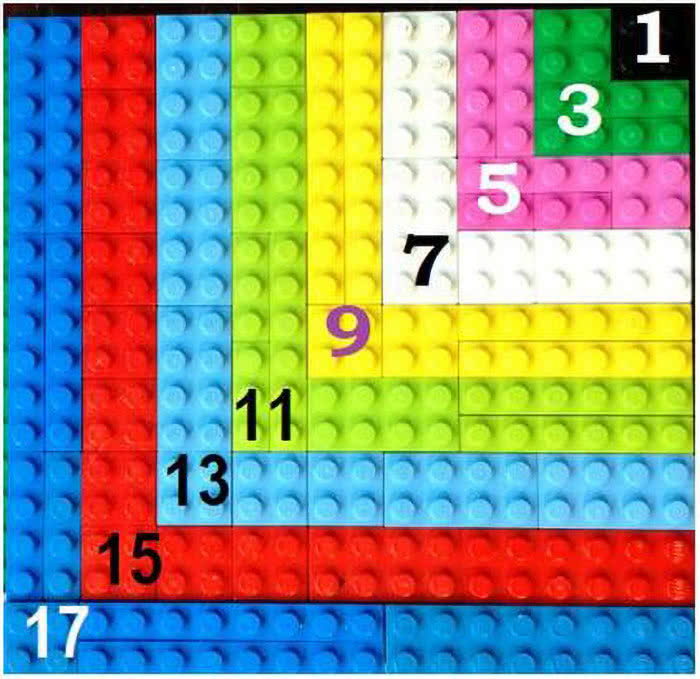
Zadanie 3. Wykaż, że jeżeli ciąg składa się z kolejnych liczb nieparzystych, a więc 1, 3, 5, 7, 9, 11, i tak dalej aż do 2n-1, to jego sumą jest n².

Zadanie 4. Popatrz na ilustrację 4 oraz 5 i z każdej z nich odczytaj "dowód" wzoru 1+3+5+7+…+(2n−1)=n².

6. Prostokątna spirala Archimedesa. Długość łamanej od punktu środkowego do końców poszczególnych boków to kolejne kwadraty liczb nieparzystych.

Najładniejsza jest ostatnia fotografia (7). Widzimy na niej siatkę trójkątów, pogrupowanych w łańcuchy po 1, 3, 5, 7, … trójkątów. A skąd wiemy, że wszystkich trójkątów jest n²? Z … geografii. Mapa w skali 1 do n zmniejsza długości odcinków n-krotnie, ale obszary (pola) n²-krotnie. Inaczej mówiąc, pola figur podobnych są proporcjonalne do kwadratu długości odpowiednich boków, a zatem duży trójkąt ma n² małych. Proste, a pomysłowe!

7. Siatka trójkątów pogrupowanych w łańcuchy

Dojść do grani

Liczby parzyste i nieparzyste wracają mi we wspomnieniach… z dzieciństwa. Odkryłem samodzielnie, że suma liczb parzystych jest parzysta, dwóch nieparzystych - też. Dalej, że mnożenie liczb parzystych da liczbę "jeszcze bardziej parzystą". Pomyślałem, że wobec tego iloczyn liczb nieparzystych winien być "jeszcze bardziej nieparzysty". Nie umiałem tego sformułować.

Moich problemów nie rozumiała nauczycielka, skądinąd bardzo dobra. Po latach umiałem to docenić. Gdy byłem już studentem, zrozumiałem, że owe moje odkrycia arytmetyczne to coś, co w kursie algebry abstrakcyjnej nazywane jest Pierwszym Twierdzeniem o Homomorfizmie. Co to jest? Ach, to proste. Przy homomorfizmie pierścieni obraz podzielony przez jądro jest izomorficzny z obrazem.

Nie żartuję sobie z Czytelnika, że to proste. Wymaga tylko… dużego przygotowania. Odwołam się do realiów tatrzańskich. Wycieczka granią Orlej Perci (w każdym razie od Zawratu do Granatów) nie jest specjalnie trudna. Tyle że najpierw trzeba się "tam" dostać. Polecam młodzieży - tak, jak polecam matematykę, wciąż Królową Nauk. No cóż, zdaję sobie sprawę, że w dzisiejszym świecie król może i panuje, ale nie rządzi. Z matematyką jest chyba odwrotnie: rządzi, ale nie panuje.

Trwają dyskusje o nauczaniu, o szkole, studiach, o kształceniu. Może matematyka przestała by być zmorą uczniów, gdyby… rozdziały podręczników przypominały ten mój artykuł? A jeśli przestałaby być takim straszakiem, to… co by ją zastąpiło?