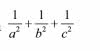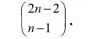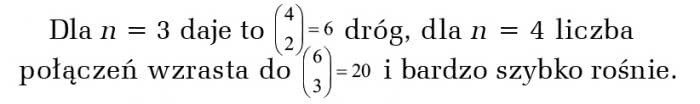Szachownica i szachy

Gra w szachy zanika jako rozrywka towarzyska, ale dobrze się ma jako sport. Od poprzedniego roku szkolnego znajduje się w programie nauczania zwykłych szkół podstawowych (!) - na razie w kilkunastu pilotażowych placówkach oświatowych i jest tam traktowana serio, jako jeden z przedmiotów. Inicjatywie tej należy przyklasnąć z entuzjazmem. Wołamy przecież, by uczyć dzieci myślenia. Matematyka jest do tego najlepsza, to prawda - ale nie jedyna i nawet nie powinna być jedyna. Praktyki monopolistyczne nie wychodzą nikomu na dobre.

1. Klasyczna szachownica 8 na 8. Zgodnie z regułami gry w tej wersji, po prawej u dołu znajduje się białe pole.

To zachęciło mnie do kolejnego powrotu do matematyki związanej z pokratkowaną i pokolorowaną kwadratową deską. Kolejnego - bo wiele lat temu pisałem o tym w "Rozmaitościach matematycznych". Postaram się jak najmniej powtarzać stare tematy, choć to było naprawdę dawno, w poprzednim tysiącleciu i dla innego pokolenia Czytelników. Wtedy jeszcze wierzono, że komputer nie pokona człowieka.

A więc kilka odcinków obecnych "Rozmaitości matematycznych" będzie o szachach, choć tak naprawdę sama gra w szachy wystąpi jako tło. Interesuje mnie ciekawa matematyka, jaka za tym stoi.

Nazwę "zadaniem" takie oto polecenie:

Zadanie 1. Przypomnij sobie, jak koduje się pola szachownicy, nazwy figur, bicie i groźny szach. Najbardziej klasycznym otwarciem gry jest 1.e2-e4 e7-e5. Wykonaj te ruchy albo tylko je sobie wyobraź.

2. Ruch konika szachowego - z czerwonego punktu konik może skoczyć na jedno z niebieskich.

Zadanie 2. (łatwe, bez odpowiedzi). Jeśli utrzymamy regułę, by białe pole było po prawej u dołu, to których pól jest więcej na nieparzystopolowej szachownicy: białych, czy czarnych? O ile więcej?

Zadanie 3. Na pewno wiesz, jak porusza się konik szachowy: po literze L albo Γ. Inaczej: z zajmowanego pola może skoczyć na pole znajdujące się w "odległości" (1, 2) albo (2, 1) - to znaczy jedno pole w danym kierunku, a dwa w drugim, prostopadłym. Matematycznie można to ująć w następujący sposób: nowe położenie to stare plus jeden z wektorów [1, 2], [–1, 2], [1, –2], [–1, –2], [2, 1], [2, –1], [–2, 1], [–2, –1]. Jeśli nie wiesz, co to wektor, spójrz w ten sposób: skok o wektor [1, 2] to po prostu skok o jedną kratkę w prawo i dwie do góry. Oczywiście domyślasz się, że [–1, 2] to skok w lewo o jeden i dwa w górę, a [–1, –2] znaczy "jeden w lewo, dwa w dół". Z każdego punktu szachownicy, nieleżącego zbyt blisko jej brzegu, możemy więc skoczyć na osiem pól. Możliwe położenia tworzą ładny ośmiokąt, niestety nie jest on foremny (rys. 2).

3. Droga konika (skoczka) na szachownicy 25-polowej.

Wykaż, że na szachownicy 8 na 8 konik może dostać się z każdego pola do każdego innego. Jak ma się dostać z jednego narożnika do przeciwnego? A z pola na pole sąsiadujące? Spójrz teraz na rys. 3. Jest na nim droga konika szachowego na szachownicy 25-polowej: wykorzystane jest każde pole. Znajdź w Internecie diagramy konikowe na szachownicy 8 na 8. Niektóre są bardzo estetyczne.

Zadanie 4. Wykaż, że na szachownicy o rozmiarach 5 na 5 nie istnieje zamknięta droga konikowa, to znaczy taka, by z ostatniego pola można było z powrotem przeskoczyć na pierwsze. Wskazówka: konik przy każdym skoku zmienia kolor pola.

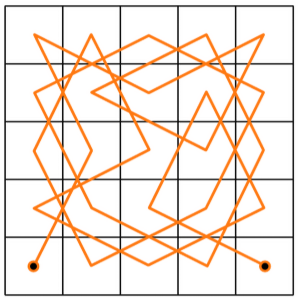
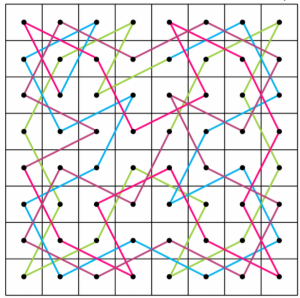
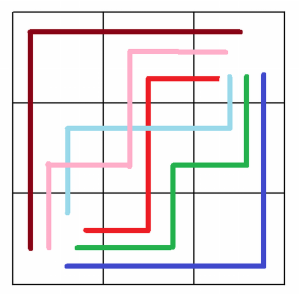
Pokażę jedną z metod konstrukcji zamkniętej drogi konika (skoczka) na szachownicy 8 na 8. Jest takich metod wiele. Jedną z najprostszych podał angielski lekarz, filolog i matematyk- amator Peter Mark Roget (1779-1869). Dzielimy szachownicę na cztery kwadraty, w których wpisujemy litery a, b, c, d - w porządku takim, jak na rys. 4. Zaczynamy od prawie dowolnego pola (są pewne ograniczenia), np. od pola oznaczonego dużą literą A. Skaczemy po literze a najpierw w lewym kwadracie, potem po prawym górnym, potem prawym dolnym i lewym dolnym. Po szesnastu ruchach przeskakujemy na literę b - zmieniamy kolor linii z czerwonego na fioletowy (rys. 5), potem przechodzimy na literę c (linia zielona) i kończymy skokami po d - linia niebieska.

Dominacja królowych

4. Zasada konstrukcji zamkniętej drogi konikowej na szachownicy 8 na 8.

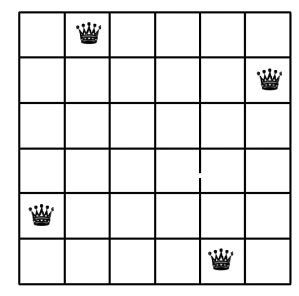
Od wielu lat nauczam algebry liniowej w niepaństwowej szkole wyższej. Studenci mają tam kłopot z kilkoma pojęciami, w tym "generowanie" i "niezależność". Spójrzmy na rys. 5 i 6. Widzimy tam królowe (hetmany) ustawione w charakterystyczny sposób. Każde pole szachownicy jest atakowane przez co najmniej jedną królową. Mniej królowych nie da się wziąć. Matematycznie: jest to minimalny układ generujący.

Zadanie 5. Ile królowych trzeba do tak rozumianej "kontroli" szachownicy 8 na 8? Nie podam odpowiedzi. Jest ona na stronie www.flyordie.com/chess/queendomination - można tam też efektywnie próbować własnych ustawień (strona podpowiada rozwiązania).

Zadanie 6, licealne. Wykorzystam szachy do zadania, które teoretycznie jest na poziomie licealnym, a praktycznie może je rozwiązać każdy. Na ile sposobów da się przejść od lewego dolnego narożnika do prawego górnego, zakładając, że poruszamy się po jednym polu wzdłuż pasa pionowego albo poziomego? Skok po przekątnej - tak jak królem szachowym - nie jest dozwolony.

5. Jedna z metod konstrukcji zamkniętej drogi konika na szachownicy 8 na 8.

Podam rozwiązanie. Najpierw jednak komentarze.

Matura, w obecnej postaci, spełnia swoje zadanie. Dobrze sprawdza umiejętności młodzieży. Idealnego systemu jednak nie ma. Dużą wadą obecnego sposobu egzaminowania jest to, że narzuca taki schemat, iż po otrzymaniu zadania uczniowie i studenci natychmiast szukają wzoru, do którego można podstawić dane, by po pewnych rachunkach otrzymać wynik. Gorzej - dziwią się nawet, że są zadania innego typu, a mianowicie typu "najpierw pomyśl!" albo "skorzystaj najpierw z jednego wzoru, a potem z drugiego". Bardzo źle jest z "czytaniem ze zrozumieniem".

W dwóch równoległych grupach dałem kiedyś w gruncie rzeczy to samo zadanie.

W jednej było: "Dane są liczby: 2, 3 oraz 5. Oblicz sumę odwrotności ich kwadratów".

W drugiej: "Oblicz wartość wyrażenia

dla a = 2, b = 3, c = 5".

5. Cztery królowe chronią każde pole szachownicy 6 na 6, to znaczy, że każde pole (z wyjątkiem tych, na których same stoją) jest szachowane przez którąś. Żadna nie szachuje innej - matematycznie znaczy to, że układ jest niezależny.

Większość (!) studentów pierwszej grupy "poległa" na analizie semantycznej zbitki "suma odwrotności kwadratów". Z kolei prawie wszyscy studenci drugiej grupy zrobili zadanie poprawnie, choć niektórzy mieli kłopoty z dodawaniem ułamków.

Zadanie 8. No, to ile jest równa "suma kwadratów odwrotności"? A odwrotność sumy kwadratów? A kwadrat odwrotności sumy? Może to to samo?

Zadanie 9. - też nie na temat szachowy, ale kiedyś dałem je do rozwiązania na kolokwium i studenci potem zapowiadali mi, że napiszą skargę do dziekana, iż uprawiam "mobbing": sadystycznie dręczę ich okropnymi zadaniami. Brzmiało tak: "Oblicz iloczyn kolejnych liczb całkowitych od -111 do +178". Muszę przyznać, że gdy zrozumieli, o co chodzi, śmieli się z samych siebie.

Wracam do zadania 6. Podróżujemy z południowego zachodu na północny wschód. Dobierzmy wędrownikowi towarzysza. Wyobraźmy sobie, że dwa narożniki to dwie miejscowości podgórskie w niewysokich, trawiastych górach, pokrytych pastwiskami tak, że ścieżki prowadzą tylko w kierunku wschód-zachód lub północ-południe. Przekątna kwadratu to wysoki grzbiet. Musimy wejść na niego i potem z niego zejść.

6. Na szachownicy 11 na 11 potrzeba pięciu królowych. Zaznaczone są pola atakowane przez jedną królową (zielone), dwie (żółte) i trzy (czerwone).

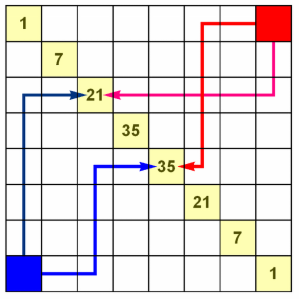
Ile jest dróg z niebieskiego kwadratu (rys. 7) do północno-wschodniego punktu na grani? Oczywiście jedna: za każdym razem na północ. Zakodujemy ją jako 1111111 (siedem jedynek). Będziemy pisać 0 na zaznaczenie, że wybieramy drogę na wschód ("poziomo w prawo"). Wtedy dwie drogi wychodzące z południowo-zachodniego narożnika to 0011100 oraz 1111100. Takie układy zer i jedynek odpowiadają liczbom dziesiątkowym 4 + 8 + 16 = 28 oraz 4 + 8 + 16 + 32 + 64 + 128 = 252.

Liczby na przekątnej ("na grani") pokazują, na ile sposobów można się dostać z narożnika na grań. To wynika od razu z trójkąta Pascala (wiadomości licealne nawet na poziomie podstawowym). Wyobraźmy sobie, że dwóch turystów, z których jeden mieszka w miejscowości "niebieskiej", a drugi w "czerwonej", umówiło się na spotkanie w wyznaczonym miejscu grani. Mają taką samą kondycję, idą tak samo szybko, więc powiedzieli sobie przez telefon, że każdy wyjdzie o dziewiątej i ewentualnie poczekają na siebie na grani kilka czy kilkanaście minut.

Jeżeli umówili się w jednym z punktów "35", to każdy ma 35 sposobów dojścia. Po połączeniu daje to 35² możliwości drogi niebieski-czerwony. Tak jest dla każdego innego punktu spotkania. Łącznie możliwości jest zatem 1² + 7² + 21² + 35² + 35² + 21² + 7² + 1² = 3432.

Bardziej wprawni Czytelnicy mogą obliczyć, że gdy szachownica jest rozmiaru n na n, to dróg takich jest

Dla n = 3 daje to 4

7. Droga od niebieskiego kwadratu do czerwonego rozpada się na dwie części - z narożnika do "grani" (przekątnej) i zejścia do drugiego narożnika.

Dla n = 10 jest to już 48320. Taki wzrost nazywa się wykładniczy. Przypomina lawinę, która im szybciej spada, tym szybciej zwiększa swoją objętość i zwielokrotnia siłę niszczycielską.

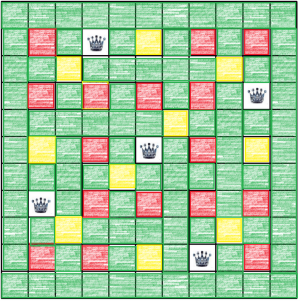
Zadanie 10. Wykorzystując szachownicę, wykaż, że suma kolejnych liczb nieparzystych jest kwadratem liczby naturalnej.

Szkic rozwiązania. Spójrzmy na rys. 1. Zliczamy czarne pola, od a1 poczynając i grupując w ukośnych rzędach: najpierw a1, potem a3 b2 c1, następnie a5 b4 c3 d2 e1, potem od a7 w prawo w dół.

Po północno-wschodniej stronie szachownicy wykonujemy to samo, a następnie robimy tak samo z polami białymi.

Szachy a podstawy matematyki

Wykorzystam teraz szachy i na ich przykładzie wyjaśnię pewną osobliwość dociekań matematycznych. Odkrycie tej osobliwości (Kurt Gödel, 1938, późniejsze uzupełnienie - Paul Cohen, 1963) wstrząsnęło podstawami matematyki. Generalnie rzecz biorąc, chodziło o istnienie bądź nieistnienie pewnych rodzajów nieskończoności. Łatwo bowiem wykazać, że np. nieskończoność, którą daje ciąg 1, 2, 3, 4, 5, 6, …. , jest inna niż ta, którą tworzą wszystkie liczby rzeczywiste: dodatnie, ujemne, ułamki (liczby wymierne) i niewymierne. U progu XX wieku niekwestionowany lider ówczesnej matematyki, David Hilbert (1862-1943), sformułował 23 problemy dla matematyków XX wieku. Numerem jeden było pytanie, czy między wymienionymi nieskończonościami jest jeszcze inna, różna od obydwu?

8. Sześć różnych dróg łączących narożnik południowo-zachodni z północno-wschodnim. Zauważmy, że cztery z nich (a więc dwie trzecie) przechodzą przez środkowy kwadrat.

Pytanie, jak pytanie. Zadanie do rozwiązania. Albo tak, albo nie. Albo taka nieskończoność jest, albo jej nie ma, prawda? Czy może być inaczej?

Może! To właśnie wykazał Kurt Gödel. Ani tak, ani nie! Posłużę się właśnie szachami. Spójrzmy na rys. 9. Widzimy tu pewne ustawienie figur na szachownicy.

Grajmy dalej, zobaczymy, kto wygra.

Wydaje się, że białe mają druzgocącą przewagę. Ruch jest oczywiście po stronie czarnych, bo czarny król jest szachowany. Jedynym ratunkiem jest bicie szachującego pionka przez królową, którą natychmiast bije biały goniec z pola g3. Wprawdzie czarny król ratuje się jeszcze, zabijając dzielnego gońca, ale wtedy biały pionek, chroniony przez wieżę z tyłu, wkracza na pole d8, zmienia się w królową i jest mat!

Rozumowanie jest w porządku. Chodzi jednak o to, że takie ustawienie figur nie może się zdarzyć w rzeczywistej partii, nawet najdziwaczniej prowadzonej przez graczy.

Po pierwsze, białe mają pięć gońców. Samo w sobie nie jest to sprzeczne z zasadami, bo trzy pionki mogły dojść do ósmego pasa, a grający białymi zdecydował, że chce je zmienić w gońce. Ale bardziej wnikliwa analiza pokazuje, że mogły to zrobić tylko pionki z kolumn a oraz b. Pionki z kolumn c, d, h stoją bowiem jeszcze na szachownicy, a czarny szereg pionków po prawej stronie u góry nie mógł być sforsowany przez białe. Dodatkowo, czarny goniec nie mógł znaleźć się w prawym górnym rogu (bo nie mógł przeskoczyć przez czarne pionki). Można zatem powiedzieć, że ta pozycja nie należy do gry w szachy. Nie da się do niej dojść przy normalnych regułach gry.

9. Pozycja niemożliwa

Tak samo bywa (ku zaskoczeniu samych matematyków) w matematyce. Na tym właśnie polegało odkrycie Kurta Gödla sprzed dokładnie osiemdziesięciu lat. Wykazał on, że istnieją takie zdania (stwierdzenia), które należą do matematyki (nawet: do arytmetyki), a których nie można udowodnić, ale nie można też wykazać, że są fałszywe.

Innym porównaniem, dzięki któremu można to zrozumieć, jest odniesienie do literatury.

Który numer buta nosił Henryk Sienkiewicz? Nie wiemy, ale może to odkryjemy, bo a nuż zachowały się księgi jakiegoś sklepu, gdzie zostało zapisane: "Pan Henryk Sienkiewicz kupił u nas dla siebie czarne buty nr 43". Mało prawdopodobne, ale tak czy owak, któryś numer buta miał. A który numer nosił Sherlock Holmes? Tu już możemy przyjąć prawie dowolną odpowiedź i żadna nie będzie odpowiadała rzeczywistości, bo rzeczywistości nie ma! Jest tylko fikcja literacka.

- No dobrze - powie Czytelnik. - Ale jak to jest z tą nieskończonością? Umiemy, czy nie umiemy udowodnić, ale jak jest naprawdę, w realnym świecie?

Odpowiedź rozczarowuje: nie ma "naprawdę".

Matematyka nie jest nauką przyrodniczą, nie bada świata za oknem - bada swój własny, wymyślony świat. A że on dobrze pasuje do rzeczywistości? Sami matematycy się dziwią.

Następna, poważniejsza już obawa Czytelnika może być taka: czy ja mam wobec tego wierzyć matematyce? I tu uspokoję wszystkich: w zakresie każdych obliczeń inżynierskich, gospodarczych, finansowych i wszystkich "ziemskich" matematyka jest jedna i pewna, choć nie nadaje się do nauk, w których ścisłość nie stanowi podstawowej cechy: filologii, psychologii, filozofii i historii. Owszem, znaczenie ma statystyka opisowa. Prawie nic innego. I bardzo dobrze.

Takie zadania, o jakich dzisiaj pisałem, wydają się klasycznymi łamigłówkami bez praktycznych zastosowań. Co komu z tego, ile królowych da się rozstawić na szachownicy? Być może rzeczywiście nic, ale chyba wszyscy lubimy łamigłówki.

Po drugie, co ważniejsze, zadania takie pochodzą od istotnych zadań współczesnej matematyki: co zrobić, żeby "coś" (= komputer) działało sprawnie, żeby wyszukiwarki były coraz lepsze, a pomiary dokładniejsze? Słowem: optymalizacja, potrzebna przecież na każdym kroku.

Michał Szurek