Pożytki z koronawirusa
Opiszę kilka swoich refleksji o nauczaniu zdalnym. Jest to namiastka i ersatz prawdziwego. Szczególnie boleśnie odczuły to młodsze dzieci. Mimo wysiłków pedagogów z tytułami naukowymi, od czasów Sokratesa (499 - 399 p.n.e) niewiele zmieniło się w dydaktyce. Kontakt mistrz-uczeń pozostaje niezastąpiony. Ale dobrze prowadzony wykład matematyczny dla licealistów i studentów może udać się nawet lepiej niż tradycyjny (złośliwe określenie: wykład akademicki jest taką formą przekazywania wiedzy, gdzie notatki profesora przechodzą do zeszytów studenckich z pominięciem świadomości obu zainteresowanych stron).
Ja wszyscy wiemy, w Internecie jest bardzo dużo dobrych i bardzo dobrych (i także dużo złych i totalnie bzdurnych) materiałów na praktycznie każdy temat. Obejrzałem kilkanaście z zakresu moich obecnych wykładów dla studentów informatyki. Znalazłem kilka wyśmienitych lekcji. Trudne pojęcia, nad którymi ślęczałem przed pół wiekiem, czytając linijka po linijce zwięzłe podręczniki akademickie, młodzi wykładowcy objaśniają teraz prosto, zrozumiale, nie tracąc głębi. Z racji przeżycia szkoły w PRL umiem trochę po rosyjsku. Strony rosyjskie są bardzo dobre. Coś niesamowitego. Amerykańskie też ujdą.
Zmuszony byłem i ja nauczać inaczej. Podchodziłem do tego "jak pies do jeża", ale dziekan mnie trochę przymusił. Musiałem się przestawić z akroamatycznej formy zajęć na … taką która może i nie ma nazwy - chodzi po prostu o to, żeby było dobrze. Nawet nie będę wyjaśniał, co to znaczy forma akroamatyczna. Sama nazwa odstrasza. Mogłem wykorzystać to, co "informatyka dała" - a zwracam uwagę, że urodziłem się jeszcze w pierwszej połowie "tamtego" wieku.
W katedrze uniwersyteckiej, w której pracowałem przez blisko 50 lat, część kolegów zajmowała się działaniami grup - bardzo interesującą dziedziną na pograniczu geometrii i algebry. Bardzo trudna i abstrakcyjna. Jeden z kolegów pracował kilkanaście lat nad praktycznie jednym zadaniem. W końcu rozwiązał, zresztą w "bardzo międzynarodowej" współpracy: Niemiec z obywatelstwem kanadyjskim Rosjanie żydowskiego pochodzenia z paszportami izraelskimi i amerykańskimi. Zawsze "bolało" mnie to, że swoich badań nie mogę przedstawić przeciętnemu Czytelnikowi (albo słuchaczowi) - zbyt były abstrakcyjne.
Okazało się, że po pewnych, może i dość znacznych uproszczeniach, mogę o tych problemach opowiadać nawet dzieciom - a w każdym razie studentom, którzy wcale nie byli "dobrzy z matematyki". Wymagało to kolosalnego przygotowania. Proszę mi wierzyć, że tradycyjne wykłady uniwersyteckie jest łatwiej prowadzić niż lekcje w szkole podstawowej.
No, to spróbujmy. Artykuł jest streszczeniem "zdalnego" wykładu dla studentów informatyki.
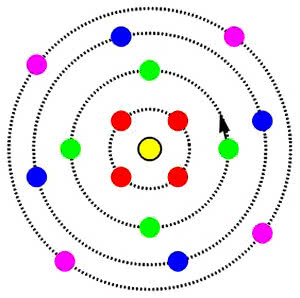
Zacznę od grupy przesunięć. To prosty algorytm. "Bierzemy i przesuwamy" (1). Czy ktoś z Państwa ma taki szlaczek na podłodze, albo w kafelkach w kuchni czy w łazience? Pojedynczy element nie powinien mieć żadnej symetrii. Pewnie nie, bo wolimy symetrię, choćby jak na rys. 2.
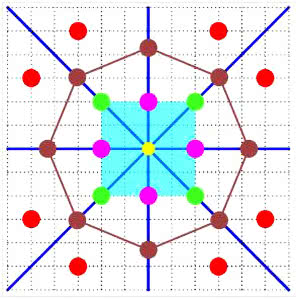
Nie trzeba wielkiej spostrzegawczości, by zobaczyć, czym różnią się kwadraciki na rys. 3. Można powiedzieć, że powstają przez obrót pierwszego z nich o 90 stopni w prawo, a potem jeszcze raz i jeszcze raz. Po czterech obrotach przywracane jest położenie wyjściowe. Matematyk powie, że działa tu grupa Z4. Tworzą ją cztery liczby: 0, 1, 2, 3, które dodajemy w ten sposób, że gdy suma przekracza 3, "obcinamy ją", i tak 2 + 3 to nie 5, a 1, zaś 4 +4 to nie 8, tylko 3. Czy to jest dziwne i nienaturalne?
A jak dodajemy godziny na zegarze (12-godzinnym). Każdy wie, że 8 + 6 = 2. Jak to? A no, jeżeli od ósmej upłynie sześć godzin, to zrobi się druga. To rozumiemy bardzo dobrze. Podobnie dodajemy obroty. Jeżeli kółko zębate ma 24 ząbki, to wykonanie najpierw obrotu o 15 , a potem o 13 ząbków da ten sam wynik, co obrót o 4. Ma to - jak cała matematyka - ograniczoną stosowalność. Spróbujmy obrócić się o 7290 stopni.
Zakręci nam się w głowie, ale "matematycznie" jest to tym samym, co znany żołnierzom "w prawo zwrot", albo "w lewo zwrot". Szeregowcy i generałowie wiedzą, że mają obrócić się o kąt prosty. Należy docenić, że w wojsku polskim "w tył zwrot" robi się przez lewe ramię. Obrót w lewą stronę matematycy nazywają dodatnim. Jesteśmy tego nieświadomie uczeni w szkole. A tak, tak - przypomnijmy sobie, jak oznaczymy wierzchołki trójkąta.
Na pewno każdy wpisze A, B, C tak, że A będzie po lewej, B po prawej, a C na górze - a zatem kierując się w lewo - przeciwnie do ruchu wskazówek zegara.
Na pytanie, dlaczego matematycy chcą, by obrót dodatni był przeciw wskazówkom zegara? Mam na to nie do końca poważną odpowiedź: matematyka pojawiła się na długo przed wynalezieniem zegara. Jako pierwsi, mieliśmy wolny wybór. Ale wracajmy do głównego wątku.
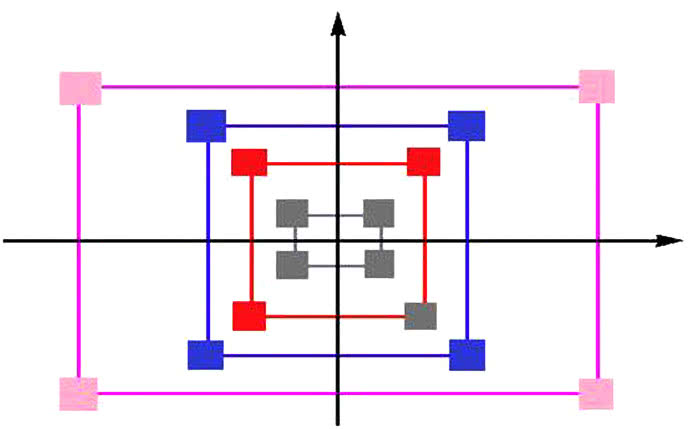
Duże znaczenie ma w matematyce niepozorna grupa symetrii prostokąta, zwana też grupą Kleina Kilka słów o tym matematyku niemieckim (Felix Klein, 1849 - 1925). Jego program z Erlangen, zmienił topos pojmowania geometrii przez samych matematyków. Według tego programu geometria jest badaniem grup przekształceń. Nie mogę rozwijać tego tematu teraz - wymagało by to osobnego omówienia. Spójrzmy na rys. 5. Jak zmienia się kolorowy (zielono-żółto-czerwono-niebieski) prostokąt? W kierunkach poziomym i pionowym mamy symetrie. Po przekątnej - obrót o 180 stopni, albo (bo to jest to samo) symetrię środkową.
Kwadrat, to taka dziwna figura,
Bo nie wiadomo, gdzie dół, a gdzie góra.
Tak samo długi, jak i szeroki.
Ma równe kąty i równe boki.
Okrąg wpisany i opisany,
Mają w nim ten sam środek podany.
Cztery symetrie i cztery obroty!
Mamy z kwadratem co do roboty.
Zadanie (nie tylko dla studentów). Podaj przykłady działania grupy Z2, czyli grupy złożonej z dwóch elementów. O co tu chodzi? Zero i jeden. Włącz-wyłącz. Mąż i żona. Sherlock Holmes i dr Watson. Jeremi Przybora i Jerzy Wasowski. Mecz piłkarski ("my" - "oni"). Lewo i prawo. Prawda i fałsz. Zło i dobro; diabeł i anioł. Przeciwieństwa, które nie mogą istnieć bez siebie.
O wykorzystaniu działania grupy Z2 w konstrukcji niemieckiej maszyny Enigma pisałem kilka miesięcy temu (w wersji dla studentów było: mówiłem na poprzednim wykładzie). Istotą metody była symetria liter, zmieniana co chwila. Bez tej zmienności rozbicie szyfru by było bardzo proste. Jak pamiętamy, największe zasługi w poznaniu tajemnicy Enigmy mieli polscy kryptolodzy: Marian Rejewski, Jerzy Różycki i Henryk Zygalski. Wykorzystamy pomysł "zmiennej symetrii" do … układania tabeli rozgrywek ligi piłkarskiej (czułem zdalnie, że studenci się ożywili, przynajmniej chłopcy).
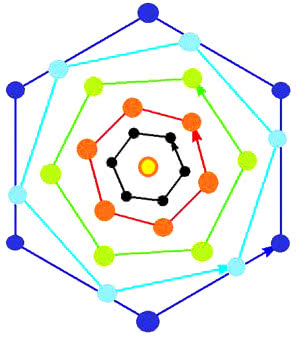
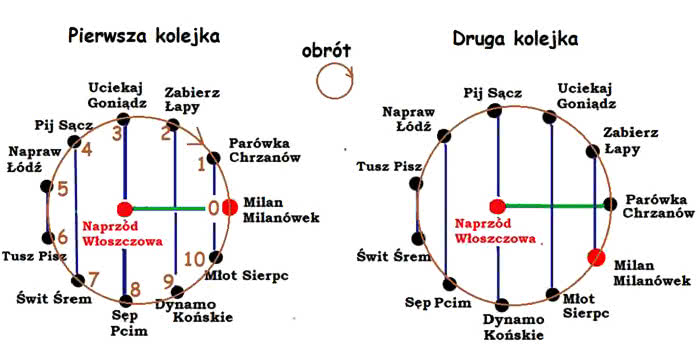
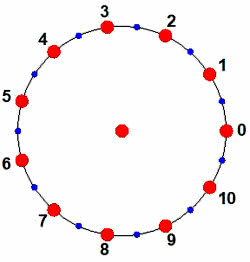
Wyobraźmy sobie, że w rozgrywkach bierze udział 12 drużyn z miejscowości: Chrzanów, Goniądz, Końskie, Łapy, Łódź, Milanówek, Pcim, Pisz, Sącz, Sierpc, Śrem i Włoszczowa. Przyjmijmy też, że mistrzem z poprzedniego roku jest sympatyczna drużyna Na przodu Włoszczowa. Ustawiamy ją w środku, a pozostałych jedenaście umieszczamy na kole (okręgu, rys. 9). Matematycznie wygodniej jest numerować od zera: drużyny od 0 do 11, a kolejki rozgrywek też od zera. W kolejce zerowej (otwierającej sezon) Naprzód gra z Milanem, a pozostałe pary wskazują pionowe linie. Można powiedzieć, że łączą one drużyny "symetryczne". Druga (mająca "matematyczny" numer 1) kolejka kojarzy Naprzód z Parówką Chrzanów - a pozostałe drużyny też według zasady symetrii (albo: po niebieskich pionowych liniach).
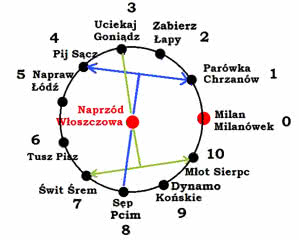
Możemy też kręcić kółkiem wewnętrznym (zależy, jak wytniemy). Wtedy nazwy drużyn pozostaną na miejscu, a obracać się będzie wzorek wewnętrzny. Pomaga to zrozumieć sposób wyznaczania, w której kolejce grają ze sobą dane drużyny. Prowadzimy przez te drużyny cięciwę koła. Symetralna tej cięciwy przechodzi przez środek koła, czyli przez Naprzód. Symetralna pokazuje, z kim gra w tej kolejce Naprzód. Numer przeciwnika Naprzodu jest numerem kolejki, w której spotykają się dane dwie drużyny. Na rysunku 10 widać, że Pij z Parówką gra w kolejce numer 8, a Młot ze Świtem w kolejce nr 3 (wtedy Naprzód gra z Uciekajem z Goniądza).
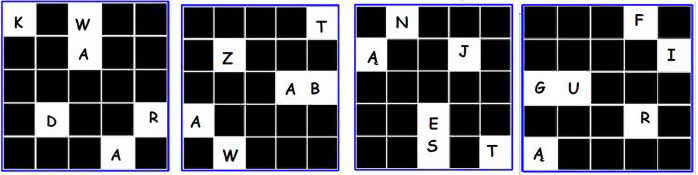
I jeszcze o grupie Z4, czyli o obrotach kwadratu (zob. też rys. 3). Zastosujemy ją do stworzenia szyfru - może niezbyt skomplikowanego, ale ciekawego. Z kwadratu o 25 oczkach wycinamy sześć. Jak? Zostawiam to Czytelnikom/studentom jako zadanie. Ja zrobiłem tak, jak na rysunku 12. Kodowany tekst wpisuję, litera po literze, w wolne pola. Następnie obracam moją "maszynę szyfrującą" o 90 stopni. Pojawiają się nowe wolne pola. Wpisuję. Obracam. Wpisuję. Obracam. I jeszcze raz. Zdejmuję siatkę. To, co otrzymałem, pokazuje rys. 13. Czy to dało by się "złamać"? A gdyby wziąć większy kwadrat albo inną figurę?
KNWFT ĄZAJI GUAB ADERR ĄWSAT
I jeszcze o kwadracie.
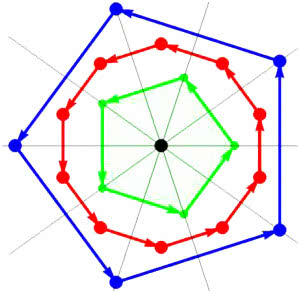
Co kojarzy się nam z grupą obrotów? Mam nadzieję, że uczniowie w szkole dowiadują się jeszcze o tym, kim był Mikołaj Kopernik. De revolutionibus orbium coelestium. O obrotach ciał niebieskich, 1543. "Wstrzymał Słońce, ruszył Ziemię, polskie go wydało plemię!". Na rysunku 4 mamy orbity punktów. Orbitą punktu przy działaniu grupy Z4 są pozostałe trzy punkty tego samego koloru (no i on sam). Żółty punkt w środku ma orbitę jednopunktową - złożoną z niego samego.
Zdalne nauczanie coraz bardziej lubię. Ale lepiej, żeby się skończyło.
Ale jeszcze jedna dygresja. Zawód informatyka znów zyska na znaczeniu. Z moich prywatnych obserwacji wynika, że wielkie korporacje i małe firmy zobaczyły, ile pracy można wykonywać zdalnie. A jakie oszczędności przy tym! Potrzeba mniej pomieszczeń, pracownicy siedzą we własnych domach, nierzadko pracują na własnym sprzęcie, piją własną kawę i brudzą u siebie.
Michał Szurek