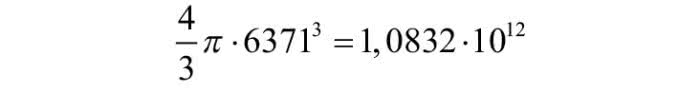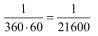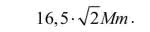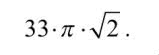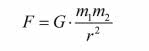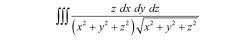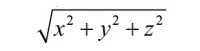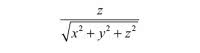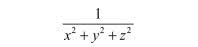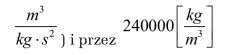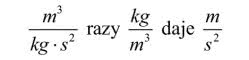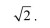Efekty zdalnej nauki, istniejące i nieistniejące planety

Internet straszy nas (w każdym razie mnie, mniej więcej raz na tydzień) końcem świata spowodowanym przez czyhającą już planetoidę, która rozłupie Ziemię. Bo proszę: 18 sierpnia minął Ziemię w odległości 3000 km tajemniczy podługowaty obiekt, nazwany Oumuamua. Miał kształt wydłużonego cygara o długości kilkunastu metrów. Gdyby był kilka tysięcy razy większy, miałby już własne pole grawitacyjne, bardzo ciekawe. Może żyłyby tam inteligentne istoty? Przyjrzyjmy się takim nietypowym światom. Ale zacznijmy skromnie, od płaskiej Ziemi. Wyliczmy matematycznie, jak to by na niej było. Profesorowie astronomii są zgodni - płaska planeta nie może istnieć. Nie ma prawa. Nie mogłaby powstać, a gdyby nawet, to własna siła grawitacji ścisnęłaby ją do kuli. Wyliczymy, jak to jest.

Matematycy jakoś nie bardzo przejmują się światem zewnętrznym i tylko dziwią się od czasu do czasu, że ich wydumane teorie nieźle sprawdzają się w świecie rzeczywistym. Odnotujmy, że w lutym 2020 roku zmarła w wieku 101 lat Katherine Johnson, matematyczka, która obliczała tory amerykańskich lotów kosmicznych, od lotu Johna Glenna w 1961 do lotów księżycowych. Obliczenia musiały oczywiście uwzględniać wiele trajektorii awaryjnych. Jak może Czytelnicy wiedzą, bardzo się to przydało w feralnej misji Apollo 13.

Zwróćmy uwagę, że pani Johnson miała - przynajmniej we wczesnych latach sześćdziesiątych - do dyspozycji tylko… suwak logarytmiczny, a moc obliczeniowa pierwszych komputerów zastosowanych w lotach księżycowych była mniejsza od możliwości dzisiejszych smartfonów. W zadaniach matematycznych Ziemia jest kulą o promieniu 6371 km. Pani Johnson musiała przyjąć dokładniejsze dane - pomyłka mogłaby spowodować, że astronauci wylądowaliby zamiast na Pacyfiku, to na przykład w Związku Radzieckim. Nie mówiąc o tym, że mogliby odlecieć w nieskończoność…

Po trzecie, Czytelnicy nie znają pewnie rosyjskiego barda, Jurija Kukina (1933-2011), popularnego i u nas w moich czasach studenckich. W jednej z jego piosenek występuje маленкий гном (malutki gnom). Na krytykę władz Związku Radzieckiego, że krasnoludków przecież nie ma, Kukin odparł: "przepraszam, to jak się nazywają te małe, leśne ludziki w śmiesznych czapeczkach?"

1. Planeta Placuszek. Jej rozmiary to a=33Mm, h=0,01 Mm

Tak czy owak, zabrałem się do studiowania życia na płaskiej planecie. Wniknięcie w takie światy umożliwia nam matematyka. Pamiętamy, że Ziemia, jaką znamy, jest głęboka na co najmniej kilkanaście kilometrów (Rów Filipiński). Dla uproszczenia obliczeń przyjąłem, że gdyby była płaska, miałaby grubość 10 km. Oczywiście musi być dostatecznie masywna, żeby wytworzyć ciążenie. Nazwałem tę planetę Placuszkiem (1). Dla tych z Czytelników, którzy już są zniecierpliwieni nierealnym tematem, proponuję, by po prostu traktowali to wszystko jako ćwiczenie matematyczne.

Matematyk lwowski, a od 1945 roku wrocławski, Hugo Steinhaus (1888-1972) jest autorem wielu "aforyzmów matematycznych", w tym takiego: "Kula u nogi? Ziemia!". Przyjrzyjmy się naszej kuli u nogi. W zadaniach matematycznych jest kulą o promieniu 6371 km (naprawdę jest nieco spłaszczona na biegunach i w ogóle trochę nieregularna). Ma objętość

kilometra sześciennego (czyli 1083 megametry sześcienne) i "waży" 5,9722·10²⁴ kg. Przypomnę, że metr sześcienny wody to 1000 kg, czyli tona. Obliczenia uproszczają się, a świat wygląda ciekawiej, gdy założę, że moja płaska planeta nie jest okrągłą pizzą, a kwadratową (takie robi moja żona, po prostu mamy blachę tego kształtu). Tak, tak, wiem, że powinienem napisać poprawnie: mój Placuszek jest prostopadłościanem o kwadratowej podstawie i wysokości h=0,01 Mm, jedna setna megametra.

Megametr to, jak pamiętamy, milion metrów, czyli 1000 km (1). Nad Placuszkiem świeci słońce, ale zwykłe, kuliste. Zauważmy, że na Placuszku nie ma stref czasowych. Wynurzające się spod horyzontu słońce oświetla od razu całą planetę.

Przyjmijmy, że powierzchnia Placuszka to kwadrat o boku a=33 Mm. To bardzo dużo, niemal jedna dwunasta odległości Ziemia-Księżyc! Planeta jest głęboka na 10 km. Był kiedyś projekt zrobienia przekopu na drugą stronę, ale jako skrajnie nonsensowny, ekonomicznie nieopłacalny i morderczy ekologicznie został szybko zarzucony, dzięki rozsądkowi Placuszkan - czyli istot zamieszkujących planetkę. Pozazdrościć. Nie było też przekopów międzyludzkich…Weźmy się jednak za objętość Placuszka. Jest ona oczywiście równa a²h=33²·0,01=10,89 Mm³.

Jeden megametr sześcienny to 109 kilometrów sześciennych. To znaczy, że objętość Placuszka wynosi 10,89·10⁹ kilometrów sześciennych. To bardzo ciekawe, bo to prawie dokładnie sto razy mniej niż objętość naszej Błękitnej Planety, Ziemi. Co za niesamowita zbieżność! Natomiast gęstość gruntu Placuszka jest - jak się okazuje - blisko pięćdziesiąt razy większa niż Ziemi i wynosi 240 gramów na centymetr sześcienny (Ziemia ma 5,515 g/cm³). Jest to bardzo dużo, ale dzięki temu Placuszek nie przełamuje się. Placuszek jest więc bardzo masywną planetą, 240 razy cięższą od Ziemi (Jowisz jest od Ziemi 317 razy cięższy).

Zadanie dla uczniów. Wyraź gęstość Placuszka w kilogramach na metr sześcienny.

Podaję rozwiązanie - mam w pamięci studentów, którzy uważali, że jeżeli metr ma 100 centymetrów, to metr sześcienny ma 100 centymetrów sześciennych. O dziwo, trafiał do nich niepedagogiczny argument: ile to jest "setka wódki?". Metr sześcienny to 100³=10⁶ (tak, milion!) centymetrów sześciennych. Metr sześcienny gruntu Placuszka ma więc masę 240·10⁶ gramów. Ponieważ tona to 10⁶ gramów (znów milion), zatem gęstość Placuszka to 240 ton na metr sześcienny. Zadanie rozwiązane. W obliczeniach posłużymy się jednak kilogramami, 240000 kilogramów na metr sześcienny. Jeszcze raz przypomnę, że jest to ponad pięćdziesiąt razy więcej niż na Ziemi, a Ziemia jest planetą o największej gęstości w całym Układzie Słonecznym (choć Merkury i Wenus mają tylko nieznacznie mniejszą).

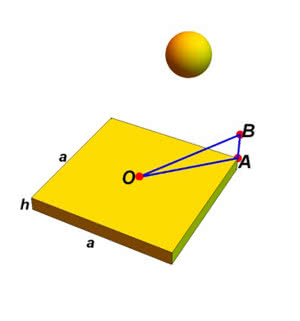
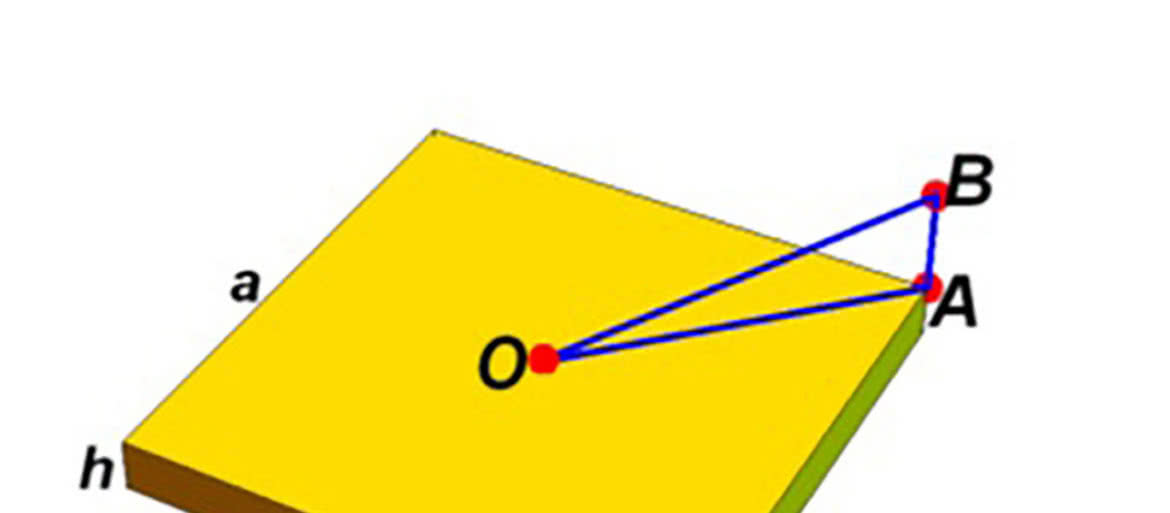
Stolicą Placuszka jest gród O. W najdalszych punktach ustawiono wieże tak wysokie, żeby z każdego punktu było widać choć jedną. I oto pierwsze zadanie. Jak wysokie są wieże?

Placuszkanie są pod wieloma względami podobni do ludzi (o różnicach będzie dalej). W szczególności mają podobny wzrok. Widzą tak dobrze, jak my. A jak my widzimy? Rozdzielczość ludzkiego oka szacowana jest na około jednej minuty kątowej. Co to znaczy? Wyjaśnię nie tyle przypowieścią, co na przykładzie prawdziwego zdarzenia. Pewnego razu leciałem samolotem z Warszawy do południowych Niemiec. W okolicach Rawy Mazowieckiej osiągnęliśmy już wysokość przelotową. Ku mojemu dużemu zdziwieniu, za oknem po lewej stronie zobaczyłem Tatry! Znam je z młodości dość dobrze i od razu rozpoznałem bardzo charakterystyczną grań, opadającą stromo, ale jednostajnie ze Świnicy na Przełęcz Świnicką. W linii prostej jest to tylko 700 metrów. Nie miałem żadnej wątpliwości, że to ta grań. Przyjmijmy, że dzieliło mnie od niej 350 km. Pod jakim kątem widzimy odcinek 750 metrów z odległości 350 km? Obliczenia zostawiam Czytelnikowi.

Odpowiedź: około 7 minut kątowych. Rozdzielczość mojego widzenia była wtedy 7 minut kątowych, a nawet znacznie mniejsza, bo rozpoznałbym i krótszy odcinek. Podobno w nader sprzyjających warunkach młody człowiek z dobrym wzrokiem może mieć rozdzielczość wzroku nawet jedną minutę kątową.

Uśmiecham się tutaj do jednego z moich wiernych czytelników ze Szczecina. On się domyśli, że to właśnie chodzi o niego. Otóż szczecinianie nie lubią, gdy mówi się o nich, że mieszkają nad morzem. To prawda, mają do morza tak daleko, jak krakowiacy do Tatr. I oto pewien warszawiak prosi w hotelu w Szczecinie o pokój z widokiem na morze. "Niestety, tak wysoki nasz hotel nie jest", odpowiada uprzejmie recepcjonistka.

Zadanie (znów raczej dla uczniów). Jak wysoko trzeba się wzbić nad Szczecin, by zobaczyć morze? Możesz przyjąć, że odległość tego grodu od Bałtyku to 100 kilometrów. A Śnieżkę?

Wracamy do głównego zadania: jakiej wysokości wieża musi być ustawiona w najdalszym końcu Placuszka, by było ją widać ze środka? Nie mamy efektu zakrzywienia, a i dzięki rozsądnej polityce ekologicznej - o dbałości Placuszkan o swoją planetę było wyżej - powietrze jest bardzo przezroczyste. Pozostaje sprawa rozdzielczości wzroku, owej minuty kątowej. Ta jednostka odchodzi w zapomnienie. To jedna sześćdziesiąta stopnia. A zatem kąt BOA na rysunku 1 może mieć co najwyżej jedną sześćdziesiątą stopnia. Obejdziemy się bez trygonometrii. Dla tak małych kątów długość łuku jest prawie równa długości cięciwy, zatem kąt BOA to

kąta pełnego. Długość odcinka OA to

Okrąg o tym promieniu ma długość

Po podzieleniu przez 21600 otrzymujemy mniej więcej 0,6788. Jednostkami są megametry. Wieża ma mieć zatem wysokość około 6,8 kilometra. Niedługo takie będą i na Ziemi, w Dubaju. Ale Placuszkanie są zdolnymi inżynierami, a poza tym, no właśnie, przejdę do najbardziej interesującej części: wyliczenia grawitacji na Placuszku.

Należę do umiarkowanych zwolenników zdalnej nauki, przynajmniej jeśli chodzi o uczniów starszych klas i studentów. W szkole podstawowej, sorry, to jednak nie ma sensu. Ale wiem, że krytykować łatwo, zaś działać - trudniej. Nie mamy wyboru. Co to ma wspólnego z tematem artykułu?

Jak wiemy, prawa grawitacji odkrył Isaac Newton. Mało kto wie, że opracował je w domowym zaciszu, bo uniwersytet został zamknięty (w 1665 roku) z powodu zarazy. Używając współczesnej terminologii, po prostu pracował zdalnie. Chyba przez Internet, bo przecież Internet istniał zawsze. Podstawowym prawem grawitacji jest (a w każdym razie tak twierdzi Newton), że dwa ciała punktowe (to znaczy takie punkty matematyczne, obdarzone jednak masą) przyciągają się z siłą proporcjonalną do każdej z tych mas i odwrotnie proporcjonalną do kwadratu odległości między nimi. Współczynnik proporcjonalności G, nazywany jest stałą grawitacji:

Nature, and Nature’s Laws, lay hid in night.
God said, Let Newton be! and all was light.
Alexander Pope, 1688-1744

Przyrody wszelkie dzieło w pomroce leżało.
Bóg rzekł: "Niech będzie Newton" - i jasno się stało.
Przekład Julian Tuwim

Newton jest największym uczonym wszech czasów, ale
i najbardziej fortunnym, bo tylko jeden człowiek może
po raz pierwszy odkryć prawa Wszechświata.
Joseph Louis Lagrange, 1736-1813

2. Zenit, północ i wschód w stolicy Placuszka, punkcie centralnym O

Fizycy lubią tak zwaną zasadę antropiczną. Mówi ona mniej więcej tyle, że istnienie Wszechświata jest cudem, a raczej przypadkiem. Gdyby stałe fizyczne były choć trochę inne, nie tylko nie byłoby nas, ale w ogóle planet gwiazd ani piłki nożnej. Szczególnie w to ostatnie trudno uwierzyć. A mnie pasjonują badania stałej grawitacyjnej. Czy da się ją wyznaczyć zupełnie dokładnie? Oczywiście nie. To nie jest tak, jak z wykładnikiem 2 w mianowniku wzoru Newtona. Tam "musi być" dwa. Świat by się zawalił, gdyby było 2,0001.

Obliczmy, ile waży Placuszkanin, mieszkający w stolicy O - centralnym punkcie "wieczka".

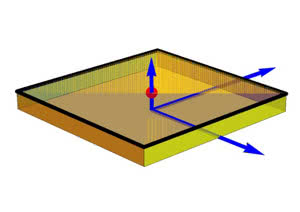
Placuszkanie żyją na wieczku (górnej podstawie) prostopadłościanu z rysunku 2. Obliczmy wektor siły, z jaką punkt O jest przyciągany przez całą planetkę. Oczywiście siła ciążenia działa "w dół", czyli prostopadle do płaszczyzny planetki, czyli w kierunku wektora "pionowego" - przeciwnego do strzałki "w górę" na rysunku 2. Co trzeba zrobić? Dla Czytelników znających analizę matematyczną sprawa jest oczywista: należy obliczyć taką całkę:

a całkujemy po x i y od -16,5 do 16,5, zaś po z od 0 do 0,01.

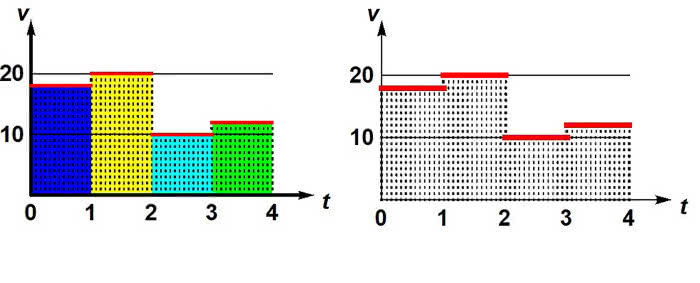
Postaram się wytłumaczyć i innym Czytelnikom, o co tu chodzi. Zacznę od omówienia samego słowa "całka". Staropolskie słowniki podają kilka znaczeń tego słowa, ale najważniejsze z nich to, hm, niewinna dziewczyna. W każdym (chyba) języku indoeuropejskim całka (teraz mówię o całce matematycznej) to integrał (z lokalnymi odmianami). Tylko po polsku jest inaczej. To zawdzięczamy Janowi (1756-1830) i Jędrzejowi (1768-1838) Śniadeckim, forsującym polską terminologię naukową (stąd i ostrosłup, graniastosłup, przyprostokątna i przeciwprostokątna). Zapamiętajmy: całkować = scalać. Poniższy przykład zatem każdy zrozumie. Wybrałem się w sobotę na wycieczkę rowerową. Jestem mocno starszym panem, jeżdżę powoli. Jaką drogę przebyłem, jeżeli przez pierwszą godzinę jechałem z prędkością 18 km/h, przez drugą 20 km/h, trzecią godzinę (powolutku, miłą, leśną drogą) 10 km/h, a czwartą - już zmęczony, do domu 12 km/h? To jasne: 18+20+10+12=60 km. Uff, to dla mnie dużo! Nie, to chyba nie byłem ja… Zobaczmy to na wykresie (3).

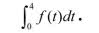3. Najkrótszy kurs rachunku całkowego: Prędkość rowerzysty, o którym pisałem, to funkcja (oznaczmy ją literką f) opisana czerwoną linią (składającą się z czterech części). Przebyta droga to suma pól prostokątów: 18+20+10+12. Na osiach jest czas w godzinach i prędkość w km/h, a zatem jednostki, jakie trzeba dopisać do wyniku, to kilometry. I tak po prostu obliczyliśmy całkę Obliczanie całek bywało i jest skomplikowane. Ale w XXI wieku wystarczy wziąć stosowny program komputerowy. Trzeba tylko rozumieć, jaką całkę mu napisać. Od tej pracy jeszcze nas nie uwolnił

Sądzę, że maturzyści zrozumieją, skąd się wzięła funkcja pod całką potrójną przy obliczaniu siły grawitacji na Placuszku. Jesteśmy w środku górnej podstawy Placuszka, w punkcie (0,0,0). Siła ciążenia działa prostopadle do dołu - przeciwnie do kierunku narysowanej tam strzałki. Weźmy pod uwagę punkt p=(x, y, z) w Placuszku ("w" – znaczy na powierzchni lub wewnątrz). Z punktem (0,0,0) łączy go wektor w = [x, y, z]. Ma on długość

a zatem

to składowa pionowa wektora o kierunku w i o jednostkowej długości. Kwadrat odległości punktu p od (0,0,0) to x² + y² + z². Siła, z jaką punkt ten oddziałuje na (0,0,0), jest proporcjonalna do

Musimy ją zrzutować na kierunek pionowy, stąd wyrażenie widoczne pod całką. Zdaję sobie sprawę, że może to zbyt enigmatyczne tłumaczenie. Można postąpić inaczej: podzielić Placuszek ma małe kawałeczki, dla każdego z nich wyliczyć siłę na jaką oddziałuje na (0,0,0) i wyniki dodać. Ale to jest bardziej skomplikowane.

No, dobrze. Wynikiem całkowania jest, z dobrym przybliżeniem, 0,62815. Matematyk jest zadowolony - dostał wynik liczbowy. Ale fizyk zapyta, co to znaczy? W jakich to jest jednostkach? W megametrach, w metrach to będzie 628150. Co pamiętamy ze szkolnej fizyki? Trzeba teraz tę liczbę pomnożyć przez stałą grawitacji i przez gęstość naszej planetki. A zatem mnożymy 628150 metrów przez 6,67384·10^-11(stałą grawitacji wyrażoną w jednostkach

Zacznijmy od jednostek: metry razy

metry na sekundę kwadrat. Czego są to jednostki, metr na kwadrat sekundy? Co nam to przypomina? Bingo! W takich jednostkach mierzy się przyspieszenie grawitacyjne (i każde inne przyspieszenie)! Jakie ono jest w punkcie O Placuszka? Bierzemy kalkulator: 625500·6,67·10^-11·240000=10,06 (w sensownym przybliżeniu). Och! Przyspieszenie ziemskie wynosi 9,81 m/s², a placuszkowate 10,06 m/s². Niewielka różnica. Ważylibyśmy tylko ciut więcej. Proszę jednak zwrócić uwagę, że gdyby gęstość planetki była porównywalna z gęstością Ziemi, to małe Placuszkanki ważyłyby około kilograma, a zapaśnicy sumo nawet trzy.

Ale literacko ciekawsze jest życie na planecie, którą nazwę (jako odkrywca) Kostką Szarego Mydła (w skrócie KSM). Wyobraźmy sobie planetę w kształcie regularnego sześcianu. Aby miała objętość i masę zbliżoną do ziemskiej, krawędź sześcianu powinna mieć 10270 km (czyli 10,27 megametra), a każdy uczeń powinien umieć to wyliczyć. Ale widać, że "chyba się zgadza": obwód Ziemi to 40 tysięcy kilometrów a Kostki Mydła trochę ponad 41000. Objętość sześcianu o krawędzi 10270 km to przecież 10270³=1,0832·10¹² kilometrów sześciennych (Ziemia ma też tyle, z dobrym przybliżeniem). Umiemy już obliczyć przyspieszenie mydlane (tzn. na powierzchni KSM). Nie napiszę już stosownej całki, podam tylko wynik: 26,67. Zatem przyspieszenie mydlane to 26,67∙10⁶∙6,67∙10^-11∙5,515=9,81 i wiemy, że to jest wartość przyspieszenia w metrach na sekundę do kwadratu. Tyle samo, co na Ziemi. Nic interesującego? Wprost przeciwnie. Co się dzieje na biegunie?

Rysunek. 4

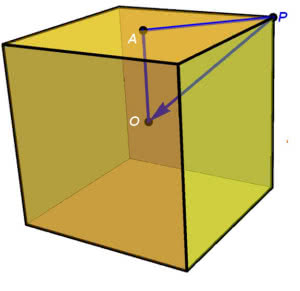
Ominę całkowanie; siła ciążenia "na biegunach" (czyli w narożnikach sześcianu) to 65% ciążenia w punkcie centralnym. Czy to się zgadza "ze zdrowym rozsądkiem"? Tak - wierzchołki są dalej od centrum. Ale bez obliczeń możemy odkryć zdumiewającą topografię okolic podbiegunowych. Zobaczmy. Pion to kierunek siły ciążenia. Działa ona do środka sześcianu. Spójrzmy na rysunek 4. Linia ukośna OP na tym rysunku to pion na biegunie planetki. A zatem w tamtych okolicach jest bardzo stromo. Jaki jest kąt nachylenia zbocza? Zaraz zobaczymy.

A zatem na KSM oczy mówią nam, że ziemia jest płaska, ale pozostałe zmysły się gubią: jesteśmy lżejsi o jedną trzecią, ale coraz ciężej iść, bo jest okropnie pod górę. Jednak nie ma to jak nasza stara Ziemia.

Tangens kąta AOP jest równy

To jest kąt prawie 55 stopni! Tak stromo jest na KSM w pobliżu bieguna. Jak wyobrazić sobie taką stromiznę? Posłużę się przykładem. Gdy stoimy nad Czarnym Stawem nad Morskim Okiem, to najwyższy wierzchołek Polski (Rysy) jest nad nami o mniej więcej 43 stopnie, a średnie nachylenie ścieżki (prowadzącej w dużej części zakosami) to tylko 20 stopni! Niewiele łagodniejsze jest przejście na drugą stronę przez "przełęcz" - środek krawędzi sześcianu. Tak kąt nachylenia ściany do pionu jest równy 45 stopni. Wątpliwe, czy istoty żyjące na różnych ścianach tej kostki spotkałyby się… przed wynalezieniem samolotu!

Osobną sprawą jest zmienność pór roku na Placuszku. Przy założeniu, że obraca się on wokół prostej prostopadłej do niego i nachylonej do ekliptyki tak jak ziemska oś obrotu - pory roku będą bardzo podobne jak u nas. To nie jest trudna matematyka - ale fantazja matematyczna też musi mieć swoje granice.

Wszystko to przerasta naszą wyobraźnię. Na Kostce Szarego Mydła oczy widzą płaszczyznę, nogi narastającą stromiznę - a całe ciało jakąś lekkość. Ale czy naprawdę to takie dziwne? Bo przecież mieszkańcy SKM nie mogą pojąć, że istnieją planety kuliste, na których ludzie po drugiej stronie chodzą do góry nogami. Oczy ludzi (tych na kulistej planecie) widzą płaszczyznę, a dalekie statki wynurzają się z morza najpierw masztami, dopiero potem całym pokładem.

A wszystko jest bardzo proste. Mieszkamy tu od zawsze. Przywykliśmy. Normalne jest to, do czego jesteśmy przyzwyczajeni. Nie zmieniajmy Ziemi, bo już nam daje sygnał, że przedobrzyliśmy!

Michał Szurek