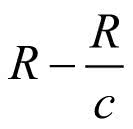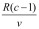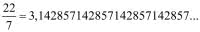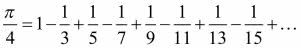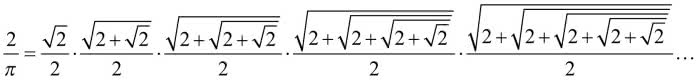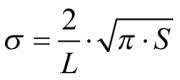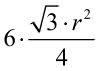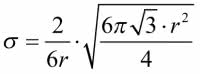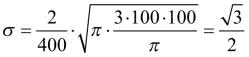Pi razy oko

Zwyczaj uhonorowania tej liczby, wyrażającej stosunek obwodu koła do jego średnicy i niekiedy nazywaną dlatego stałą Archimedesa (a w niemieckojęzycznym kręgu kulturowym także ludolfiną), pochodzi z USA (zobacz także: Uroki spirali Archimedesa). Czternasty marca to "po amerykańsku" 3.14, stąd ten pomysł. Polskim odpowiednikiem mógłby być 22 lipca, a to dlatego, że ułamek 22/7 dobrze przybliża π, co wiedział już… Archimedes. No, ale 14 marca przypada w lepszym czasie dla towarzyszących imprez.

Owo trzy i czternaście setnych to jedna z niewielu wiadomości matematycznych, które zostają nam ze szkoły na całe życie. Każdy wie, co to znaczy "pi razy oko". Tak bardzo przyjęło się to w języku, że nawet trudno wyrazić to inaczej, a równie zgrabnie. Gdy spytałem w warsztacie samochodowym, ile może kosztować naprawa, mechanik zastanowił się i orzekł: "pi razy oko osiemset złotych". Postanowiłem wykorzystać sytuację. "To znaczy w grubym przybliżeniu?". Mechanik chyba myślał, że nie dosłyszałem, bo powtórzył: "Nie wiem dokładnie ile, ale pi razy oko to będzie 800".

Kuć i orać w dzień zawzięcie.
Bo plonów niema bez trudu.
Złocisty szczęścia okręcie! Kołyszesz.
Kuć. My nie czekajmy cudu.
Robota - to potęga ludu.

O co tu chodzi? W pisowni sprzed drugiej wojny światowej "nie ma" pisało się łącznie i to zostawiłem. Nie mamy tu do czynienia z przesadnie górnolotną poezją, choć podoba mi się myśl, że "złocisty szczęścia okręt kołysze". Pytanie do uczniów: co znaczy ta myśl? Ale co innego jest wartością tego tekstu. Liczby liter w kolejnych słowach to cyfry rozwinięcia pi. Zobaczmy:

π ≈ 3,141592 653589 793238 462643 383279 502884 197169 399375 105820 974944 592307 816406 286208 998628 034825 342117 067982 148086 513282 306647 093844 609550 582231 725359 408128 481117 450284 102701 938521 105559 644622 948954 930381 96

W 1596 roku uczony holenderski pochodzenia niemieckiego Ludolph van Ceulen obliczył wartość liczby pi z dokładnością do 35 cyfr po przecinku. Potem wyryto te cyfry na jego grobie. Liczbie pi poświęciła wiersz i nasza noblistka, Wisława Szymborska. Szymborską fascynowała nieokresowość tej liczby oraz to, że z prawdopodobieństwem 1 każdy ciąg cyfr się tam pojawi, na przykład numer naszego telefonu. O ile pierwsza własność przysługuje każdej liczbie niewymiernej (co powinniśmy pamiętać ze szkoły), o tyle druga jest trudnym w dowodzie interesującym faktem matematycznym. Można znaleźć nawet aplikacje, oferujące: podaj mi swój numer telefonu, a powiem ci, gdzie jest on w liczbie pi.

Gdzie okrągłość, tam pi. Jeżeli mamy koliste jezioro, to droga piechotą dookoła jest 1,57 razy dłuższa niż wpław. Oczywiście nie znaczy to, że przepłyniemy półtora czy dwa razy wolniej, niż przejdziemy. Podzieliłem rekord świata w pływaniu na 100 metrów przez rekord świata w biegu na 100 metrów. Ciekawe, że dla mężczyzn i dla kobiet wynik jest prawie ten sam i wynosi 4,9. Pływamy 5 razy wolniej niż biegamy. Zupełnie inaczej jest z wiosłowaniem - ale oto interesujące zadanie. Ma dość długą fabułę.

Uciekając od goniącego go Złoczyńcy, przystojny i szlachetny Dobry wypłynął łódką na jezioro. Złoczyńca biega po brzegu i czeka, aż zmusi go do przybicia do brzegu. Biega oczywiście szybciej, niż Dobry wiosłuje, natomiast w biegu po płaskim Dobry jest szybszy. Jedyną więc szansą dla Złego jest dopadnięcie Dobrego przy brzegu - celny strzał z rewolweru nie wchodzi w grę, bo Dobry ma cenną informację, którą Zły chce posiąść.

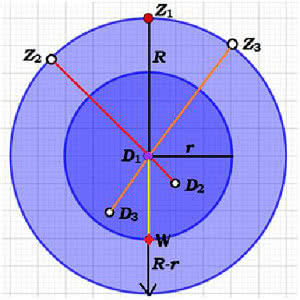
Dobry przyjmuje następującą strategię. Pływa po jeziorze, stopniowo przybliżając się do brzegu, ale pilnując, by zawsze być po przeciwnej stronie niż Zły, który biega chaotycznie to w lewo, to w prawo. Pokazuje to rysunek. Niech położeniem wyjściowym Złego będzie Z₁, a Dobrego - środek jeziora. Gdy Zły przejdzie do Z₁, Dobry podpłynie do D₁, gdy Zły będzie w Z₂, Dobry w D₂. Płynąć będzie zygzakiem, ale zachowując zasadę: jak najdalej od Z. Jednak w miarę oddalania się od środka jeziora, Dobry musi zataczać coraz większe kręgi i w pewnym momencie nie daje już rady zachować zasady "być po przeciwnej stronie Złego". Wtedy wiosłuje z całych sił do brzegu, licząc, że Zły nie zdąży obiec jeziora. Czy Dobremu się uda?

Odpowiedź zależy od tego, jak szybko potrafi wiosłować Dobry w stosunku do wartkości nóg Złego. Przyjmijmy, że Zły biega z prędkością v i że jest to c razy szybciej niż prędkość Dobrego na jeziorze. Największy okrąg, po którym Dobry może wiosłować, by utrzymać się w opozycji do Złego, ma zatem promień c razy mniejszy od promienia jeziora. Na rysunku mamy więc R = cr . W punkcie W nasz Dobry zaczyna już wiosłować do brzegu. Ma do przebycia 

 z prędkością

Zajmuje mu to  czasu.

Zły goni co sił w nogach naokoło. Ma do przebycia połowę obwodu, a więc πR , co zajmie mu sekund czy minut, w zależności od przyjętych jednostek. Jeżeli będzie to więcej niż 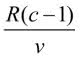 nastąpi happy end:

Dobry ucieknie. Proste rachunki pokazują, że musi być c<π+1. Jeżeli Zły biega szybciej niż 4,14 razy szybciej, niż wiosłuje Dobry, sprawa kończy się źle. I tu także interweniuje nasze pi.

Co okrągłe, to ładne. Spójrzmy na fotografię trzech ozdobnych talerzyków - mam je po Rodzicach. Jakie jest pole krzywoliniowego trójkąta między nimi? To proste zadanie; odpowiedź na tej samej fotografii. Nie dziwimy się, że we wzorze występuje ludolfina - bo przecież gdzie okrągłość, tam pi.

Użyłem prawdopodobnie nieznanego słowa: ludolfina. Tak nazywa się liczba pi w niemieckojęzycznym kręgu kulturowym, a to wszystko za sprawą Holendra (a właściwie Niemca mieszkającego w Holandii - w tych czasach narodowość nie była istotna), Ludolpha van Ceulena. W 1596 roku obliczył on 35 cyfr jej rozwinięcia na ułamek dziesiętny. Ten rekord przetrwał aż do 1853 roku, kiedy William Rutherford wyliczył 440 miejsc. Rekordzistą w ręcznych obliczeniach został (już chyba na zawsze) William Shanks, który po latach pracy opublikował (w 1873 roku) rozwinięcie do 702 cyfr. Dopiero w 1946 roku okazało się, że 180 końcowych cyfr jest błędnych - zostało jednak 527 poprawnych. Samo odkrycie błędu było interesujące. Już niedługo po opublikowaniu wyniku Shanksa podejrzewano, że "coś jest źle" - w rozwinięciu było podejrzanie mało siódemek. Nieudowodniona wciąż (grudzień 2020) hipoteza powiada bowiem, że wszystkie cyfry powinny występować z tą samą częstością. To skłoniło D.T. Fergusona do przejrzenia obliczeń Shanksa i znalezienia "uczniowskiego" błędu!

Potem pomagano już sobie kalkulatorami i komputerami. Obecnym (grudzień 2020) rekordzistą jest Timothy Mullican (50 bilionów cyfr po przecinku). Obliczenia zajęły… 303 dni. Pobawmy się: ile miejsca zajęłaby ta liczba, wydrukowana w standardowej książce. Do niedawna drukarska "strona" tekstu to było 1800 znaków (30 wierszy po 60). Zmniejszmy znaki i marginesy strony, upchnijmy 5000 znaków na stronie i drukujmy książki tysiącstronicowe. Zatem 50 bilionów znaków zajęłoby 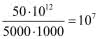 dziesięć milionów książek. Nieźle, prawda?

Nasuwa się pytanie, po co wszystko, jaki jest sens takich zmagań? Ujmując rzecz ze skrajnie ekonomicznego punktu widzenia: dlaczego podatnik ma płacić za takie "rozrywki" matematyków? Odpowiedź nie jest trudna. Po pierwsze, van Ceulen wynalazł do obliczeń sztabki rachunkowe, przydatne potem do obliczeń logarytmicznych. Gdyby mu powiedziano: proszę zbudować sztabki rachunkowe, odparłby: a po co? Podobnie nie przyniosło by też sukcesu polecenie: panie kolego Roentgen, proszę wynaleźć sposób prześwietlenia ciała ludzkiego. Jak wiemy, odkrycie to nie było całkiem przypadkowe, ale było jednak ubocznym efektem innego rodzaju badań.

Po drugie, przeczytajmy, co pisze Timothy Mullican. Oto reprodukcja początku jego pracy. Profesor Mullican zajmuje się cyberbezpieczeństwem, a liczby pi to takie drobne hobby, na którym po prostu testował swój nowy system cybersecurity.

A że w działalności inżynierskiej 3,14159 jest wystarczające z nawiązką, to inna sprawa. Zróbmy proste obliczenie. Jowisz jest odległy od Słońca o 4,774 Tm (terametr=1012 metrów). Do obliczenia długości obwodu takiego koła o takim promieniu z absurdalną przecież dokładnością 1 milimetra wystarczyłoby przyjąć π=3,1415926535897932.

Następna fotografia przedstawia ćwiartkę koła, ułożoną z klocków Lego. Zużyłem 1774 klocki i dało to pi równe w przybliżeniu 3,08. Nie najlepiej, ale czegoż się spodziewać? Koła nie da się ułożyć z kwadratów.

O właśnie. Swoją sławę liczba π zawdzięcza kwadraturze koła - problemowi matematycznemu, który czekał ponad 2000 lat na rozwiązanie - od czasów greckich. Czy da się za pomocą cyrkla i linijki skonstruować kwadrat o polu równym polu danego koła?

Określenie "kwadratura koła" też przeniknęło do języka potocznego jako symbol czegoś niemożliwego do wykonania. Ciśnie mi się pod klawisz pytanie, czy czymś takim są próby zasypania rowu wrogości, dzielącego obywateli naszego tak pięknego kraju? Ale już uciekam z tego tematu, bo pewnie czuję się tylko na gruncie matematyki.

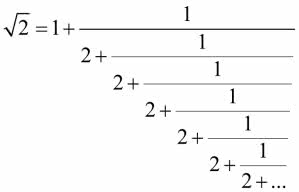
I znów to samo - rozstrzygnięcie problemu kwadratury koła nie pojawiło się w ten sposób, że autor rozwiązania, Charles Lindemann, w 1882 roku zawziął się i w końcu mu się udało. Do pewnego stopnia tak, ale był to wynik natarcia szerokim frontem. Matematycy nauczyli się, że liczby są różnych rodzajów. Nie tylko całkowite, wymierne (czyli ułamki) i niewymierne. Niewymierność bywa też lepsza i gorsza. Pamiętamy może ze szkoły, że liczbą niewymierną jest √2 - liczba wyrażająca stosunek długości przekątnej kwadratu do długości jego boku. Jak każda liczba niewymierna, ma ona rozwinięcie nieokresowe. Przypomnę, że rozwinięcie okresowe jest cechą liczb wymiernych, czyli ilorazów liczb całkowitych:

Ciąg cyfr 142857 powtarza się tutaj bez końca. Nie zdarzy się to dla √2 - między innymi na tym polega niewymierność. Ale można inaczej:

(ułamek ciągnie się w nieskończoność). Widzimy tu regularność, ale innego typu. Liczba pi nie ma nawet takiej regularności. Nie można jej otrzymać, rozwiązując równanie algebraiczne - to znaczy takie, w którym nie ma ani pierwiastkowania, ani logarytmowania, ani funkcji trygonometrycznych. Z tego już wynika, że jest niekonstruowalna - zakreślanie okręgów prowadzi bowiem do funkcji kwadratowych, a linii - prostych - do równań pierwszego stopnia.

Odszedłem może od głównego wątku. Dopiero rozwój całej matematyki spowodował, że możliwy był powrót do źródeł - do antycznej pięknej matematyki myślicieli, którzy stworzyli nam europejską kulturę myśli, tak kwestionowaną obecnie przez niektórych.

Z niezliczonej liczby wzorów przedstawiających wybrałem dwa. Pierwszy z nich wiążemy z nazwiskiem Gottfrieda Wilhelma Leibniza (1646-1716).

Ale znał go (wzór, nie Leibniza) średniowieczny uczony hinduski Madhava z Sangamagrammy (1350-1425). Przekaz informacji w owych czasach nie był rewelacyjny - łącza internetowe często się zawieszały, a do telefonów komórkowych nie było baterii (bo w ogóle nie wynaleziono jeszcze elektroniki!). Wzór jest ładny, ale bezużyteczny do obliczeń. Ze stu składników otrzymamy "ledwie" 3,15159.

Trochę lepszy jest wzór Viète’a (tego od równań kwadratowych), a jego formuła daje się łatwo zaprogramować, bo kolejny składnik w iloczynie jest pierwiastkiem z poprzedniego, powiększonego o dwa.

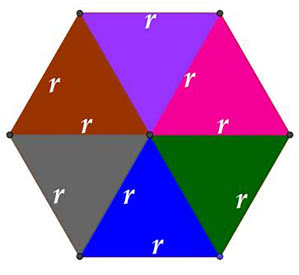
Wiemy, że koło jest okrągłe. Można powiedzieć, że jest okrągłe na 100 procent. Matematyk zapyta: a czy może coś być okrągłe nie na sto procent? Pozornie to oksymoron, czyli zwrot zawierający ukrytą sprzeczność, tak jak na przykład gorący lód. Ale spróbujmy wymierzyć, jak bardzo okrągłe mogą być figury. Okazuje się, że dobrą miarę daje taki oto wzór, w którym S jest polem, a L obwodem figury. Sprawdźmy, że koło jest naprawdę okrągłe, że sigma jest 1. Pole koła to πr² , obwód 2πr . Wstawiamy… i widzimy, że się zgadza. A jak okrągły jest kwadrat? Obliczenia równie proste, nawet nie będę ich przytaczał. Weźmy sześciokąt foremny, wpisany w okrąg o promieniu r. Obwód to oczywiście 6 r.

Pole

A sześciokąt foremny? Jego obwód to 6r, pole to

Mamy zatem

czyli mniej więcej 0,952. Sześciokąt jest "okrągły" na ponad 95%.

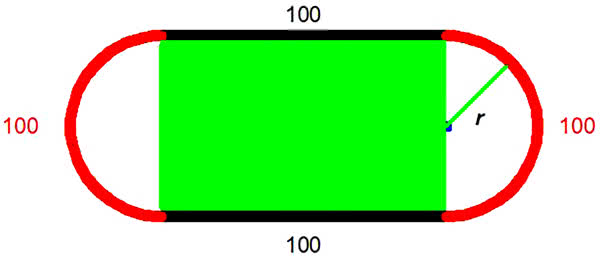
Ciekawy wynik daje obliczenie okrągłości stadionu sportowego. Według przepisów IAAF, proste i łuki mają mieć po sto metrów, choć dopuszczalne są odchylenia. Pamiętam, że stadion Bislet w Oslo był wąski i długi. Piszę "był", bo nawet biegałem na nim (amatorsko!), ale ponad 40 lat temu. Zobaczmy:

Jeżeli łuk o promieniu r ma 100 metrów, to promień tego łuku ma  metrów. Pole trawnika jest równe 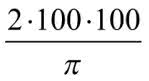 metrów kwadratowych, a pole poza nim (tam, gdzie są skocznie)  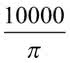co daje łącznie  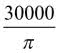metrów kwadratowych. Podstawmy to do wzoru:

Czy więc okrągłość stadionu sportowego ma coś wspólnego z trójkątem równobocznym? Bo przecież wysokość trójkąta równobocznego jest właśnie tyle razy dłuższa od boku. To jednak przypadkowa zbieżność liczb, ale ładna. Mnie się podoba. A Czytelnikom?

Cóż, co okrągłe, to ładne - chociaż niektórzy mogą zaprotestować, bo wirus, który tak się nam wszystkim daje we znaki, jest okrąglutki. Przynajmniej tak go malują.

Michał Szurek