Zgaduj, zgadula, w której ręce złota kula

Potem nawet studenci geografii nie wiedzą, co to jest długość geograficzna (autentyk, zdarzyło mi się – miałem wykład na stosownym wydziale uniwersytetu). Spotkanie było nadzwyczaj udane, brawa dla dyrekcji i trzech nauczycielek, które to wszystko organizowały. Nauczanie to nie tylko przekazywanie wiedzy w 45-minutowych porcjach od 8 rano do drugiej czy trzeciej po południu. No, a obecnie, w zdalnym nauczaniu, i tak wszystko jest inaczej. Coraz częściej nauczyciele dyskutują, jak zmienić tradycyjny system klasowo-lekcyjny na… no właśnie, na co? Pamiętajmy, że eksperymentujemy na "żywym organizmie"- na dzieciach. Gdzie jest ta złota kula, zawierająca mądrości życiowe?
Opiniuję wnioski uczniów o stypendium Krajowego Funduszu na Rzecz Dzieci, przeznaczone dla dzieci wybitnie zdolnych. Było tam zawsze dość dużo zgłoszeń z Leszna. W tym roku też były, ale co drugie dziecko (gimnazjalista) pisało: "odkąd moja nauczycielka, pani I. wyjechała, straciłem zainteresowanie matematyką". Pojawiło się natomiast dużo zgłoszeń z mało reprezentowanego dotąd Lublina. Zagadka dla Czytelników: do jakiego miasta przeniosła się z Leszna się pani I.? Do Lublina? Tak, ale jak na wpadliście, Czytelnicy?
Powierzchnia kuli to sfera (z łacińskiego sphera 'kula, niebo'). Ten matematyczny termin wszedł do języka potocznego: mówimy o sferach wpływów wielkich mocarstw, sferze czyichś zainteresowań i sferach towarzyskich. "Och, ona nie jest z naszej sfery" mówiła hrabina o tej ślicznej wiejskiej dziewczynie, w której zakochał się panicz. I wszyscy wyobrażali sobie wtedy społeczeństwo jako koncentrycznie ułożone powłoki, nieprzenikające się wzajemnie: na jednej my, w najlepszym oczywiście towarzystwie, na innej ta biedna dziewczyna i nawet geometria powiada "Kopciuszku: zostań tam, gdzie jesteś!".
W ogóle nietrudno ulec fascynacji kształtem sferycznym. Wystarczy pogodnej nocy znaleźć się pod gołym niebem, z dala od miast, a najlepiej na wysokiej górze i to zimą. Spójrzmy do góry: czyż nie widzimy wyraźnie sfery niebieskiej? Na niej przyczepione są dalekie gwiazdy, na ich tle po bliższych sferach poruszają się błądzące ciała niebieskie: planety. Ptolemeusz uczył, że Ziemia jest środkiem Wszechświata i otoczona jest dziewięcioma koncentrycznie położonymi kryształowymi sferami.
Na siedmiu pierwszych z nich jest siedem znanych planet : Diana (=Księżyc), Merkury, Wenus, Apollo (= Słońce), Mars, Jowisz i Saturn. Ósma sfera zawierała gwiazdy stałe. Dziewiąta była jak pokrętło do regulowania chodu zegara: po niej poruszał się punkt równonocy wiosennej. W Średniowieczu dodano do tego systemu dziesiątą sferę: Primum mobile , jakby sprężynę, poruszającą wszystko siłę sprawczą, twardą powłokę oddzielającą świat od nicości. Pitagorejczycy wierzyli w harmonię sfer – że planety poruszające się po swoich sferach wydają nadzwyczaj przyjemne dźwięki. Świat jest przecież liczbą i muzyką.
W konkursie matematycznym dla uczniów, który zorganizowaliśmy na wspomnianej zielonej szkole, rywalizowały zaciekle dwie drużyny. Cóż, jedna wygrała (33:31), druga przegrała. Jak to w sporcie.
Algorytm podziału startujących na dwie drużyny jest tak ciekawy matematycznie, że omówię go dokładnie. Problemem jest tu oczywiście równomierna kwalifikacja mocniejszych i słabszych do zespołów. Ale co to jest równomierny? Pozornie najlepszy jest wybór losowy: każdy zawodnik wyciąga z pudełka karteczkę z napisem 1 lub 2 i idzie do odpowiedniej drużyny. Ale… przy rzucie monetą 10 razy tylko w 25 procentach przypadków wynik jest 5:5, to jest pięć orłów i pięć reszek. Widzimy zatem, że z prawdopodobieństwem 75 procent drużyny będą nierówne.
Jest jawnie niesprawiedliwy sposób, w którym dwaj wyznaczeni wcześniej kapitanowie wybierają członków swoich zespołów po kolei: raz ty, a raz ja. Pierwszy kapitan ma zawsze przewagę, może wybrać najlepszego z pozostałych. Podobnie jest w piłce nożnej przy rzutach karnych, które mają wyłonić zwycięzcę meczu pucharowego. Jedna z drużyn zawsze strzela pierwsza. Lepiej sobie poradzono w tenisie, gdzie zawodnik serwujący jest zawsze w lepszej sytuacji. W rozgrywce tiebreakowej po pierwszym serwisie zawodnika A, drugi serwuje dwa razy, potem dwa razy A i następnie po dwa serwisy na przemian B, A, … aż do przewagi dwóch punktów wygranych.
Taki sposób też nie bardzo nadaje się do wyboru dwóch zespołów uczniowskich. Sposób, który opiszę, stworzyli matematycy według pomysłu wziętego z tak zwanego algorytmu Steinhausa. Jest powszechnie stosowany w meczach matematycznych np. na zawodach przygotowawczych przed Olimpiadą. Ciekawe, że bardzo podobny system stosowaliśmy na moim podwórku, gdy chcieliśmy "pograć w nogę" na pustym wtedy placu za domem. Chłopców było dużo (pochodzę z pierwszej fali powojennego wyżu demograficznego).
Algorytm jest taki. Moneta rozstrzyga, który z kapitanów (A czy B) wybiera pierwszy. Niech będzie nim A. Wskazuje on gracza, a teraz (uwaga!) kapitan B decyduje, czy gracz ten pójdzie do pierwszej, czy drugiej drużyny. I tak dalej na przemian. Jeden wskazuje gracza, drugi przydziela. Drugi wskazuje, pierwszy przydziela.
Zwróćmy uwagę na trudności psychologiczne. Jeśli kapitan A wskaże najlepszego, to B natychmiast zaliczy go do swojej drużyny. Jeżeli wskaże najsłabszego, to B powie: "bardzo dobrze, weź go sobie" … ale po chwili role się odwrócą. Jak zatem grać?
Pomaga tu pewna socjotechnika i psychologia społeczna. Szczególnie, gdy w wybór zaangażowana jest młodzież, liczą się bardzo sympatie i antypatie a nie tylko też bliżej nieokreślony "poziom". Konkretnie, po wskazaniu któregoś z zawodników przez kapitana A, kapitan B ocenia, czy wskazany kolega (wskazana koleżanka) jest subiektywnie w górnej, czy dolnej połówce uczestników. Czy ja go/ją chcę, czy niech idzie do A? Mam wybór. Jeśli widzę wskazanego uczestnika w górnej połówce, biorę go do siebie, a jeśli w dolnej, zostawiam. Rolę się zmieniają, teraz B wskazuje, zaś A kwalifikuje. Postępuje tak samo. Jeżeli ocenia wskazanego dobrze, bierze go do siebie, jeśli źle – zostawia. W ten sposób każdy z kapitanów za każdym razem bierze lepszego (lub co najmniej równego!). Każdy uważa, że zrobił lepszy wybór, że jego drużyna jest lepsza. Matematyka potrafi dogodzić ludziom nawet w tak delikatnych sprawach.
A oto pytania, z jakimi zmagali się uczestnicy konkursu na mojej zielonej szkole. Jak zobaczymy, niektóre pytania są niematematyczne, podchwytliwe i zabawne.
- Co to jest loksodroma?
- Masz 20 kulek. Jak wysoki jest czworościan, który można z nich ułożyć? Ile potrzeba kulek na czworościan złożony z 10 warstw?
- Wyszedłem z namiotu. Poszedłem kilometr na zachód, potem kilometr na północ i potem kilometr na południe. W ten sposób znalazłem się przy swoim namiocie. Siedział przed nim niedźwiedź. Jakiego był on koloru?
- Ile kul o średnicy 1 zmieści się w kuli o średnicy 2?
- Uporządkuj od najmniejszej do największej piłki używane w następujących sportach: tenis ziemny, tenis stołowy, piłka nożna, siatkówka, koszykówka, piłka wodna.
- Jaka piłka nie jest ani kulista ani owalna (jak w rugby czy futbolu amerykańskim)?
- Podaj przysłowia i powiedzenia związane z kulą.
- Wymyśl dowcip zaczynający się "Przychodzi kula do lekarza."
- W sześcian o krawędzi 1 metr wpisano kulę. Czy w narożniku zmieści się jeszcze kulka o promieniu 20 cm?
- Czy sześcian o krawędzi 1 cala zmieści się w kuli o promieniu 1 centymetra?
- Jak wiadomo, dawniej kule armatnie były rzeczywiście kuliste. Dziś nie są. Co zadecydowało o zmianie kształtu pocisków?
- Objętość kuli wynosi p2 centymetrów sześciennych. Oblicz jej pole powierzchni.
- Czy okrąg o promieniu

może leżeć na kuli o promieniu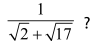
- W pojemniku B jest 100 kul białych, w pojemniku C jest 100 kul czarnych. Wybieramy losowo 10 kul z pojemnika B i wrzucamy je do C. Ze 110 kul, które są teraz w C, wybieramy losowo 10 i wrzucamy je do B. Czy teraz jest więcej kul czarnych w B czy białych w C?
- Jaką figurą może być cień kuli?
- Który równoleżnik na Ziemi ma długość połowy równika?
- Planetka T pokryta jest równomiernie trawą. W pewnym punkcie planetki uwiązana jest koza. Jaka powinna być długość łańcucha, żeby w zasięgu kozy była dokładnie połowa trawy na planetce?
- W poemacie Pan Tadeusz Stolnik został zastrzelony. Do kogo należał karabin, z którego pochodziła kula?
- Ile wyrazów czteroliterowych (sensownych lub nie) można utworzyć przez przestawianie liter w wyrazie KULA?
- Czy istnieje kula styczna do wszystkich krawędzi sześcianu? Jeśli tak, to oblicz jej promień. Jeśli nie - to uzasadnij.
Komentarze. Zachęcam do dowiedzenia się (od czego Internet?), co to jest loksodroma.
Zadanie 2 jest całkiem trudne. Z dwudziestu jednakowych kul można ułożyć czworościan 10+6+3+1 (dziesięć kul na spodzie, potem sześć, trzy i jedna). Taka bryła ma cztery warstwy, ale jest niższa niż czterokrotna średnica każdej kuli - kulki wchodzą bowiem w zagłębienia niższego piętra.
Omówię to zadanie, choć … nie rozwiążę. Zostawię to chętnemu Czytelnikowi. Mam na myśli między innymi mojego przyjaciela, Kazimierza ze Szczecina. Kaziu – na pewno spodoba Ci się. Zadanie przecież kojarzy nam się miło ze szkołą. Taki stosik widzimy na fotografii. Pomarańcze te były bardzo dobre … Każda przekupka wie, że najlepiej ustawić jabłka, pomarańcze, cytryny i inne twarde owoce właśnie tak (pomidory mogłyby się zgnieść). Otóż dopiero pod koniec zeszłego wieku rozwiązano zadanie, które postawił w 1610 roku Johannes Kepler, a mianowicie jak wykazać matematycznie, że to rzeczywiście najlepszy sposób. Mówiąc bardziej precyzyjnie, jednakowe kule zajmują najmniej miejsca w przestrzeni, gdy są ustawione właśnie tak. Jest to nieco mniej niż 75 procent. Jest fascynującym zagadnieniem matematycznym, jak to jest w przestrzeniach o większym wymiarze, ale to znów temat na inny artykuł.
Szkołą do której chodziłem, hm, dość dawno, jeszcze była jedenastoletnia. W przedostatniej, dziesiątej klasie, przez cały rok była w zasadzie geometria i trygonometria. Pamiętam zbiór zadań Henryka Paśniewskiego - czegóż tam nie było? Czworościany, graniastosłupy, i ostrosłupy przekrajane na wszelkie możliwe sposoby. A właśnie, było mało zadań o kuli. Bo to trudne, nawet narysować ją niełatwo.
Od tego czasu trygonometria w szkole została bardzo okrojona, zdegenerowana. Jak każdy starszy człowiek, mam tendencję do wspominek, że wszystko "wtedy" było lepsze. To oczywiście nieprawda. Nie wszystko. Trygonometria nie jest już tak bardzo potrzebna w codziennej pracy inżyniera i geodety. Przestały być potrzebne drewniane wieże triangulacyjne, stawiane na wierzchołkach gór. Jedna z największych stała na Lubaniu nad Krościenkiem. Miała nawet góralską nazwę "patryja". No, dobrze, wystarczy tych dygresji. Spójrzmy na rysunek. Wyznaczamy najpierw długość odcinka s . Kąt a ma przecież 60 stopni. Mając AC, wyznaczymy BC , a następnie wysokość BH. Ale jest to wysokość ściany bocznej naszej piramidki z pomarańczy. Wysokość piramidki otrzymamy stąd mnożąc BH przez sinus kąta nachylenia ściany do podstawy, który … też trzeba wyliczyć, ale to łatwe i standardowe.
Czy mogę powiedzieć, ze "zadanie rozwiązane". Kojarzy mi się to niestety z coraz bardziej powszechnym nauczanie zdalnym. Siedzę przed ekranem i "gadam do obrazu", a studenci – bo tych nauczam - mają pracować według moich instrukcji. Zresztą sam się przecież tak nauczyłem Microsoft Teams, Inspery i innych gadżetów do prowadzenia takich zajęć. Instruktor siedział u siebie, ja u siebie, każdy popijał własną kawę, on "gadał do obrazu", a ja starałem się naśladować.
→ W szkole, w której uczę, już wiadomo, że nawet gdy "wróci normalność", wykłady będą się odbywać właśnie tak. Taka forma ma wiele zalet. To temat na inny artykuł. Pozwala nawet lepiej nauczyć się tym, którzy … chcą się nauczyć.
→ Niestety, takich nie jest tak dużo, jak się nam, nauczycielom, wydaje. Spóźniłem się z dostarczeniem tego artykułu do Redakcji, ale jeśli do Państwo czytają, to znaczy, że skończyło się dobrze. Mianowicie zdenerwowałem się zachowaniem studentów pierwszego roku, którym zostawiłem za dużo swobody na egzaminie. Wyciągnę wnioski i wrócą metody "policyjne". A mój nastrój spowodował, że zamiast kończyć tekst, poszedłem na długi spacer po zaśnieżonych polach pod Warszawą. Był mróz, zmarzłem…
→ Wróćmy do konkursu o kuli. Na pytanie 6 można było odpowiedzieć "piłka do metalu", albo "zgnieciona piłeczka pingpongowa". Za najlepszy dowcip (zadanie 8) uznaliśmy taki, gdzie kula skarży się lekarzowi "nie wiem, co mi jest, ale jestem cała skołowana." Dobry był też taki, w którym kula narzeka na bóle promieniste i że ją łupie w średnicy. Przysłowie związane z kulą (zadanie 7 ) jest w tytule artykułu, wiemy też, czym jest kula u nogi (to Ziemia, prawda?). Zadanie o kolorze niedźwiedzia ma długą brodę (oczywiście niedźwiedź był biały, bo taka marszruta może się zdarzyć tylko w okolicach podbiegunowych).
Kule armatnie (zadanie 11) nie są już kuliste, bo umiemy robić nagwintowane lufy, co nadaje pociskowi ruch obrotowy.
Ciekawe okazało się pytanie 13. Dawałem je potem nawet studentom. Próbowali brnąć w niezbyt zresztą sensowne obliczenia, przerażał ich ten pierwiastek z 17. Tymczasem zadanie jest banalnie proste. Kula o podanym promieniu jest malutka, a okrąg duży. Nie zmieści się. W pytaniu 18 właściwa odpowiedź była: do Moskala, któremu Jacek Soplica wyrwał karabin. Uczniowie odpowiedzieli błędnie: do Jacka.
Do kuli jeszcze wrócę, bo mnie bardzo pociąga. A dowodem jest poniższa "oda do kulistości".
Kulo! Bryło ty moja! Duża-ś czy malutka,
Taka sama okrągła jesteś dokolutka.
Wyśpiewać chcę dzisiaj całą twą urodę.
Mogę i równaniami. Lecz napiszę odę!
Ile cię trzeba cenić, ten tylko się dowie,
Kto cię widział. Lecz piękność twoją w całej ozdobie
Doceni, kto na zielonej szkole był w Sławkowie!
Twe piękno się od środka do brzegu rozciąga!
Twa geometria wszystkich jednako pociąga.
Ja od dziecka małego, już od przedszkolaka,
Chciałem zawsze zrozumieć, czemu jesteś taka.
Jakże ojcowskie słowa boleśnie te brzmiały:
"Dowiesz się, gdy dorośniesz. Dziś jesteś za mały!",
Kiedym jako pacholę i niewinne dziecię
Zgłębić twe tajemnicze pragnął cztery trzecie,
A jaka głęboka tkwiła w sercu zadra,
Gdym pożądał twe tajne cztery pi er kwadrat.
Jam strawił ulotnej niemało młodości,
Całkując w myśli twoje główne okrągłości,
A gdy się twarz młodzieńczym pokryła zarostem,
Ujrzałem taki trójkąt, co trzy kąty proste
Posiada. I zaraz mogłem rozgłosić, jak śliczna
Geometria na powierzchni jest twa eliptyczna.
A jak na młodzieńczą wpłynęło oskomę,
Gdyś pokazała mi wreszcie swoją loksodromę,
Co się każdego równo ima południka,
Pod tym samym tnąc kątem… A z tego wynika,
Że do nieskończoności długość krzywej rośnie,
I że oba bieguny oplata miłośnie.
Później, zapatrzony w twój tensor Riemanna
Obliczałem ja pola obszarów do rana
I na twojej powierzchni wdzięcznie zwanej sferą,
Krzywizny główne nigdy nie wyszły mi zero.
Tak mi pozostań wierna, stała, jednorodna,
Z każdej strony ta sama, miła i pogodna.
Miej ty zawsze same kołowe przekroje!
Zatęskni jeszcze do ciebie nieraz serce moje.
Niech teraz młodzi ludzie, nie znając siwizny,
Badają twe nieznane Gaussowi krzywizny.
Michał Szurek








