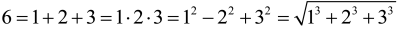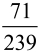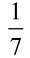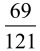Szósty miesiąc roku

Zatem z okazji czerwca opowiem o liczbie sześć. W mądrości ludowej jest ona dość duża: gdzie kucharek sześć, tam nie ma co jeść. Ale Adam Mickiewicz w "Reducie Ordona" wspomniał, że "sześć tylko miała harmat". Jan Brzechwa w zgrabnej rymowance wypomniał szóstce, że była oszustką i zrobiło się z tego ćwiczenie z ortografii: szóstka, ale oszustka.

Ale dojdę w tej opowieści do matematyki z bardzo wysokiej półki. Tę liczbę lubiliśmy od zawsze. W czasach starożytnych symbolizowała równowagę, stabilność i harmonię. Spójrzmy na fotografię 1, czyż nie wygląda to ładnie i harmonijnie? Szkoda tylko, że brak dwóch ogonków przy pomidorach nieco zakłóca symetrię.

Fotografia 1.

Sześć jest liczbą doskonałą. Tak nazywamy (od Starożytności) liczby, równe sumie swoich dzielników. Następną taką liczbą jest 28. W swoim znanym traktacie „O państwie Bożym przeciw poganom” święty Augustyn (jeden z ojców Kościoła, żył w latach 354-430) pisze:

To ze względu na doskonałość liczby sześć całość stworzenia dokonała została, jak opowiada Pismo Święte, przez sześciokrotne powtórzenie tego samego dnia, czyli w przeciągu sześciu dni. Wszak liczba ta jest pierwszą liczbą, która stanowi sumę swoich części, to jest sumę szóstej części, trzeciej części i połowy, czyli sumą jedynki, dwójki i trójki, które po dodaniu tworzą właśnie sześć.

Oto cztery początkowe liczby doskonałe:

6=1+2+3

28=1+2+4+7+14

496=1+2+4+8+16+31+62+124+248

8128=1+2+4+8+16+32+64+127+254+ 508+1016+2032+4064

Niezbyt trudno jest wykazać, że parzyste liczby doskonałe są postaci 2ⁿ(2ⁿ⁺¹-1), przy czym 2ⁿ⁺¹-1 musi być liczbą pierwszą (takie liczby pierwsze nazywają się liczbami Mersenne’a), w powyższych przykładach mamy n=1, 2, 4, 6. Nie wiadomo, czy istnieje nieparzysta liczba doskonała. Próby jej znalezienia się nie powiodły i wykazano, że jeżeli istnieje, to musi być... bardzo duża. Ale dowodu ogólnego nie ma. To bardzo trudne zadanie, a od pięćdziesięciu lat patrzymy z szacunkiem na zadania o wielkich liczbach. Potrzebne są wszędzie tam, gdzie chcemy mieć porządny szyfr, niemożliwy do złamania, przynajmniej teoretycznie. Podobno komputery kwantowe dadzą sobie radę z każdym szyfrem i wtedy wrócimy do wypróbowanej metody chowania wszystkiego w solidnej szafie.

Rysunek 2.

W prawie wszystkich kulturach przyjęto nosić pierścionek na serdecznym palcu i nawet to może mieć związek z doskonałością liczby 6. Otóż w starożytnym Egipcie wyobrażeniem liczby 6 była ręka z zagiętym tym właśnie palcem, a ponieważ szóstka jest doskonała, ten palec był najbardziej honorowy. Można wierzyć w to wytłumaczenie, można nie wierzyć, tak jak w całą pozostałą symbolikę liczb.

Nazwa ulubionej przez wielu z nas czynności: sjesta, pochodzi od nazwy godziny szóstej. W średniowieczu była to szósta godzina od wschodu słońca, czas na... sjestę.

Inne ciekawostki o liczbie 6:

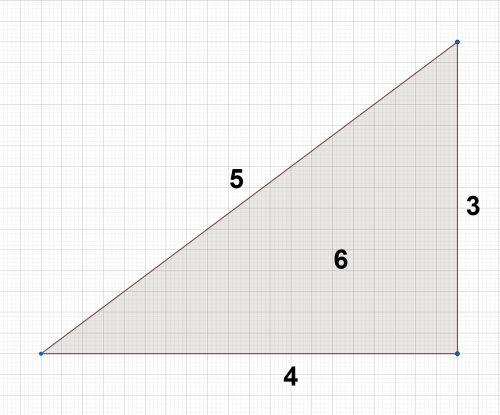
Trójkąt prostokątny o bokach długości 3, 4, 5 nazywany jest trójkątem pitagorejskim. Gdy na sznurku zrobimy węzły w odległościach 3, 4, 5, możemy dokładnie wyznaczyć w terenie kąt prosty. Pole takiego trójkąta jest równe 6.

I jeszcze jedna nieco kuriozalna, ale warta uwagi własność szóstki. Napiszmy trzy kolejne liczby, ale takie, by największa była podzielna przez 3. Niech dla przykładu będą to 2020, 2021 i 2022. Dodajmy je. To łatwe działanie; można w pamięci: wynikiem jest 6063. Dodajmy cyfry otrzymanej liczby: 6+0+6+3=15 i potem znów dodajmy cyfry, aż dojdziemy do liczby jednocyfrowej. W naszym przykładzie 1+5=6. Okazuje się, że zawsze tak będzie (o ile największa z wybranych liczb będzie podzielna przez 3). Sprawdźmy na innych liczbach, nawet tak olbrzymich, jak 9751287239, 9751287240, 9751287241. Sprawdźmy, że ostatnia dzieli się przez 3. To znaczy: kto nie wierzy, niech sprawdzi. Pytanie do młodych uczniów: czy pamiętasz cechę podzielności przez 3?

Dodajemy. Z pewnym zażenowaniem przyznaję, że posłużyłem się komputerem. Mój ojciec (matura: 1926) dodałby je, zanimbym zdążył wpisać do komputera - to znaczy do stosownego programu obliczeniowego. Ja wziąłem modny ostatnio program Wolfram Alpha:

38997512872696+38997512872697+38997512872698
↳ = 116992538618091

Tak czy owak, mam sumę. Dodaję cyfry:

1+1+6+9+9+2+5+3+8+6+1+8+0+9+1=69,

6+9=15, 1+5=6.

Własność ta, choć drobna i niepozorna, jest interesująca z dwóch powodów. Pierwszy z nich to, że została odkryta dość dawno, a mianowicie przez syryjskiego filozofa Jamblicha, żyjącego w latach 250-336. Był on jednym z ostatnich filozofów starożytności - zaliczamy go do neoplatoników - próbujących pogodzić odchodzącą już filozofię Sokratesa, Arystotelesa i Platona z nowymi realiami, ze zwyciężającym chrześcijaństwem. Po drugie, że nawiązuje do wielu zagadnień z naszego już dwudziestego pierwszego wieku. Komputery bowiem lubią takie zagadnienia: zrób coś, powtórz wiele razy - co otrzymasz na końcu? A może końca nie będzie? Na zajęciach w pewnej szkole informatyki dałem to studentom: napisz działający możliwie szybko program, który będzie obliczał, za którym razem otrzymam ową szóstkę, gdy wystartuję z danej liczby N. Nie było to trudne, choć stopień trudności zależał od biegłości studenta w programowaniu. Ale temu miało służyć ćwiczenie. Sam dla siebie sprawdziłem, jak będzie dla liczby 666!+1, 666!+2, 666!+3. Każda z nich ma po 1594 cyfry. Już za pierwszym razem otrzymałem sumę cyfr 6351, wobec tego potem idzie 6+3+5+1=15 i 1+5=6. Zgadza się.

Pięćdziesiąt, sześćdziesiąt lat temu matematyka przeżyła wielki boom. Po prostu odkryto jej nowe zastosowania i gwałtownie wzrosła liczba studentów (na Uniwersytecie Warszawskim w ciągu kilku lat trzykrotnie, ja byłem na początku fali), a potem absolwentów kierunków matematycznych, a ten nadmiar spowodował również szybkie poszerzanie się obszarów, do których matematyka się wtrąca. Jednym z nich jest… układanie klocków.

Gra w domino jest już mało popularna, ale może wszyscy wiedzą, że klocki domina to prostokąty złożone z dwóch kwadracików. A gdyby wziąć trzy? A cztery? A pięć? Mamy wobec tego tromino, tetramino, pentomino, heksamino i tak dalej. Przedrostki tetra-, pento-, heksa- są greckie. Departament Stanu USA mieści się w pięciokątnym Pentagonie, a widoczna czasami na parkingach trylinka daje wzór heksagonalny. Jeśli nie wiesz, co to jest "trylinka", to zajrzyj, gdzie trzeba. Za mojego dzieciństwa wiele ulic tak właśnie brukowano…

Sama zabawa nie jest nowa, już w starożytności znano wszystkie kostki pentomina. Spróbujesz sam narysować albo ułożyć z klocków?

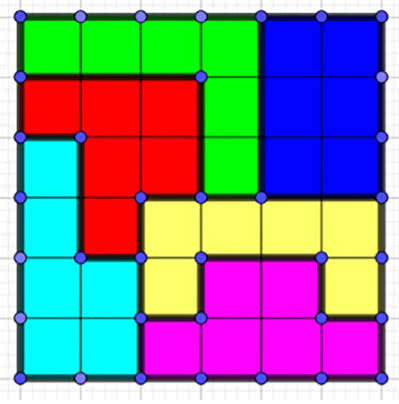
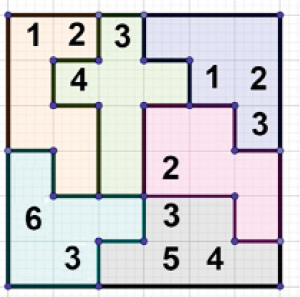
Pójdźmy krok dalej, przyjrzyjmy się kostkom heksamina, złożonych z sześciu kwadracików. Ile jest takich kostek? Aż 35. Nie będę rysował wszystkich. Proszę jednak spojrzeć na rysunek 3. Mamy tam sześć różnych "heksaminów", złożonych w kwadrat. Stwórz inne podobne układanki, czyli sześć różnych klocków "sześciokwadracikowych" wypełniających kwadrat. Ile ich możesz narysować? Nie wiem. Chyba nikt nie wie. Na pewno bardzo dużo.

Rysunek 3.

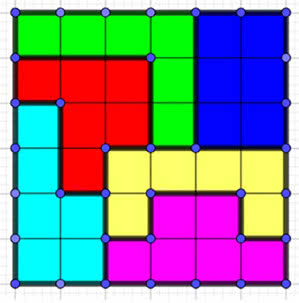
Od kilkunastu lat modna jest gra sudoku. Nawet w swojej podstawowej wersji jest ciekawa dla matematyka, o czym pisałem kilka miesięcy temu, a zapewne wrócę niebawem. Gra polega na wypełnieniu kwadratu liczbami 1, 2, 3, 4, … w pewien sposób, obwarowany ścisłymi regułami (matematyk nazwałby je "aksjomatami"). Na pewno wiecie Państwo, o co chodzi. Ale zachowajmy się jak matematycy, którzy poszukują wciąż możliwych uogólnień. Taka twórczość matematyczna jest w najwyższej cenie, za to dostaje się nagrody i awanse. Nie licząc jednak na wielkie zaszczyty, stwórzmy własne sudoku. Wpisz do diagramów z rysunków 4 i 5 liczby od 1 do 6 tak, by nie powtarzały się one ani w rzędach poziomych, ani pionowych, ani w sześciu zaznaczonych "heksaminach". W pierwszym diagramie mamy kwadrat podzielony na sześć takich samych części. Na rysunku 5 wszystkie są różne. Rozwiązanie… gdzieś w numerze. A "prawdziwe" zadanie polega na ułożeniu interesującego, ale i trudnego sudoku "heksaminowego". Reguły są takie: podział kwadratu ma być ciekawy z plastycznego punktu widzenia, ma być możliwie mało podanych liczb, ale rozwiązanie musi być tylko jedno. Może zacznij od diagramu z rysunku 6. Ornament nie jest może zbyt ciekawy, ale dobry na początek.

Rysunek 4.

Rysunek 5.

Rysunek 6.

Spójrzmy inaczej na kostki układanki. Zacznijmy od najprostszego, sześć kwadracików jeden za drugim (rysunek 7). Możemy tam zobaczyć po prostu siatkę z drucików. A gdy druciki, to coś może po nich biec. Może to być schemat połączeń kolejowych, wyciągów narciarskich albo sieć komputerowa. Biegną po niej megabajty informacji. Jaka jest przepustowość takiej sieci? O ważności tego zagadnienia nie trzeba nikogo długo przekonywać.

Rysunek 7.

Rysunek 8.

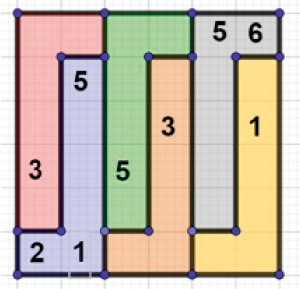
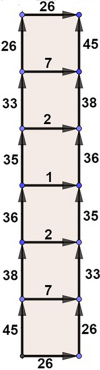
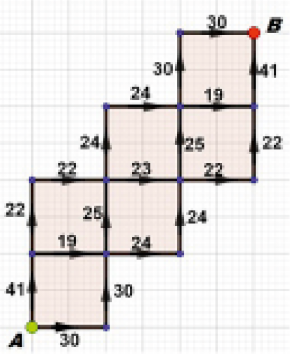
Konkretnie. Chcemy przesłać pewną liczbę, powiedzmy megabajtów, z A do B. Każdy odcinek ma przepustowość 1 MB, to znaczy, że w jednostce czasu (np. milisekunda) możemy nim przesłać 1 MB. Ile czasu zajmie przesłanie informacji określonego rozmiaru? Podobno przy przesyłaniu głosu np. Skype'em dzieli się nasz głos na składowe, które muszą spotkać się jednocześnie u odbiorcy. Piszę "podobno", bo nie znam się na tym, a tylko przeczytałem, zresztą w poważnym źródle. Odpowiedź jest dość nieoczekiwana. Aby wszystkie składowe spotkały się w punkcie końcowym, muszę podzielić dane wyjściowe w proporcji 45:26. Biegną one wtedy tak, jak pokazuje rysunek 8. Można zobaczyć, że suma liczb po dowolnej drodze z A do B jest zawsze taka sama: 26+26+33+35+36+38+45=239. W takim czasie odbiorca B dostanie wysłanych 45+26=71 jednostek informacji. Przepustowość sieci wynosi zatem

czyli około 0,3. Gdyby A i B były połączone jednym tylko przewodem długości 7, przepustowość byłaby równa

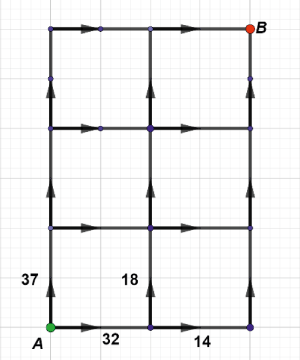
czyli około dwóch razy mniejsza. Nic dziwnego - wykorzystujemy zręcznie liczne obejścia. Co to znaczy "zręcznie"? To tak, jak każe matematyka! Skąd jednak wziąłem te liczby, 45 i 26? Och, po prostu napisałem laplasjan widocznego grafu, wyliczyłem jego macierz pseudoodwrotną i skorzystałem z odpowiedniego algorytmu. Tak, wiem, że tylko drobnej części Czytelników coś to powie. To pokazuje, że posługujemy się matematyką z wysokiej półki. Powiem jednak, że w każdym oddzielnym przypadku możemy to zrobić nie tyle prościej, co nie wchodząc na ową "wysoką półkę". Wystarczy ułożyć kilka równań i niech nasz elektronowy przyjaciel je rozwiąże. Na rysunku 10 masz zadanie: oblicz przepustowość widocznej tam sieci.

Rysunek 9.

Rysunek 10.

Wskazówka: dane wejściowe trzeba podzielić w stosunku 37:32, a w węźle po prawej stronie punktu A w stosunku 18:14. Jaka wyszła odpowiedź? Może

czyli około 0,570? Bardzo dobrze. Czy dziwi Cię, że przepustowość takiej sieci jest większa niż dwóch poprzednich? Sądzę, że zgadłbyś to od razu. Sieć z rysunku 10 jest bardziej zwarta.

Matematycy dwudziestego wieku byli dumni z tego, że badają nieskończoność i skomplikowane abstrakcyjne przestrzenie. Jeden z najbardziej znanych polskich matematyków wyraził się, że problemy dotyczącego zbiorów skończonych nie są prawdziwymi zadaniami matematycznymi - wystarczy przecież sprawdzić wszystkie możliwości. Ale to tylko mocno teoretyczne podejście. Coraz bardziej matematyka skręca właśnie w stronę badań struktury sieci, kryształów, ornamentów, analizy możliwości i wyboru optymalnej drogi. Problemy mało abstrakcyjne - przeciwnie, bardzo konkretne. Nie znaczy to, że rozwiązania są łatwe. Często wymagają zastosowania bardzo zaawansowanych metod. Ale dotyczy to przecież całej cywilizacji ludzkiej: jak bardzo skomplikowane są proste, codzienne urządzenia - choćby i ta "maszyna do pisania", za pomocą której wystukuję artykuł. Gdy zaczynałem swoją współpracę z "Młodym Technikiem" w 1976 roku, mogłem nawet przynieść tekst napisany ręcznie, długopisem na papierze. To sa uż ne vrati…

Na zakończenie zauważę, że przecież liczba sześć kojarzy się od razu z sześcianem. O tej prostej i miłej bryle pomówimy innym razem, może w sierpniu, a więc w szczycie wakacyjnym. Temat relaksowy, ale co ma wspólnego sierpień z sześcianem? Jak to co? Liczbę osiem. Przecież tyle wierzchołków ma sześcian. Fotografia 11 pokazuje "sześcienne sudoku" - na każdej ścianie mamy dziewięć różnych liczb od 1 do 9. Nie byłbym sobą, gdybym nie zadał Ci, młody Czytelniku (oczywiście niekoniecznie młody w sensie Peselu, ale młody duchem!), zadania: jakie liczby są na trzech niewidocznych ściankach?

Fotografia 11.

Czy wiesz, że pewien mój student nie wiedział, ile ścian ma sześcian? Dobrze jednak o nim (studencie, nie sześcianie) świadczy to, że gdy dowiedział się i zrozumiał, dlaczego ja się niepedagogicznie śmieję - długo się śmiał sam z siebie.

Michał Szurek