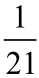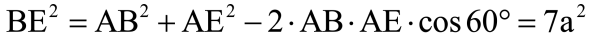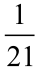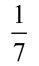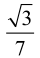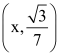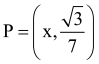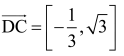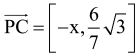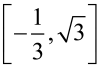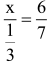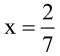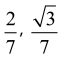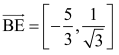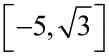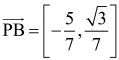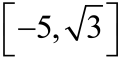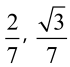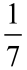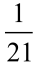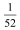Matura 2021 i jedna dwudziesta pierwsza (2)

Oj, do prima aprilis jeszcze daleko. Uciekam do zagadnień, w których czuję się swobodnie, czyli do matematyki.
W tym roku wiosna była chłodna, ale dzięki deszczom bardzo piękna. Wróciliśmy do półtorawiekowej tradycji: kwitnące kasztany = matura. Ze wzruszeniem zobaczyłem zadanie maturalne w starym, dobrym stylu. Brzmiało mniej więcej tak.
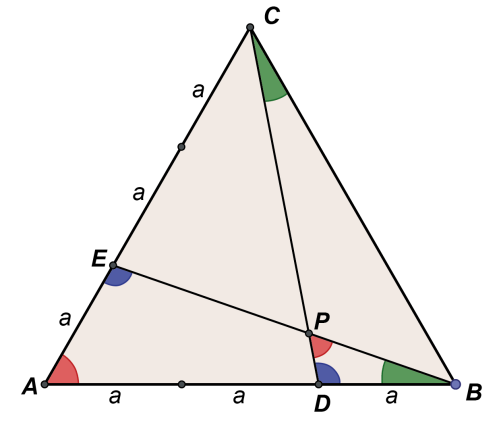
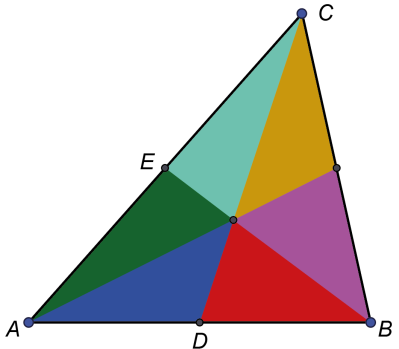
Na bokach AB i AC trójkąta równobocznego odcięto odcinki AE i BP w jednej trzeciej długości tych boków. Wykaż, że pole trójkąta DPB
to pola całego trójkąta ABC.
Oto rozwiązanie (szkolne, typowe, bez fajerwerków) (1). Trójkąty BCD i ABE są oczywiście "takie same" (poprawnie: przystające albo izometryczne). Można użyć odpowiednich reguł przystawania, ale najprościej zauważyć, że powstają one w analogiczny sposób: tu i tam odcinamy tę samą część boku dużego trójkąta. Skoro tak, to prosta obserwacja kątów pokazuje, że trójkąt BPD ma takie same kąty, jak ABE. Takie trójkąty nazywają się podobnymi. Pamiętamy, że pola figur podobnych mają się do siebie tak, jak kwadraty długości odpowiednich boków. Muszę tu zrobić dygresję. Uczyłem kiedyś matematyki studentów geografii. Prawie zawsze kładłem ich na takim oto pytaniu. Weźmy mapę Polski w skali 1 do miliona. To arkusz mniej więcej metr na metr; trochę mniejszy. Polska ma ponad 30 milionów obywateli, a zatem na tej mapie powinno się zmieścić 30 ludzi. Gdzie sens, gdzie logika?
No tak, bywałem często złośliwy i groziłem studentom, że zadzwonię do szkoły, w której się uczyli i powiem, jak ich nauczono... Ale wracajmy do naszego zadania Matura ’21.
Uczymy jeszcze szczątków trygonometrii - kiedyś tak potrzebnej w miernictwie. Abiturienci powinni znać twierdzenie cosinusów. Nie będę tego twierdzenia przypominał, od razu zastosuję do trójkąta ABE. Za jednostkę długości a przyjmę jedną trzecią boku trójkąta ABC. Wtedy uniknę rachunków na ułamkach. Spójrzmy znów na rysunek 1.
Jak się rzekło, pola figur podobnych mają się do siebie tak, jak kwadraty długości odpowiadających rozmiarów liniowych (dla wielokątów: boków, dla kół: promieni albo średnic). Widzimy, że pole trójkąta, o który nam chodzi, jest siedem razy mniejsze od pola ABE, a pole ABE jest trzy razy mniejsze od pola ABC (bo AE jest jedną trzecią AC). Biorę kalkulator i już po minucie (no, może dwóch) mam wynik: trzy razy siedem to przecież dwadzieścia jeden, oczko, hurra. Mogę dalej rozwiązywać maturę…
Co to jest tak zwane "dobre zadanie"? To tak, jak dobry temat muzyczny: powinno łatwo wpadać w ucho, mieć prostą konstrukcję, nieskomplikowaną fabułę, dostarczać skojarzeń, dawać możliwości transkrypcji, przeróbek, uogólnień, podpowiadać możliwości dalszego rozwijania tematu i jak w muzyce - dawać się interesująco rozwiązać. Użyłem tu terminu rozwiązanie właśnie w sensie muzycznym. Rozwiązanie akordu polega na przejściu z dysonansu na konsonans. Akord buduje pewne napięcie, rozwiązanie rozładowuje. Słyszymy dokładnie to, co chcielibyśmy usłyszeć i co nam podpowiada intuicja… i wychowanie, osłuchanie, obycie z muzyką. Czyż nie jest i tak w matematyce? Zadanie buduje napięcie, rozwiązanie rozładowuje.
Wprawny nauczyciel pomyśli tak: w tym rozwiązaniu twierdzenie cosinusów jest trochę na siłę - użyte jeden raz i do kąta 60°. To musi się dać zrobić prościej…
Zapach kwitnących kasztanów skojarzył mi się z podobnym zadaniem, które rozwiązywałem kiedyś. Kiedyś, dawno temu. Też w maju.
Zadanie… i rozwiązanie (2). Trójkąt ABC jest prostokątny i równoramienny, punkt D jest w jednej trzeciej CB, odcinek BP jest prostopadły do AD. Wyznacz kąt (tzn. jego miarę) CPD.
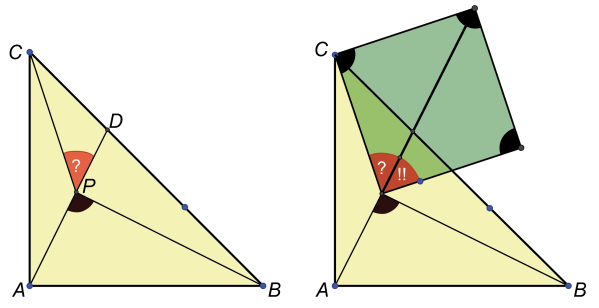
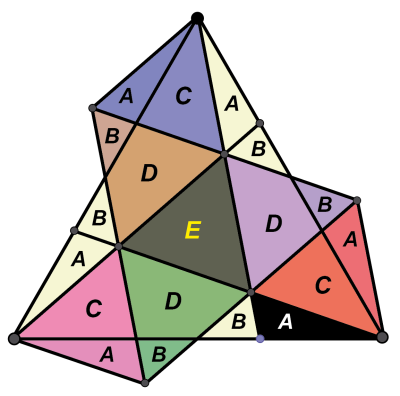
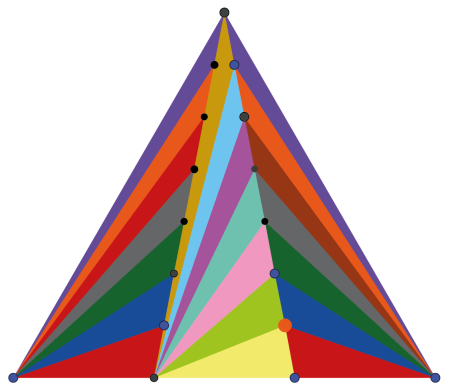
"Zadanie maturalne musi się dać tak samo rozwiązać" - pomyślałem. Na maturze nie zdążyłbym, ale w ciszy domowego ogródka narysowałem rysunek (3), który pokazuje, dobitnie i kolorowo, że widoczny tam duży trójkąt równoboczny ma pole równe siedmiokrotności tego małego, szarego, widocznego wewnątrz. Ponieważ zaś pole trójkąta, o który chodzi w zadaniu, jest tercją (to znaczy jedną trzecią) małego trójkąta równobocznego E (widać to najlepiej na trójkącie niebieskim u góry), zatem pole A to jedna dwudziesta pierwsza dużego.
Coraz bardziej wciągałem się w zadanie. Mamy XXI wiek, programy obliczeniowe uwalniają nas od rachunków. Nie tylko uwalniają - one lubią rachować, obliczać, kalkulować. No to dlaczego nie zrobić im przyjemności?
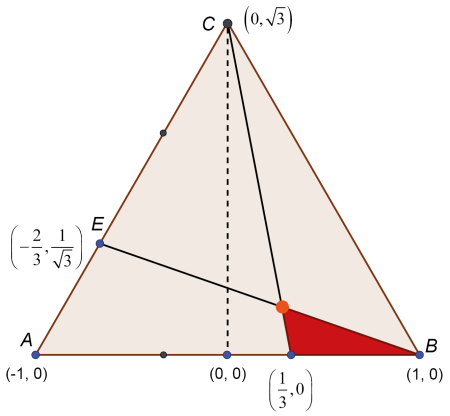
Wprowadziłem układ współrzędnych, jak na rysunku (4). Współrzędne punktów D, E wyznaczyłem natychmiast (punkty te są w jednej trzeciej AB, AC). Teraz zacząłem myśleć. Jeszcze ludzie są lepsi niż komputery. Hm, ponieważ DB to jedna trzecia podstawy, więc jedyną szansą, żeby DPB miało
pola ABC jest, by wysokość trójkąta IB była
wysokości całego trójkąta ABC. Czyli współrzędną y punktu P musi być
Musi i już. Bez tego ani rusz. To się nazywa myślenie heurystyczne. A więc, punkt przecięcia prostych BE i CD "musi" mieć drugą współrzędną . Mogę wyznaczyć równania tych prostych i wyjdzie. Ale to nieestetyczne i więcej rachunków. Nie chce mi się wyznaczać równań tych prostych, zresztą nie pamiętam stosownych wzorów! Mówię poważnie - nie pamiętam szkolnych wzorów na równanie prostej. Mnie w szkole nikt tego jeszcze nie uczył, a na studiach poznałem prostsze i łatwiejsze do zapamiętania. Odwrócę zatem kota ogonem.
Znajdę na prostej CD punkt
i zobaczę, czy należy on do prostej BD. Szukam. Niech
Jeszcze nie wiem, czy to ten sam punkt, co na rysunku. Właśnie o to biega! Wyznaczam. Wektor
wektor
Jeżeli P leży na prostej BD, to wektory te są proporcjonalne. No to dla jakiego x ten wektor jest równoległy (= proporcjonalny) do
? Zobaczmy:
skąd (jeśli umiemy rachować na ułamkach, a wielu maturzystów potrafi!)
Sprawdzamy teraz, czy punkt P o współrzędnych
leży na prostej BE. Wyznaczam wektor
Jest on równoległy (proporcjonalny) do
Teraz ten drugi,
i też jest (kochamy go za to) równoległy do
Wykazaliśmy wobec tego, że wyrachowany punkt P, to znaczy punkt P o współrzędnych
, wyleguje się na obu prostych, czyli jest tym, co i na rysunku. A zatem wysokość trójkąta BPB z rysunku to istotnie
wysokości całego trójkąta. I cóż nam więcej trzeba? Zadanie rozwiązane. A może to uda się wyrysować?
Oczywiście. Podzielmy trójkąt na 21 mniejszych (21=oczko, zawsze to miło!).
Wycinanka łowicka (5) jako rozwiązanie zadania maturalnego… z matematyki.
Od czasu do czasu przyznaję się, że "zamordowałem geometrię". Na własny użytek napisałem program (a raczej zestaw prostych komend), który realizuje cztery podstawowe konstrukcje geometryczne: prowadzenie prostej przez dwa punkty, wyznaczanie punktów wspólnych dwóch prostych, prostej i okręgu i dwóch okręgów. Potrafię w ten sposób "rozwiązać" bardzo wiele zadań, nawet z poziomu olimpiady matematycznej. Na szczęście nie wszystkie (najgorzej jest z dwusiecznymi). Zadanie, o którym dziś tyle piszę, należy do najłatwiejszych. Rozwiązanie zmieściłoby się w SMS-ie. Ale wiem, że tak nie można by nauczać.
Od dwóch lat jednak nauczam studentów moich studentów (informatyki) zupełnie inaczej niż… przez całe moje życie zawodowe. Mam z nimi zajęcia z algebry i podstaw matematyki. Uczę ich po pierwsze posługiwania się programami obliczeniowymi (w tym oni błyskawicznie okazują się lepsi ode mnie), po drugie - i tu zachowuję nad nimi przewagę - rozumienia tego, co mówi do nich komputer. Czy aby na pewno o to ci chodziło w obliczeniach? A jeśli tak, to jak zinterpretujesz wynik? Obliczenie nie jest końcem, ale początkiem! A jak wykorzystasz otrzymany wynik?
No, właśnie, pisałem o zaletach "dobrego zadania" - to takie, które prowokuje do myślenia. Jedną myśl jest oczywista. Zamieńmy trójkąt równoboczny ABC na prostokątny równoramienny. "Zrobi się", zadanie jest o podobnym stopniu trudności, a wynik… och! Weź, Czytelniku, papier kratkowany, linijkę i narysuj starannie taki trójkąt, jaki ja narysowałem… szczerze mówiąc za pomocą Geogebry. Czy widzisz, że pole czerwonego trójkącika jest równe
trójkąta prostokątnego (6)? Policz kratki! Wysokość czerwonego jest jedną siódmą wysokości całego. Tak jak poprzednio! Czy to jest dowód matematyczny? Niestety, nie, ale gdybym sprawdzał Twoją maturę, dałbym Ci dodatkowe punkty za pomysłowość.
Weźmy inny trójkąt (7). Do licha, znów jedna dwudziesta pierwsza! Oj, to może zawsze będzie "oczko". Jak myślisz, Czytelniku?
Każdy matematyk zastanowi się od razu: a gdyby dzielić boki AB i AC nie na trzy, a na cztery części… A potem na pięć, sześć, …, ogólnie na n części. Chwila. Zacznijmy od n=2. To zadanie dla uczniów szkół podstawowych. Jak i poprzednio, dobry rysunek pomaga jak… tyczka w skoku.
Punkt I to punkt sprawiedliwości (8) - środek ciężkości trójkąta ABC. Gdy w domach A, B i C mieszka po tyle samo ludzi, sklep powinien być w punkcie P.
Matematyk nie spocznie, zanim nie rozwiąże przypadku ogólnego (9): dzielimy jeden i drugi bok na n-części. Nie jest to trudne zadanie. Pole małego trójkąta jest n(n2-n+1) razy mniejsze od dużego. Daje to ciąg:
6, 21, 52, 105, 186, 301, 456, 657, 910, 1221, 1596, 2041, 2562, 3165, …
w którym na miejscach 3, 37, 53, 103, 137, 153, 203, 237, 253, 303, 337, 353, … i tak dalej. Ale "jak dalej" - to już należy do matematyki z wysokiej półki (10).
Za miesiąc - znów o tym samym zadaniu i o liczbie 21. Ale za dwa miesiące - już o czym innym.
Michał Szurek