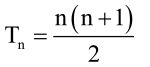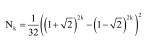Klocki, monety, kasztany i Encyklopedia Ciągów Liczbowych

Uczniowie zdziwili się od razu pierwszym zadaniem. Oto ono:

Zadanie 1. Narysuj 1+2+3+4+5. Ułóż z klocków.

Po chwili konsternacji (jak można narysować dodawanie? A czy może chodzi o narysowanie liczby 15?) i w jednej i w drugiej grupie uczniów odważny uczeń podszedł do tablicy (ciekawe, że przyszło im to samo do głowy!)
"No, tak, dobrze", powiedziałem, "ale może ładniej, z kółeczkami ?". Domyślili się, o co mi chodzi. Powstały dwa rysunki. "O świetnie", ale ułóżmy to z monet. Szybko powstały dwie układanki,

1. Jeden dodać dwa, dodać trzy, dodać cztery, dodać pięć

A ja pokazałem trzecią - z piłeczek pingpongowych, ułożonych na tle książki Hugona Steinhausa "Kalejdoskop matematyczny" i czworościanów ułożonych z pałeczek i kuleczek magnetycznych.

"No, a teraz ułóżmy to jeszcze raz z klocków, ale tak, żeby zrozumieć ogólny wzór na sumę kolejnych liczb: 1+2+3+… +n. Wyjaśniłem, że matematyka jest tam, gdzie odkrywamy ogólną prawidłowość, wzór, formułę. Jednostkowe łamigłówki są oczywiście ciekawe i mogą być bardzo trudne - ale właśnie tym różnią się od matematyki, że nie odkrywają ogólnych zależności.

2. Piętnaście groszy ułożone w trójkąt równoboczny i trójkąt prostokątny

3. Piętnaście piłeczek sklejonych w trójkąt równoboczny. Ile sklejeń musiałem wykonać?

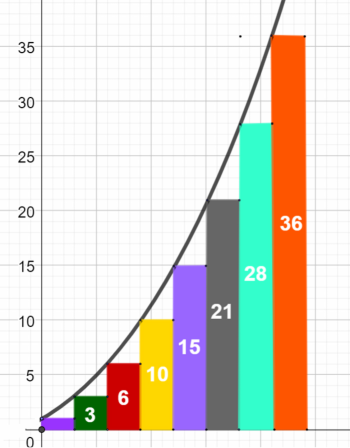
Możemy się domyślić z rysunku, że liczby takie jak sumy 1+2, 1+2+3, 1+2+3+4, a ogólnie 1+2+3+ …+ n nazywamy liczbami trójkątnymi. Napiszę trzydzieści początkowych liczb trójkątnych. Jak można się domyślać, obliczył mi to komputer. No, nie sam, tylko stosowny program, który ja (człowiek!) uruchomiłem.

Zobaczmy to na wykresie.

4. Wysokości słupków odpowiadają kolejnym liczbom trójkątnym 1, 3, 6, 10, 15, 21, 28, 36. Wysokości te zwiększają się kolejno o 2, 3, 4, 5, 6, 7 i 8. Wierzchołki prostokątów leżą na paraboli

Do wyprowadzenia ogólnego wzoru na liczby trójkątne już należało uczniów podprowadzić, by odkryli coś samodzielnie, ale w końcu ułożyliśmy taki kwadrat (rys. 5). Trzeba się w niego wpatrzeć, żeby zrozumieć, o co chodzi. No, to wpatrujmy się. Jest to kwadrat 6 na 6, ale ogólnie widzimy n na n. Ale niech będzie nie n na n, tylko (n+1) na (n+1). To przecież wszystko jedno, a potem końcowy wzór będzie prostszy. Na przekątnej, tej z północnego zachodu na południowy wschód (często mówię na nią: od Szczecina do Przemyśla!) są monety ułożone orłami do góry. Jest ich sześć - zgodziliśmy się, że to jest dla nas n+1 .

5. Trzydzieści sześć groszy ułożone w kwadrat

Nad i pod przekątną złożoną z orłów mamy dwie piramidki jak z rysunku 2, czyli dwa razy po 1+2+3+4+5, a ogólnie 1+2+3+…+n. A więc 2·(1+2+3+…+n)+(n+1)=(n+1)².
Sumę kolejnych liczb nazwaliśmy liczbą trójkątną,
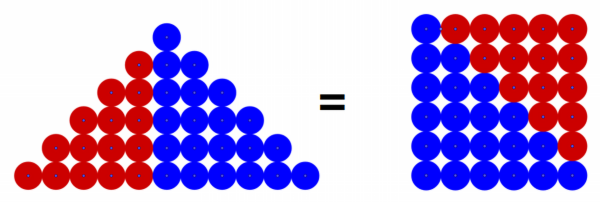
Tn. Mamy więc 2·Tn+(n+1)=(n+1)².
Nietrudno stąd wyprowadzić końcowy wzór na liczby trójkątne:

Wzór prosty, ale ciekawy. Dałem następne zadanie.

Zadanie 2. Narysuj 1+3+5+7. Oblicz 1+3+5+7+9+11+13+15+17+19+21+23+25+27+29+31. Zapisz wzorem. Oblicz.

Tu poszło gorzej. Najpierw obliczaliśmy
1=1, 1+3= 4, 1+3+5=9, 1+3+5+7=16,
1+3+5+7+9=25, 1+3+5+7=9+11= 36,
ale uczniom ciąg 1, 4, 9, 16, 25, 36, … z niczym się nie kojarzył. Nawet mnie to zdziwiło, ale gdy im powiedziałem, co to za ciąg, to z kolei oni zdziwili się, że tego nie dostrzegli …, przecież to kolejne kwadraty:
12, 22, 32, 42, 52, 62, …

Ale jak to zobaczyć na monetach, albo klockach? Można na kilka sposobów. Na przykład tak:

6. Trzydzieści sześć jako liczba trójkątna i jako liczba kwadratowa

Spójrzmy na rys. 6. Po lewej stronie mamy (w poziomych rzędach) kolejne liczby nieparzyste: 1, 3, 5, 7, 7, 9, 11. Układamy kółka w kwadrat i widzimy, że suma jest równa 36. Suma kolejnych liczb nieparzystych jest kwadratem pewnej liczby. Pewną sztuką jest zgadnąć, jakiej. Oto i stosowny wzór:

1+3+5+…+(2n-1)=n².

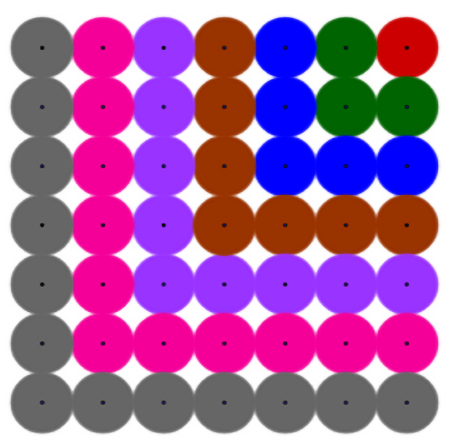
I jeszcze ułóżmy inaczej sumę kolejnych liczb nieparzystych (rys. 7). Kółka tego samego koloru wypełniają "korytarzyk" w kształcie litery L (poza pojedynczym kółkiem w prawym górnym narożniku). Ile jest kółek poszczególnych kolorów? Liczby od góry: 1, 3, 5, 7, 9, 11, 13 a łącznie wypełniają kwadrat 7 na 7. Wszystko się zgadza. Suma liczb nieparzystych 1+3+5+7+9+11+13 to 7².

7. Suma kolejnych liczb nieparzystych

Ponieważ, jak wspomniałem, pora roku była kasztanowa, więc uczniowie chętnie stworzyli układankę jak na rys. 8. Trzydzieści sześć kasztanów można ułożyć w kwadrat albo w  trójkąt równoboczny.

8. Kasztany jako pomoc w nauce arytmetyki

8. Kasztany jako pomoc w nauce arytmetyki

A czy są inne liczby trójkątno-kwadratowe, większe od 36? Są. Jest ich nieskończenie wiele, ale najmniejsza po 36 to dopiero
1225=352=1+2+3+…+49,
a potem idą
41616, 1413721, 48024900, 1631432881, 55420693056, 1882672131025, 63955431761796, 2172602007770041, 73804512832419600, 2507180834294496361, 85170343853180456676, 2893284510173841030625, …

Sam zdziwiłem się (wiele lat temu), gdy dowiedziałem się o istnieniu OEIS, The On-line Encyclopedia of Integer Sequences. Są w niej najrozmaitsze ciągi liczbowe, które są interesujące z matematycznego punktu widzenia. Liczby trójkątne mają kod A000217 (można powiedzieć, że to ich PESEL), a liczby trójkątno-kwadratowe kod A001110. Można się z tej encyklopedii dowiedzieć, jak wiele interesujących własności one mają i że nawet w XXI wieku ich własności nie są do końca odkryte. Ale już w 1778 roku Leonhard Euler odkrył ogólny wzór na ten liczby. Oznaczane są one symbolem Nk , a zatem N1=1, N2=36, N3=1225. Wzór ten wygląda dość zawile:

Jeden z uczniów zadał kłopotliwe pytanie: czy to wszystko ma jakieś zastosowanie, czy to tylko tak sobie? Pytanie stawiane często matematykom. Co komu ze znajomości własności ciągów liczbowych? Można to pytanie postawić w jednym rzędzie z innymi: po co nam wiadomości o dawno wymarłych gadach, o budowie dalekich słońc, o Marsie sprzed miliona lat i Ziemi za milion lat, z czego zasłynął król Rurytanii Burburyk Pierwszy, co chciał powiedzieć Adam Mickiewicz przez swoje 44, dlaczego gramy Chopina (gdy to piszę, kończy się XVIII Konkurs Chopinowski) tak dalej i tak dalej. Jaki sens ma piłka nożna i zjeżdżanie na sankach po specjalnie spreparowanym lodowym torze?

9. Tytuł pracy Chena i Pana

No cóż, to wszystko jest dla matematyków po prostu interesujące, jak dla fanów muzyki kolejne wykonania klasycznych utworów, wciąż pięknych - to kolejna aluzja do Fryderyka Chopina. Ale matematyka jest w lepszej sytuacji. Chociaż nie wszystkie odkrycia matematyczne znajdują zastosowanie, to "jakoś tak jest", że bardzo wiele z tych odkryć biorą fizycy, inżynierowie, ekonomiści, informatycy, a nawet językoznawcy i literaturoznawcy. Trudno tylko powiedzieć, co i kiedy zostanie wykorzystane.

10. Alwyn Horadan (1923-2016) Źródło: https://binged.it/31EGOl6

Wielkie odkrycia biorą się niekiedy z przypadku. Jednym z przykładów jest odkrycie promieniotwórczości. Gdyby Roentgen nawet dostał "grant" na znalezienie metody prześwietlania ciała ludzkiego, pewnie by nic nie odkrył. A tymczasem zauważył, że przez nieuwagę naświetliła się pewna płyta fotograficzna… i stąd mamy aparaty rentgenowskie. To długi temat, za długi na ten artykuł.

Jako swego rodzaju perełkę zamieszczę fragment pierwszej strony pracy dwóch Chińczyków. Rzecz jest bardzo aktualna, 2020 rok. Spostrzegli oni, że ciąg liczb trójkątno-kwadratowych jest szczególnym przypadkiem tak zwanych ciągów Horadama (Alwyn Horadam, australijski matematyk, 1923-2016, jego podobizna poniżej). Praca została opublikowana w uznawanym czasopiśmie naukowym. To dowód, że wszędzie jeszcze jest coś do odkrycia.

Czy to odkrycie Chena i Pana znajdzie kiedyś zastosowanie? Nie wiadomo. Być może. Jest pogląd, że cała nauka jest w ogóle "na wszelki wypadek". Żeby "jak co", to uczeni - tak jak wojsko - byli pod ręką. Ale daleko odszedłem od prostej lekcji o matematyce dla młodzieży…

Michał Szurek