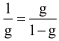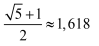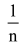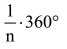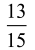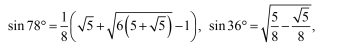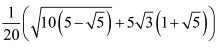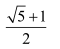Matematyka wokół nas

Ale popatrzmy na zdjęcia, na kilka zdjęć z kilkudziesięciu, jakie zrobiłem w swojej okolicy. Co najpierw rzuca się w oczy? Coraz bardziej skomplikowane symetrie ornamentów. Znalazłem na swoim warszawskim osiedlu czworokąty, pięciokąty, sześciokąty, siedmio-, ośmio-, dziewięcio- dziesięcio-, 11-, 12-, 15-, 16-, 20- i 24-kąty. Poluję na 13-, 17-, 19-. A może Czytelnicy znajdą? Proszę tylko pamiętać, by fotografować tak, żeby nie dało się poznać, czyj to samochód!
Ornamenty te mają wiele odmian, niekiedy bardzo ładnych i ciekawych matematycznie. Najbardziej różnorodne są felgi, mające w sobie pięciokąt foremny (jeszcze dwa przykłady są na fotografiach 7 i 8 - mam oczywiście więcej).
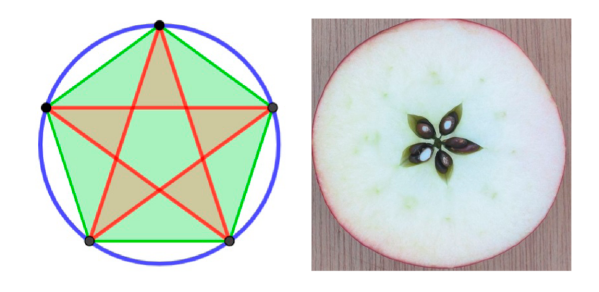
Nic dziwnego - pięciokąt foremny i powstający z niego pentagram (gwiazda pięcioramienna) fascynują nas (=ludzkość) od dwóch i pół tysiąca lat. Występują w sztuce i literaturze. Pełno jest w nim "złotego podziału" - proporcji, która od czasów greckich uchodziła za kanon piękna… aż do dwudziestego wieku, kiedy zaczęliśmy odchodzić od antyku.
Pentagram (gwiazda) był symbolem pitagorejczyków, tak jak ryba symbolem chrześcijan. Nazywany jest różnie. Jedno z nadanych mu określeń w średniowieczu to "klucz Salomona". Na taki klucz chciał Faust w tragedii Goethego zamknąć swoją pracownię przed Mefistofelesem. W pośpiechu narysował gwiazdkę niestarannie i wysłannik Lucyfera przedostał się przez pozostawioną szparę… i wynikło stąd wiele, wiele kłopotów - również dla Małgorzaty. A współcześnie - wiemy, jak dużo państw ma pięcioramienne gwiazdy na swoich flagach. Spójrzmy na rysunek 9 - jabłko to taki smaczny owoc!
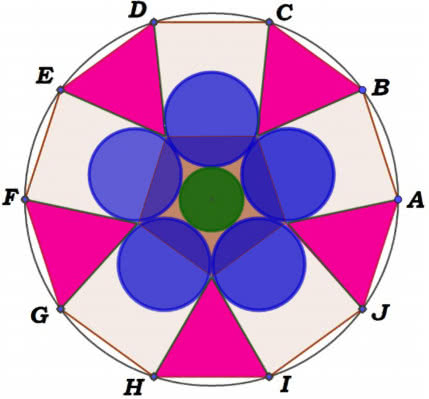
Co widzi matematyk w takich felgach? Potężną geometrię. Porównajmy tę z fotografii 1 i rysunku 10. Deseń nie jest odwzorowany dokładnie, ale patrząc na ten motyw, wymyśliłem zadanie, dość ciekawe z matematycznego punktu widzenia. Mamy dziesięciokąt foremny ABCDEFGHIJ. Pięć dużych kół ma być stycznych do pięciu widocznych trójkątów równobocznych, a małe koło w środku - styczne do pięciu większych. Jak dobrać promienie i środki tych kół?
To wcale nie jest łatwe zadanie. Oczywiście chodzi o rozwiązanie "matematyczne", bo gdybyśmy chcieli wykroić ornament z papieru, tektury czy nawet deseczki - po kilku próbach dopasowalibyśmy wszystko bardzo dobrze.
Zadanie na tyle trudne, że… zajmę się innym, łatwiejszym (!). Spójrzmy znowu na felgę z fotografii 1 i jej inny "model matematyczny" (rysunek 11). Zadanie jest następujące. Szukajmy, jakie rozmiary mają prostokąty ASWP, CDTS, FGWT, IJVW, LVMW - to znaczy, jakie są proporcje ich boków? Czytelnicy, obeznani ze złotym podziałem, postawią być może przypuszczenie, że to są "złote prostokąty". Złoty podział pewnej wielkości na dwie części to taki, że stosunek całości do większej części jest równy stosunkowi większej części do mniejszej. Jeżeli całość oznaczymy przez 1, a większą część przez g, to równaniem złotego podziału będzie
Prowadzi to do równania kwadratowego na g. Obliczamy stąd, że stosunek większej części do mniejszej to
trochę ponad półtora, co jako tako zgadza się z rysunkiem 11. Ale przyjrzyjmy się temu dokładniej.
Mamy oto (rysunek 11) 15-kąt ABCDEFGHIJKLONP.
Jakie ma on kąty? Wyprowadzę najpierw wzór ogólniejszy na kąt wewnętrzny wielokąta foremnego o dowolnej liczbie boków; powiedzmy n. To proste. Kąt środkowy takiego wielokąta to
Pamiętamy, że suma kątów trójkąta to 180°. Tak na marginesie - to odróżnia geometrię euklidesową od innych. W geometrii "eliptycznej" Łobaczewskiego suma miar kątów trójkąta jest mniejsza od 180°, w "hiperbolicznej" geometrii Riemanna - większa. Nie powinniśmy się dziwić, że tak może być.
Na Ziemi trójkąt o dwóch wierzchołkach na równiku, a trzecim na biegunie ma dwa kąty proste (przy równiku) - a więc suma kątów tego trójkąta jest na pewno większa niż 180°. Ale wracamy na… no właśnie, nie na Ziemię, tylko na idealną płaszczyznę Euklidesa.
Popatrzmy na niebieskie figury na rysunku 11, na przykład ABCS. Takie czworokąty to deltoidy. Kąt przy wierzchołku B ma
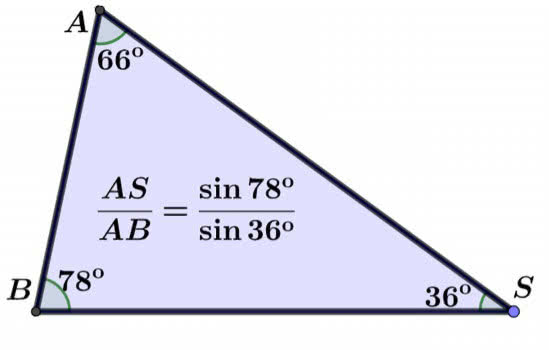
kąta półpełnego, to jest 156°. W wierzchołku S widzimy dwa kąty proste (od prostokątów) i kąt w zielonym pięciokącie wewnętrznym, 108°. Zatem na kąt w wierzchołku S deltoidu przypada 360°-2∙90°-108°=72°. Narysujmy dokładniej trójkąt ABS. Kąt przy wierzchołku B to połowa kąta 156°, czyli 78°. Trzeci kąt ma 66° (rysunek 12). Nie będę przypominał szkolonego twierdzenia sinusów (kto nie pamięta, może wygooglać).
Wróćmy zatem do szkoły. Dawnej. Chodziłem do 41. LO im. Joachima Lelewela w Warszawie. Matematyki uczył mnie Wacław Chyra, przedwojenny inżynier. Dopiero po wielu latach dowiedziałem się, że był bohaterem Powstania Warszawskiego - dowodził plutonem w kilku bohaterskich akcjach. Uczył dobrze. Dziękuję, Panie Profesorze. Sinusy dadzą się obliczyć. Chyba obliczałem to kiedyś na Pana lekcji. Mamy 66=60+36, 78=60+18. Wartości funkcji trygonometrycznych kąta 60° pamiętamy (nie będę przypominał), a dla kątów 18° i 36° można skorzystać z geometrycznych własności pentagramu albo (sprytnie) wykorzystać zależności w trójkącie o kątach 36°=2∙18° i 54°=3∙18°. Otrzymamy wprawdzie równanie stopnia trzeciego, ale da się ono rozwiązać szkolnymi metodami. W każdym razie dało się na lekcjach profesora Chyry.
Ale skorzystajmy z wszystkowiedzącego mędrca XXI wieku, czyli z Internetu. Poprosiłem stosowny program (konkretnie Wolfram Alpha, dostępny bez ograniczeń). Owszem, podał od razu, że
ale z pewną przyjemnością zauważyłem, że nie dał sobie rady z obliczeniem (a raczej: zgrabnym przedstawieniem) ułamka. Wróciłem znów do czasów profesora Chyry i wyliczyłem, pisząc wiecznym piórem na kratkowanej kartce zeszytowej, że ułamek ten upraszcza się do
Potem nawet obliczyłem przybliżoną wartość otrzymanego wyrażenia bez kalkulatora - za pomocą tablic, które każdy musiał mieć na lekcji. Po kilkunastu minutach dostałem odpowiedź: 1,664… Sprawdziłem jednak za pomocą komputera (pół minuty na wklepanie, zero na wykonanie). Zgodziło się! Przypomnę, że złoty podział to proporcja w przybliżeniu 1,618 do 1, a dokładnie
do 1.
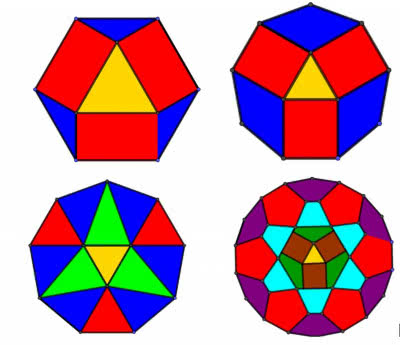
Od jednostkowych zadań-łamigłówek w matematyce bardziej istotna jest ogólność. Na tym polega rozwój nauki, wciąż jeszcze nazywanej Królową Nauk. Co prawda, wszyscy podkreślają, że lot w abstrakcję musi się zaczynać i kończyć konkretem - ale to tak, jak z podróżą samolotem. Tam też latamy ponad chmurami, ale za długo się nie da. Spójrzmy zatem na rozwiązane przed chwilą zadanie bardziej ogólnie. Daję często uczniom i studentom zadanie: "Ułóż zadanie". Tak właśnie. Ułóż. Potem oczywiście rozwiąż. Patrząc na rysunek, dostrzeż go w jak największej ogólności. Jakie wspólne cechy mają ornamenty, które widzisz na rysunku 13?
Podpowiem jedno z możliwych ogólnych zadań. Jaki rozmiar (w stosunku do całej figury) ma środkowy żółty trójkąt w każdej z tych konfiguracji? Proszę spróbować. Jeżeli jesteś, Czytelniku, uczniem - może to ci się przydać na lekcjach w szkole. Spróbuj znaleźć rozwiązanie ogólne. Co to znaczy ogólne? A, na tym też polega zadanie!
Na zakończenie ogólna uwaga. Mam wiele zajęć z uczniami i nauczycielami. Od pewnego czasu nie próbuję wchodzić w zagadnienia współczesnej, trudnej matematyki. Staram się wynajdywać ciekawe, choć elementarne zagadnienia. Ale coraz częściej spotykam się z silnym pragmatyzmem: po co mam się uczyć czegoś, czego nie będzie na maturze? Może to i racja i trochę mi smutno, ale "robię swoje". Czyż geometria felg nie jest ciekawa? A za miesiąc - algebra abstrakcyjna w smartfonie.
Michał Szurek