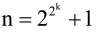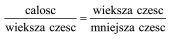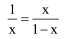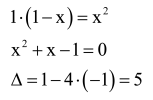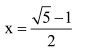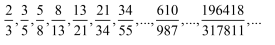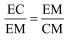Pięciokąt, pentagram, klucz Salomona, pentalpha

Oto ta konstrukcja autora, który nie miał szczęścia zostać w szerokiej pamięci naukowców.
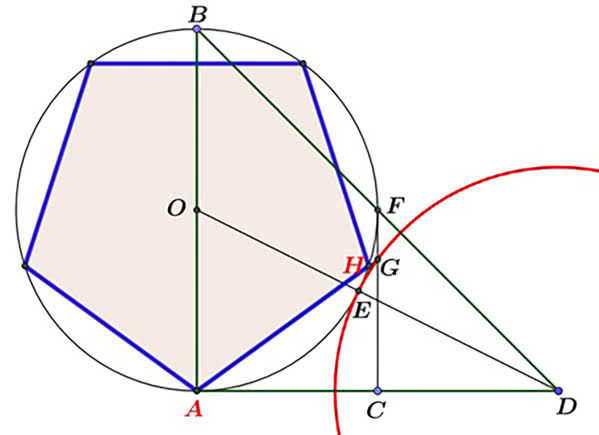
Kreślimy okrąg o środku O i promieniu OA, i średnicy AB. Prowadzimy styczną do okręgu w punkcie A i budujemy trójkąt równoramienny ABD, jak na rysunku 1. Oznaczmy punkty wspólne prostych BO i BD z okręgiem odpowiednio przez E i F. Rysujemy okrąg (wystarczy łuk) o promieniu DE. Niech punktem wspólnym tego okręgu i prostej CF będzie G i niech H będzie punktem wspólnym okręgu i prostej AG. Odcinek AH jest bokiem pięciokąta foremnego wpisanego w okrąg.
Każdy matematyk doceni urok takiego rozwiązania. Można zastanawiać się "jak on na to wpadł?". Ale uczniom w XXI wieku wydać się może dziwne, że w ogóle zajmowano się takimi zagadnieniami, jak coś narysować. Po pierwsze, jeśli już nawet musimy narysować pięciokąt foremny, to bierzemy choćby i najmniej skomplikowany program graficzny Paint. W nim jest stosowna ikonka. A bardziej dokładny rysunek zrobi Geogebra. Kto zaś zna liczby zespolone, ten wiem, że wierzchołki pięciokąta foremnego to pierwiastki równania z5=1. Na równi z popularną już Geogebrą wchodzi też do szkół Wolfram Alpha - bardziej zaawansowany i ogólnie dostępny program do obliczeń algebraicznych - polecam interesujące wprowadzenie Oficyny Wydawnicznej, hm, niech będzie bez kryptoreklamy, Oficyny XY. Oto prezentacja rozwiązania równania z5=1 w liczbach zespolonych w Wolfram Alpha - rysunek 2.
No, właśnie. Zadania "konstrukcyjne" po ponad 2000 lat odeszły do lamusa. Nie chodziło w nich o to, by coś narysować, a "skonstruować" - za pomocą cyrkla i linijki. Wolno rysować tylko odcinki i łuki - co się da, a czego nie da? Wspomnę, że nazywany (już przez współczesnych) "księciem matematyków" niemiecki uczony Karol Gauss (1777-1855) tak się zachwycił własnym odkryciem, jakie wielokąty foremne można tak skonstruować, że postanowił zostać matematykiem - odkrył to bowiem, gdy miał 17 lat! Przedstawiałem to rozumowanie studentom. Jest za skomplikowane, by opisać je tutaj. Sam wynik jest jednak ciekawy. Skupmy się na n-kątach, gdzie n jest liczbą pierwszą. Można skonstruować tylko wielokąty foremne o n bokach, gdzie n jest specjalnej postaci
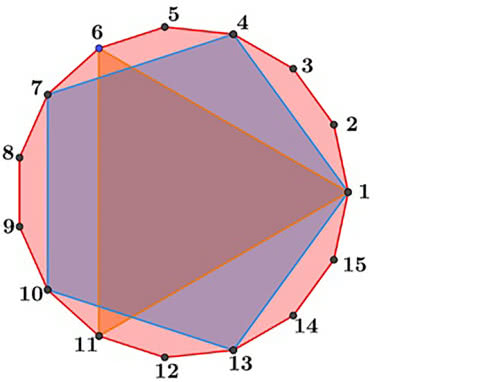
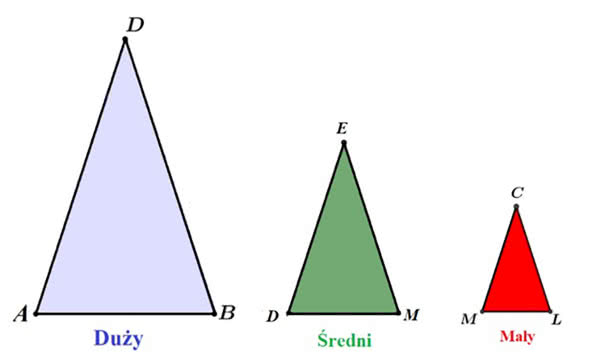
To okazja do powtórzenia sobie działań na potęgach: dla k=0, 1, 2, 3, 4, 5 otrzymujemy kolejno 3, 5, 17, 257, 65537, 4294967297. Nie da się zatem skonstruować ani siedmiokąta, ani dziewięciokąta, ani trzynastokąta. Sześciokąt da się skonstruować z trójkąta, piętnastokąt z trójkąta i pięciokąta (rysunek 3).
Zadania konstrukcyjne były nieco sztuczne. Owszem, ale dobrze uczyły myślenia. Ujmę to szerzej: uczyły pracy z problemem intelektualnym. Od razu jednak powiem, że tego uczymy się na wielu innych zadaniach. Może lepiej, może gorzej. Oczywiście żal mi tego typu zagadnień, którym zawdzięczam miłe chwile w szkole … 60 lat temu. Ale nie jest to wiele ponad naturalne myśli starszego pana, że dawniej było lepiej (tak naprawdę to niekoniecznie).
Pandemia różnie działa na nas wszystkich, ale wśród moich znajomych zaobserwowałem tendencję do zamykania się w sobie, ograniczenia kontaktów - nawet gdy ze względów covidowych można by było. I ja też w centrum miasta bywam raz na miesiąc, a na co dzień sobie chodzę sobie po swojej podmiejskiej okolicy i patrzę, gdzie znajdę coś matematycznego.
Miesiąc temu przypatrywałem się felgom samochodowym - a raczej kołpakom na felgi - i dzisiaj też zacznę od nich. Bardzo często występuje tam motyw pięciokąta i gwiazdy pięcioramiennej. Starszemu pokoleniu nie kojarzy się ona zbyt miło. Turyści lat pięćdziesiątych i sześćdziesiątych pamiętają na pewno szlak tatrzański, z Kuźnic przez Zawrat do Morskiego Oka i dalej do Poronina. Był on znakowany niebiesko, ale z czerwonymi gwiazdkami - bo kiedyś, teraz będzie już przed 110 laty, szedł tamtędy Włodzimierz Iljicz Lenin. Gwiazdki te były pracowicie wydrapywane przez turystów. Nie wiem, dlaczego przypomniało to mi się to, gdy stałem na skrzyżowaniu na czerwonym świetle i zobaczyłem kierunkowskaz stojącej przede mną toyoty. Zdążyłem zrobić zdjęcie.
Od czasów greckich do mniej więcej początków dwudziestego wieku żyliśmy w przekonaniu, że piękno istnieje obiektywnie - że jest pewien jego kanon i tylko nie zawsze umiemy go rozpoznać. Od ponad stu lat patrzymy na to inaczej: jest ono subiektywne. Zależy od kultury, w której się wychowaliśmy i dorastaliśmy. Ale oczywiście nie będę snuć rozważań metafizycznych. Matematycznym wzorcem piękna była ,boska proporcja’, zlaicyzowana potem na ‘złoty podział’. Mamy z nim do czynienia, gdy pewna wielkość tak jest podzielona na dwie części, że
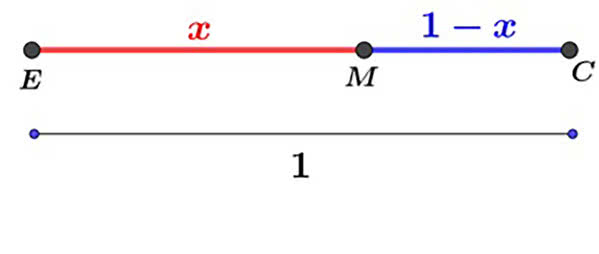
Ujmijmy to matematycznie. Jeżeli całość to 1, a większa część to x, to mamy równanie
Przypomnijmy sobie szkołę:
Ponieważ szukamy tylko dodatniego pierwiastka, mamy rozwiązanie
Nie wygląda to zachęcająco, ale co robić? Właśnie ta liczba wyraża złoty podział, boską proporcję. W zaokrągleniu jest ona równa 0,618, ale bardziej istotne jest, że przybliża ją nieskończony ciąg ułamków:
W licznikach i mianownikach znajdują się tu kolejne liczby Fibonacciego, o których nie będę pisać, żeby za bardzo nie oddalać się od głównego tematu.
Flaga polska ma proporcje 5:8. Nie wątpię, że to z tego powodu: prostokąt o tych wymiarach bardzo zbliża się do ,złotego prostokąta’ - takiego, w którym długości boków są w złotej proporcji.
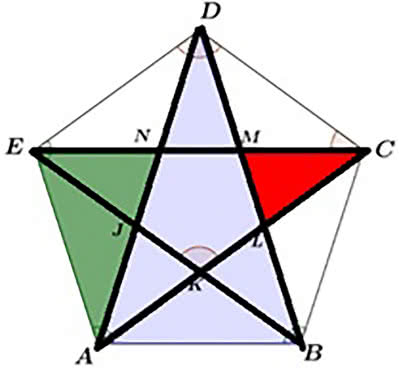
I właśnie ten podział zobaczyli Grecy w pięciokącie i taki ideał harmonii nam narzucili. Taka proporcja zachodzi między bokiem i przekątną pięciokąta. W takim stosunku dzielą się przekątne (na rysunku 3 mamy).
Figura obrosła w symboliczne znaczenie. Regularną pięcioramienną gwiazdę nazywamy pentagramem. Fascynowała pitagorejczyków w VI wieku przed naszą erą. Była ich znakiem, symbolem doskonałości, życia i zdrowia. Rysowali pentagram na piasku jako znak rozpoznawczy, podobnie jak pierwsi chrześcijanie rybę. Co prawda już przed Pitagorasem pentagram miał mistyczne znaczenie.
Babilończycy umieszczali taki znak na pojemnikach z żywnością, żeby się nie psuła. Pierwsi chrześcijanie widzieli w nim symbol pięciu ran Jezusa. Potem poszło gorzej - obecnie dla niektórych jest symbolem szatana. Ale uściślimy - są pentagramy dobre i złe. Ten dobry ("biały") jest zwrócony w górę jednym wierzchołkiem. W złym ("czarnym’) wierzchołek zwrócony jest w dół, a w górę wystają dwa, niby rogi kozła (rysunek 8). Oczywiście wybieramy ten dobry, radosny symbol ogólnoludzki.
Na ilu flagach państwowych on jest, trudno zliczyć. Na większości z nich gwiazda jest "dobrym" pentagramem; na żadnej wierzchołek nie jest skierowany w dół, choć zdarzają się lekko przekrzywione. Na rysunku 9 mamy flagę Panamy. Nielubiany przez połowę kibiców krakowskich klub Wisła Kraków ma jako symbol białą gwiazdę (dla uściślenia: druga połowa kibiców nie lubi Cracovii i spór ciągnie się od ponad 100 lat).
Gwiazda na rysunku 8 ma w prawym dolnym narożniku niedociągnięte linie. Taki sam błąd zrobił Faust. Narysował na progu swojej pracowni "klucz Salomona" - właśnie pentagram, niewpuszczający szatana. Ale Mefistofeles wniknął do środka właśnie przez niedomkniętą linię. Ile szkód potem narobił!
Gdy żył Platon (V-IV wiek p.n.e.) "ludzkość" znała cztery wielościany foremne - cudzysłów postawiłem dlatego, że takimi sprawami interesowała się wąska garstka filozofów. Co prawda Akademia Platońska przetrwała aż do roku 529 naszej ery i została zamknięta decyzją "administracyjną". Cesarz Justynian uznał ją za instytucję pogańską, a więc nieprawomyślną. Tym niemniej uczniowie Platona odkryli piąty wielościan foremny. Jest nim dwunastościan, zbudowany właśnie z pięciokątów foremnych.
Tu mieli nasi filozofowie kłopot. Cztery wielościany pasowały do czterech żywiołów: czworościan - ogień, sześcian - ziemia, ośmiościan - powietrze, dwudziestościan - woda. Co zrobić z piątym wielościanem? Filozofowie od razu znaleźli "odpowiedź": dodekaedr (z greckiego: dwunastościan) to symbol kosmosu, uniwersum, wszechrzeczy, Wszechświata, ładu kosmicznego. Trochę kpiąco zauważę, że podobny kłopot mieli geografowie istniejącego niegdyś państwa o nazwie Związek Radziecki. Najwyższy znany szczyt nazwano imieniem Lenina, aż tu pomiary wykazały, że jest inny, jeszcze wyższy. Co robić? Kto może być wyższy od Lenina? Wybrnięto "po platońsku" - nazwano go Szczytem Komunizmu.
Żarty żartami, a platończycy mieli dobrą intuicję - właśnie dwunastościan pojawia się nieoczekiwanie w różnych działach matematyki. Sam byłem zdziwiony, że w mojej (już byłej) specjalności matematycznej ("wiązki wektorowe") odkryłem go w skomplikowanej konfiguracji tychże wiązek. To było drobne odkrycie i nie przyniosło mi sławy, ale bardzo je lubiłem. Zbieram różne kostki dwunastościenne, a w dowód "sympatii" dla tej bryły sklejałem ją z różnych materiałów i kolorowałem na różne sposoby - co zresztą dawało dobry materiał do zadań matematycznych dla uczniów gimnazjów. Tak, tak, gimnazjów… Na rysunku 10 mamy dwunastościan z pingpongowych, pogrupowanych w cztery układy po pięć w każdym.
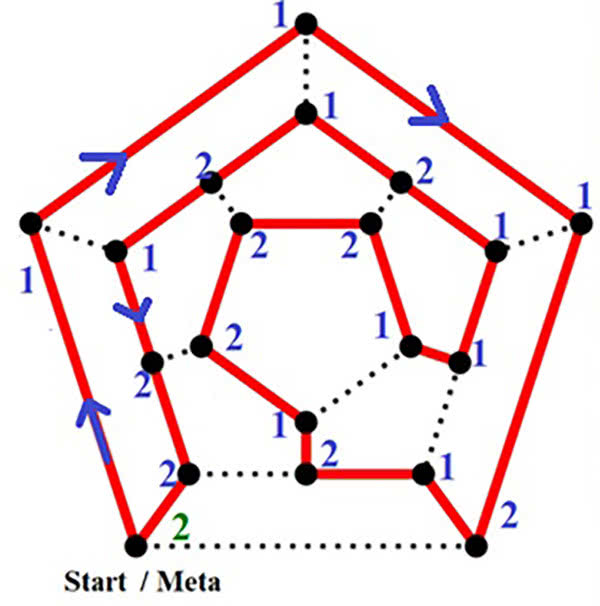
W XIX wieku przez krótki czas (zresztą bardzo krótki) w kręgach intelektualnych modna była zabawa: znajdź cykl Hamiltona na dwunastościanie, czyli objedź wszystkie wierzchołki, jadąc po krawędziach i powróć do punktu wyjścia. Do rozwiązania tej (nietrudnej zresztą) łamigłówki stworzył irlandzki matematyk i fizyk William Rowan Hamilton (1805-1865) całą teorię. Dziś i łamigłówka, i cała teoria wydaje nam się bardzo prosta, ale sto pięćdziesiąt lat temu była to nowatorska konstrukcja, a zagadnienia związane z podróżami po grafach wracają do łask matematyków - z prostych zresztą powodów: optymalizacji przepływów sieciowych. Ale to już inna historia, do której oczywiście wrócę. Dlaczego "oczywiście"? Bo jest ciekawa i ważna we współczesnych zastosowaniach matematyki.
Cyfry oznaczają: 1 - na rozwidleniu wybierz lewą gałąź, 2 - prawą
Michał Szurek