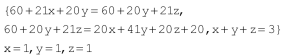Jak (nie dać się) oszukiwać w majestacie matematyki
Albert Einstein nie był pierwszym, który zadziwił się, jak to jest, że matematyka - ten produkt myśli ludzkiej - tak wspaniale pasuje do opisu świata. Na drugim biegunie postawię opinię pewnego ucznia (znalazłem w Internecie): "Nie moja to wina, że matematyka to ogłupianie ludzi za pomocą cyferek".
W tym roku mam jeszcze więcej przykładów, niż do tej pory, ale że zahaczają one o niebezpieczny obszar spraw publicznych, zatem w moim matematycznym kąciku ograniczę się do dawnych sytuacji. Będę zresztą do tych zagadnień od czasu do czasu wracał. Nie pamiętam, kto jest autorem celnego powiedzenia, że liczby są jak ludzie - wystarczy je (ich) pomęczyć, a powiedzą wszystko. Omówię przykłady z trzech obszarów:
- pozornie ścisłe wyliczenia i paradoks Simpsona;
- matematyka a los skazanych;
- matematyka jednak coś wyjaśnia.
Zjawisko 1. Pozornie ścisłe wyliczenia. Zacznę od dyskusji sąsiedzkiej na temat, czy pewne decyzje wpłynęły na podniesienie, czy obniżenie stopy życiowej dwóch typowych polskich rodzin. Przyjmijmy, że są to państwo Malinowscy i państwo Wiśniewscy z Końskich. W ich sklepie osiedlowym bułka kosztowała dwa złote i mleko też dwa złote. Ceny dziś nierealne, ale istota zjawiska nie zależy od tego. Otóż pewnego dnia zmieniło się to nagle: bułka staniała do złotówki, a mleko podrożało do czterech złotych. Sąsiedzi zastanawiają się, czy ogólnie jest podwyżka, czy obniżka. Oddajmy głos zainteresowanym.
Pani Malinowska: Wczoraj za bułkę i mleko płaciłam 2 zł + 2 zł = 4 zł. Dzisiaj płacę 1 zł + 4 zł = 5 zł. Zmiana z 4 na 5 to przecież podwyżka o 1 zł, czyli o 25%
Pani Wiśniewska: Sąsiadko, kto kupuje jedną bułkę do litra mleka? Może tylko dla męża, jak ma kaca? U mnie na litr mleka wychodzi 5 bułek, po jednej dla wszystkich. Wczoraj płaciłam 5∙2 zł + 2 zł = 12 zł. Dzisiaj 5∙1 zł + 4 zł = 9 zł. Czym jest zmiana z 12 na 9? To obniżka o 25%, bo o 3 zł, czyli o jedną czwartą 12.
Pan Malinowski: Rację ma moja żona. Bułka tanieje z 2 na 1, czyli o 50%, mleko drożeje o 100%. Czyli ceny dzisiejsze to (100 + 50)/2 = 125 procent cen wczorajszych. Podwyżka o 25%.
Pan Wiśniewski: Sąsiedzie, mówisz głupstwa. Rację ma moja żona. Przecież na wszystko trzeba patrzeć z perspektywy dnia dzisiejszego. Bułka wczoraj była o 100% droższa niż dzisiaj, a mleko wczoraj było o 50 procent tańsze. Widzimy więc, że ceny wczorajsze to 125% dzisiejszych, a skoro tak, to mamy obniżkę o 25%.
No, to jak jest naprawdę? Odpowiedź jest z pozoru dziwna, ale po chwili namysłu będzie zrozumiała. Nie ma "naprawdę". Różnica zdań między paniami wynika - jak to nazywają ekonomiści - z innej struktury spożycia. Jest oczywiste, że jeżeli państwo Wiśniewscy jedzą dużo bułek, a piją mało mleka, to ważniejsza jest dla nich cena pieczywa. Zilustruję to inaczej: ponieważ ja od 76 lat nie palę papierosów, to dla mnie jest obojętne, ile kosztują. Natomiast spór mężów to mniej więcej paradoks Simpsona, o którym piszę nieco dalej. Obliczanie średnich z procentów na ogół nic nie daje. Są to często obliczenia, które można łatwo wykonać, ale nie mają znaczenia. Nie przekazują żadnej wiedzy. Najlepszym przykładem jest obliczenie średniej arytmetycznej wagi komara i słonia. Można owe liczby dodać, podzielić przez dwa … i co możemy zrobić z tak uzyskaną informacją? Nic. Jest pustą liczbą.
Z nieznajomości procentów przez kuratora oświaty skorzystał kilkanaście lat temu mój znajomy nauczyciel. Było to w Małopolsce. Uczył w kilku klasach z podstawowym programem matematyki oraz w jednej eksperymentalnej - realizował tam program pierwszego roku studiów. Było tam tylko sześcioro uczniów. W pierwszej średnia ocen na maturze (podobno czterdziestu dziewięciu uczniów) wyniosła około 35%. W drugiej cała szóstka dostała około 95%. Kurator dodał, podzielił przez 2 i napisał: "nauczyciel XY ma wybitne zasługi: jego uczniowie osiągają z matury średnio 65%". Mój znajomy nie zdecydował się na zrobienie kuratorowi przyspieszonego kurs arytmetyki.
Znów odwołam się do dawniejszych czasów. Niedługo po wyczekiwanym przez wiele dziesiątków lat wstąpieniu Polski do Wspólnoty Europejskiej (wstąpieniu formalnym, bo w Europie byliśmy zawsze), negocjowaliśmy z Brukselą dotację na budowę autostrad. Coś tam szło jak po gruzie, ale tuż przed końcem 2005 roku udało się; dostaliśmy. I oto 27 grudnia 2005 r. ówczesny premier, Kazimierz Marcinkiewicz, wypowiedział się w Sejmie tak:
Gdybyśmy nie zawarli w Brukseli porozumienia 17 grudnia w sprawie budżetu Unii, nasze wydatki na budowę autostrad musiałyby być o 40 procent wyższe. Można powiedzieć, że zaoszczędziliśmy 40%.
Kazimierz Marcinkiewicz raczej znał się na procentach, ale że w tym momencie był politykiem, więc musiał kłamać. Oj, przepraszam, bardzo przepraszam, uniosłem się, nie wszyscy premierzy kłamią - on po prostu wykorzystał, że znaczna większość ludzi nie dostrzeże naciągania. Zanalizujmy jego wystąpienie.
Co to znaczy, że zaoszczędziliśmy, powiedzmy, 8 złotych? Co to znaczy "zaoszczędzić"? Jeżeli w pubie A za piwo płacę 20 zł, a takie samo piwo w barze B (o równie przyjemnym wnętrzu, równie miłej obsłudze i tak samo sympatycznych klientach) po drugiej stronie ulicy kosztuje 12 zł, to jeżeli przejdę na drugą stronę to nic nie tracąc, zaoszczędzę właśnie 8 zł. Procentowo 8/20, czyli 4/10, czyli 40%.
Wracajmy do premiera Marcinkiewicza. Przyjmijmy - dla prostoty - że budowa kosztowała 140 mln zł, ale dzięki dotacjom unijnym tylko 100 mln poszło z budżetu państwa, a zatem istotnie bez dotacji byłoby o 40% więcej. Zgadza się! Zamiast 140, wydaliśmy o 40 mniej. To ile zaoszczędziliśmy? Tak, jak z piwem: 40/140, czyli 2/7, na procenty jest to mniej więcej 28,5%. To też coś jest, nawet dużo, ale nie czterdzieści!
Ujmę to jeszcze inaczej. Gdyby budowa kosztowała 200 milionów, z czego UE dałaby 100, to czy dałoby się powiedzieć, że zaoszczędzilibyśmy 100%?
Wyjdę na chwilę poza matematykę. Co to naprawdę znaczy "zaoszczędzić". Dowcip sprzed prawie stu lat, przesuszony suchar, ale ujmujący dobrze istotę sprawy. "Tato, zaoszczędziłem 50 groszy, zamiast jechać do szkoły tramwajem, biegłem za nim". "Bardzo dobrze, synku, ale jutro biegnij za taksówką, zaoszczędzisz 5 złotych".
Zagadnienie drugie. Los skazanych zależy od modelu matematycznego. W niemal każdym podręczniku amerykańskim o rachunku prawdopodobieństwa cytowana jest historia rabunku w pewnym sklepie, bodajże w stanie Nebraska. Dokonała tego para:
Afroamerykanin z brodą i kobieta orientalnego pochodzenia. Odjechali żółtą toyotą. W kilkanaście minut później zatrzymała ich policja… No, właśnie, czy ich? Zrabowanych pieniędzy przy nich nie znaleziono, ale sprawa trafiła do sądu. Oskarżeni odpowiadali bowiem rysopisowi: brodaty Afroamerykanin ze skośnooką kobietą w żółtej toyocie. To wszystko. Biegły oszacował prawdopodobieństwo takiej koincydencji na 99 procent i jeszcze z jakimiś dziewiątkami po przecinku. To znaczy rozwiązał zadanie: jakie jest prawdopodobieństwo, że losowo wybrani pasażerowie mają żółtą toyotę i wyglądają tak, jak zeznało wielu świadków. To było dla sądu przekonujące. Zapadł wyrok skazujący. Para nie poddała się jednak, wynajęła lepszego eksperta, który powiedział, że jego poprzednik rozwiązał źle postawione zadanie. Głównie (choć nie tylko) nie chodziło o to, jakie jest prawdopodobieństwo, że istnieje taka charakterystyczna para (a właściwie trójka, bo i samochód miał znaczenie), tylko:
Jakie jest prawdopodobieństwo, że w Nebrasce jest więcej niż jedna kombinacja "Afroamerykanin z brodą, wschodnia kobieta, żółta toyota" przy założeniu, że istnieje co najmniej jedna.
Nawet z samego sformułowania widać, że jest to inne, trudniejsze zadanie. To istotnie skomplikowane i nie będę rozwiązywać. Zwrócę tylko uwagę na to, że los skazanych zależy od przyjęcia takiego czy innego modelu matematycznego. W gruncie rzeczy to smutne, bo przecież jakoś to było. Napadli albo nie napadli.
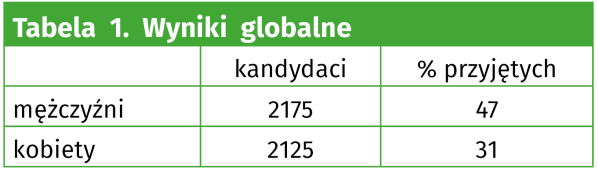
Zagadnienie 3. Paradoks Simpsona. Zdarzyło się to znów w Ameryce, na prestiżowym uniwersytecie w Berkeley w Kalifornii, dokładnie 50 lat temu. Mniej więcej wtedy zaczęła się walka o wyeliminowanie dyskryminacji, głównie ze względu na płeć, ale - jak wiemy, nie tylko. O przyjęcie starało się niemal tyle samo dziewcząt, co chłopców. Minimalna różnica (tabela 1) nie ma znaczenia. Ogólne wyniki rekrutacji były jednak następujące (są to dane autentyczne, ale zawęziłem je do czterech wydziałów, dla większej przejrzystości). Można oczywiście argumentować, że dziewczęta są w ogóle gorsze, ale w to już od dawna nikt w Europie ani w Ameryce nie wierzy, z wyjątkiem Janusza Korwina-Mikke. Zatem zostaje zwykła dyskryminacja i męski szowinizm.
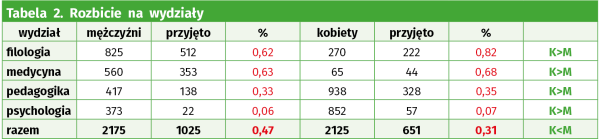
tym duchu zareagowały profesorki w Berkeley i zażądały dymisji rektora. Rozwinięte dane pokazuje następna tabela.
Co widzimy? Na każdy wydział przyjmowano procentowo więcej dziewcząt, a łącznie, na całą uczelnię - chłopców? Jak to możliwe?
To jest właśnie tak zwany paradoks Simpsona. Jak to zrozumieć? Decyduje najbardziej oblegany wydział, reszta ma mniejsze znaczenie. Przejaskrawię dane. Przyjmijmy, że medycyna miała jednak niebywałe większe powodzenie u dziewcząt i że starało się ich czterdzieści razy więcej, czyli 2600. Przyjęto 1760, czyli ten sam odsetek (proszę sprawdzić). W kolumnie M nic się nie zmieniło. W rubryce K mamy 270 + 2600 + 938 + 852 = 4660 kandydatek i 222 + 1760 + 328 + 57 = 2367. Jaki to odsetek?
Nie obliczajmy dokładnie, bo widać, że 2367 to więcej niż połowa 4660.
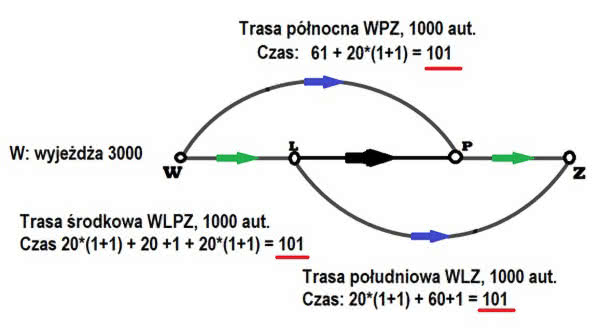
Zagadnienie 4. Matematyka jednak coś wyjaśnia. Lubię paradoks Braessa w ruchu drogowym. Grałem kiedyś w SimCity, nie wiem, czy jeszcze istnieje. Budowało się miasto. Zauważyłem, że często wybudowanie nowej ulicy powiększa korki! No, ale to tylko gra, pomyślałem. Duże było moje zdumienie, gdy dowiedziałem się, że zjawisko to zaobserwowano najpierw w Stuttgarcie, potem w Nowym Jorku i innych miastach. Także odwrotnie: zamknięcie pewnego odcinka drogi w pewnych warunkach poprawiało płynność ruchu. Wyjaśnił to zjawisko matematyk niemiecki Dietrich Braess już w 1968 roku. Zdarza się ono, gdy łączą się drogi lokalne (gdzie szybkość przemieszczania się mocno zależy od liczby pojazdów) z drogami szybkiego ruchu. Oto konkretny przykład. Z miasta W do Z można dostać się dwiema drogami. Pierwsza z nich, północna, to jazda obwodnicą łukiem do węzła prawego (P) na przedmieściach Z i potem zwykłą drogą do centrum Z. Czas przejazdu obwodnicą w minutach to 60 + s, gdzie s jest liczbą pojazdów (w tysiącach). Na drodze dojazdowej czas to 20 s. Co znaczą te liczby? Na obwodnicy wzrost z s = 1 do s = 2 spowalnia ruch o minutę. Na odcinku PZ z 20 minut robi się 40!
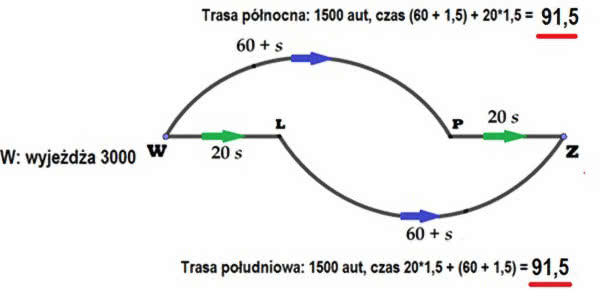
Droga południowa przebiega "symetrycznie", najpierw wyjeżdżamy z W, potem dopiero mkniemy obwodnicą do Z (1).
Weźmy s = 3000. Z miasta W do miasta Z chce dostać się 3000 pojazdów. Można obliczyć, ale łatwo uwierzyć, że optymalnie dla wszystkich będzie, gdy ruch rozłoży się tak samo: połowa trasą północną, połowa trasą południową. Ustali się wtedy tak zwana równowaga Nasha: czas przejazdu to (60 + 1,5) + 201,5 = 91 i pół minuty trasą północną i tyle samo południem: 201,5 +(60 + 1,5)=91,5. "Równowaga" znaczy tyle, że żadnemu kierowcy nie opłaca się zmienić trasy. Jeśli zmieni, to będzie jechał dłużej. Możliwe nawet, że mieszkańcy porozumieli się, kto będzie którędy jeździć. Znam pewien kraj, gdzie by się na pewno nie dogadali.
Dla usprawnienia ruchu wybudowano odcinek LP. Ma on parametry drogi szybkiego ruchu. Czas przejazdu zależy "addytywnie" od liczby pojazdów. To znaczy, że dodaje się, a nie mnoży, a mianowicie wynosi 20+s. Zwiększenie liczby pojazdów o tysiąc to tylko minuta dłużej. "Jak dobrze!", cieszą się mieszkańcy, "ileż to czasu zaoszczędzimy!" Tymczasem…, ale musimy dokonać kilku obliczeń. Wyliczmy równowagę Nasha, przyjmując, że z W wyrusza do Z jak poprzednio, s = 3000 aut, z czego x starą trasą na północ, y na zachód, ale z planem jazdy WLPZ, zaś z najpierw do L, ale potem starą trasą południową, czyli WLZ. Jest jasne, że musi to odciążyć ruch, bo przecież mamy nowy, szybki odcinek.
Obliczmy. Starą drogą północną jedziemy do węzła prawego 60 + x, ale napotykamy tam y wozów jadących z L. Zatem na odcinku PZ wleczemy się aż 20(x+y) minut. Łącznie mamy 21 x + 20 y + 60 minut. Jazda trasą środkową pochłania
20(y+z) + (20+y) + 20(x+y) = 20x + 41y + 20 z + 20 minut.
Starą południową - podobnie jak północną: 20 x + 20y + 60. Równowaga ustala się, gdy wszystkie te czasy są równe. Tak ustaliłoby się i w naturze, gdyby to były przepływy wody, prądu, a nawet megabajtów informacji po komputerowej sieci przewodowej. Poprosiłem o rozwiązanie tego układu równań ogólnie dostępny program Wolfram-Alpha:
Trudno nie zgodzić się z tym wynikiem. Jedna trzecia aut na północ, jedna trzecia środkiem, jedna trzecia na południe. Każdy mieszkaniec miasta W wie, że jeżeli zmieni plan i pojedzie inną trasą, to przedłuży sobie jazdę. Równowaga Nasha. Wszyscy są zadowoleni.
Ejże? Czy naprawdę zadowoleni? Zobaczmy: Pierwsza trasa, północna. Czas 21 x + 20 y + 60 = 21 + 20 + 60 = 101 minut (a było 91,5).
Środkowa: 20x + 41y + 20 z + 20 = 20 + 41 + 20 + 20 = 101. Południowa też 101 minut. "Chcieliśmy dobrze, a wyszło jak zwykle". Przekop się nie udał.
W chwili, gdy to piszę, któraś kolejna fala pandemii przybiera, ale eksperci mają nadzieję - a z nimi my wszyscy - że kolejne będą coraz bardziej łagodne i wreszcie covid da nam spokój. Wprawdzie zostanie z ludzkością na zawsze, ale ileż to chorób wisi w powietrzu… Podobno ludzie pierwotni nie mieli nawet kataru, bo nie było jeszcze odpowiedniego wirusa. Co prawda, nie mam pojęcia, skąd możemy to wiedzieć.
Co to ma wspólnego z matematyką? Po pierwsze, śledziłem prace Centrum Modelowania Matematycznego przy Uniwersytecie Warszawskim. Mieli wyjątkowo trafne prognozy. W mojej porzuconej już działalności naukowej byłem daleki od zastosowań.
Często matematycy szczycą się tym, że latają po przestworzach i nie obchodzi ich to, co na ziemi. Doświadczyłem tego - jest to bardzo przyjemne i daje dużą satysfakcję intelektualną. Spotkałem się też z opiniami inżynierów, którzy po latach pracy na budowie mogą na emeryturze wreszcie zająć się czymś bezużytecznym! Niepotrzebnym, a więc oderwanym od codzienności. Dającym spontaniczną radość.
Od pewnego czasu przybywa jednak i matematyków, których praca jest odpowiedzialna i ważna na co dzień, tu i teraz. Błędy mogą drogo kosztować. Jednym z przykładów jest właśnie tworzenie modeli matematycznych. Zanim coś wdrożymy, powinniśmy prześledzić proces przedtem w teorii, potem - jeśli to wykonalne - na symulatorze. Sprawdzić warianty i ostrożnie wprowadzać, żeby zminimalizować kłopoty. Tłumaczenia, że nie uwzględniliśmy jakiegoś parametru, nie rozwiązują sprawy - system działa źle.
Starożytni Grecy mieli łatwiej. Pytia widziała przyszłość. Czy w XXI wieku widzi ją matematyka? Na szczęście nie.
Michał Szurek