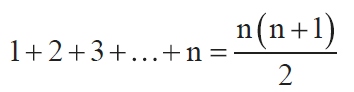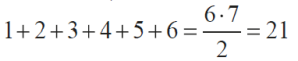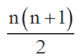Po osi liczbowej
Wiek, w którym się z własnej woli znalazłem (mam na myśli liczbę lat, a nie stulecie), ma trochę zalet, trochę wad. O wadach nie będę pisał, sami zobaczycie. Wymienię jedną z zalet: już "wypada mi" gawędzić tym i owym. Jakie to dawniej równania bywały. Nie takie, co teraz, panie dzieju. Mogę chodzić na spacery, a niekoniecznie na długie wycieczki, wyrypy.
Do rzeczy. Przez najbliższe kilka miesięcy będą właśnie "spacery matematyczne". Nie ukrywam, że z myślą o książce, być może pod tym właśnie tytułem. Jeszcze się przypomnę. Dziś przechadzka pierwsza: oś liczbowa. Na niej tyle się dzieje. Biegnie po niej czas. Biegnie czy płynie? Co to za różnica?
Bieg składa się z pojedynczych kroków, a dokładniej: skoków, a "upływ" kojarzy nam się z ciągłością. Nie możemy sobie wyobrazić czasu, który skacze, gdzie pomiędzy sekundami "nic nie ma". Chyba łatwiej byłoby sobie wyobrazić dyskretność przestrzeni. Termin "dyskretny" znaczy w matematyce mniej więcej to samo, co "skokowy", a słowo to pochodzi od łacińskiego discretus - oddzielony, odosobniony, oddzielny; odpowiednim czasownikiem jest discerne - rozróżniam.
Co to jest ciągłość, co to znaczy? Gubimy się w analizowaniu tego pojęcia, tak bardzo jest ono intuicyjne. Mówimy na co dzień o ciągłych zmianach i ciągłym rozwoju, ale i o ciągłej trosce o przyszłość i niepewności. Obiekt ciągły to nieskończenie podzielny i spoisty. Takie coś nazywamy też continuum, od łacińskiego continere (spajać, zespalać) - stąd kontynent, czyli ląd, który kontynuuje się, w domyśle bez końca i nie rozbija się na oddzielne wyspy. Tak ciągła jest linia prosta - nieskończenie podzielna, a spójna.
Ciągła jest dla naszych zmysłów struktura barw, chociaż dyskretyzujemy ją do różnych palet za pomocą CMYK, RGB i innych skal. Czysty czerwony to RGB (1,0,0) lub FF,0,0 (w zapisie szesnastkowym), lub (0,1,1,0) w palecie CMYK. Ciągły jest dla naszych zmysłów przepływ wody, choć wiemy, że to tylko oddzielne cząsteczki H2O. O, właśnie, czy zastanawiamy się, co jest między tymi cząsteczkami? Powietrze? Ale powietrze to przecież też zbiór atomów i cząsteczek. Widać, że rację miał Immanuel Kant, pruski filozof z Królewca (1724-1804): nie umiemy postrzegać świata inaczej niż przez pryzmat czasu i przestrzeni. W nim i w niej wszystko się dzieje.
Bardzo doceniam trudną prozę Olgi Tokarczuk, w tym Empuzjon, książkę powstałą z zauroczenia Autorki Czarodziejską Górą Tomasza Manna - którą uważa się za powieść o czasie.
***
Tradycyjnie dzielimy matematykę na arytmetykę (dziś: z algebrą) i geometrię (dziś: z trygonometrią). To bardzo stare oddzielenie. Dla Greków były to oddzielne "dyscypliny naukowe" - użycie cudzysłowu przypomina, że to też nowożytne określenie. A jednak są one współzależne i przenikają się wzajemnie.
Pierwszym miejscem, gdzie arytmetyka i geometria spacerują sobie pod rękę, jest właśnie oś liczbowa. Geometryczna linia prosta nie ma początku ani końca, a każdy jej fragment jest nieskończenie podobny do innego. Z drugiej strony, liczby tworzą zbiór, z lekka tylko uładzony relacją mniejszości. I to wszystko.
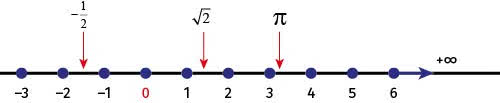
"Nagle gwizd, nagle świst, para buch, koła w ruch. Najpierw powoli, jak żółw ociężale…". Połóżmy liczby na prostej - przeciągnijmy linię prostą przez liczby. I mamy oś liczbową. Na niej są punktoliczby, zwane też liczbopunktami. Uwaga: to moje prywatne określenie - nie jest powszechnie używane!
Przychodzi z pomocą gramatyka. Niech punkt będzie mężem, a liczba żoną. Ich potomstwo zaludnia całą matematykę. Harmonijny związek dwojga. Małżeństwo doskonałe.
Zadanie 1
Startujesz z punktu 0 na osi liczbowej i idziesz krokami "co jeden". Czy dojdziesz do dowolnej liczby? Zakładamy, że oś jest nieskończona, a ty masz nieskończony zapas sił.
Możesz się zdziwić, że w tym jest w ogóle jakiś problem. No pewnie, jeżeli chcę dojść do liczby 2022, muszę wykonać 2022 kroki, a jeżeli do miliona, to milion kroków. Ale to dlatego, że umiemy sobie "jako tako" wyobrazić nieskończoność. Nasz umysł łatwiej pojmie tak zwaną nieskończoność potencjalną niż naprawdę zbiór złożony z nieskończonej liczby elementów. Nieskończoność "potencjalna" to "niekończący się zapas", tak jak z komarami na Mazurach - gdy zabijesz jednego, już leci następny. Ale, zupełnie poważnie, taka potencjalna nieskończoność po raz pierwszy zastanowiła Archimedesa z Syrakuz. Przypomnę: ten grecki uczony, kojarzony raczej z prawem, że ciało zanurzone w wodzie traci pozornie na ciężarze tyle, ile waży woda wyparta przez to ciało, żył w latach 287–212 p.n.e. Według legendy, został zabity przez żołnierza rzymskiego, rozzłoszczonego słowami uczonego, zajętego geometrią: Noli turbare circulos meos. Nie psuj moich kół.
Kilkanaście lat temu znalazłem w Internecie prośbę dziewczyny (może uczennicy, może studentki). Są w nim tak zwane kwantyfikatory - słusznie zapominane w nauce szkolnej.
Anonimowy internauta odpowiedział: Weźmy dwie liczby dodatnie. Zasada Archimedesa mówi, że obojętnie jaka by była liczba y, można ją przekroczyć odpowiednią wielokrotnością liczby x. Podana przez Ciebie wersja jest równoważna. Mówi, że (pomijając już znaki) liczbę y można zawrzeć w dokładnie jednym przedziale postaci [nx, (n+1)x).
Czy mógłby mi ktoś na język polski przetłumaczyć, o co chodzi w zasadzie Archimedesa? Na zajęciach miałam tylko jej postać, ale właściwie nie wiem, do czego ona służy: ∀y ∈ R∀x > 0∃!n ∈ Znx ≤ y < (n + 1)x
Zadanie 2
Ile jest równa suma 1+2+3+…+98+99+100?
To stara historia. Nie wiadomo, czy prawdziwa, ale jeśli nawet nie, to dobrze pomyślana. Karl Friedrich Gauss (1777-1855) był już przez swoich współczesnych nazwany Księciem matematyków. Podobno jego talent objawił się, gdy błyskotliwie rozwiązał zadanie, dane przez nauczyciela, który chciał najwyraźniej mieć spokój na lekcji: obliczcie, ile to jest, gdy doda się wszystkie liczby od 1 do 100. Po kilku minutach Karol miał odpowiedź, a zrobił to tak. Ustawiamy liczby w pary: 1 z 100, 2 z 98, 3 z 98 i tak dalej. Ostatnia będzie para 50–51. Suma liczb w każdej parze to 51; par jest 50; wystarczy pomnożyć 51 przez 50; wynik gotowy: 5050. Można to zrobić "dla dowolnego n", by otrzymać wzór:
Gauss nie pochodził z wyższych klas społecznych; szkoła z anegdotki to zwykła pruska szkoła ludowa. Trzeba docenić i nauczyciela, że nie zbeształ zbyt zdolnego ucznia za to, że zakłócił mu spokój. Nie, nauczyciel polecił chłopca księciu Brunszwiku, a ten "go uczyć kazał". Czy nam się to podoba, czy nie, pomysł szerokiej oświaty ludowej wziął się właśnie z Prus. Nie z altruizmu Fryderyka Wielkiego, o nie. Po prostu ten król pierwszy zrozumiał, że wykształcony żołnierz lepiej strzela.
***
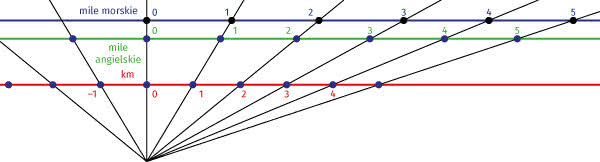
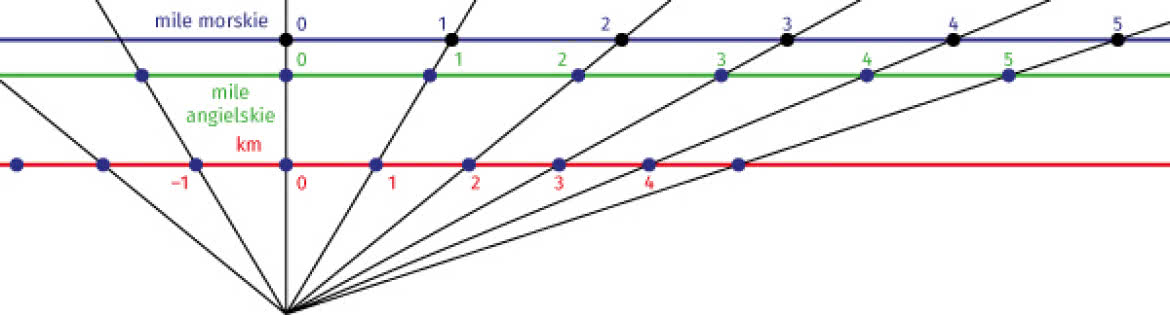
Zobaczmy kilka ciekawych osi liczbowych. Przypomnę, że mila angielska to w przybliżeniu 1609,344 metra. Możemy tę zależność przedstawić graficznie tak jak na rysunku 2. Rzutujemy skalę kilometrową z pewnego punktu. To się nazywa rzutowanie środkowe.
Zadanie 3
Trudniej zmieścić na jednym rysunku kilometry, mile angielskie i mile morskie. Trzeba bowiem precyzyjnie dobrać skale. Czy potrafisz? Mila morska ma 1851,852 metra; możesz przyjąć 1852.
Zadanie 4
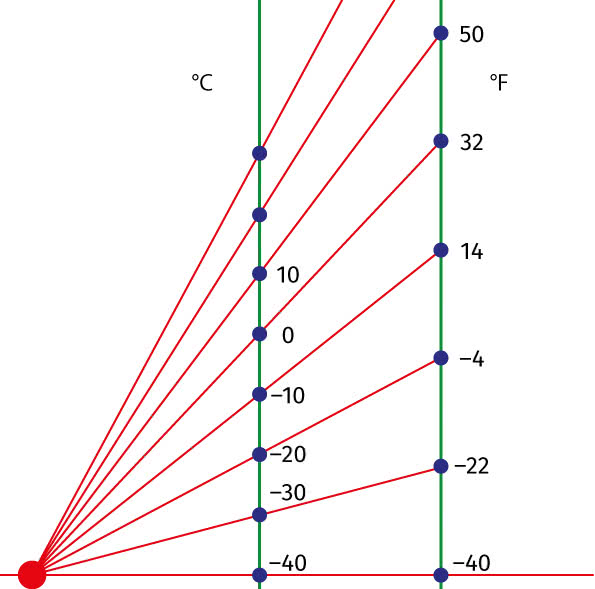
Celsjusz i Fahrenheit. Woda zamarza w 32 stopniach Fahrenheita, a wrze w 212. Jeżeli masz 100 stopni gorączki (oczywiście w stopniach Fahrenheita), to weź aspirynę, ale nie panikuj. Zrób wykres (podobny do tego z milami i kilometrami) o stopniach Celsjusza i Fahrenheita.
W 2035 roku ma być w Europie wprowadzony zakaz sprzedaży samochodów z silnikami spalinowymi. Odejdzie cała epoka, a środowisko trochę odetchnie. Na razie jeszcze możemy rozwiązywać zadania o napełnianiu baku samochodu.
W USA i Kanadzie benzynę sprzedaje się wciąż na galony (choć w Kanadzie od wielu lat obowiązuje system metryczny, a więc i litry). Galony te różnią się - kanadyjski nazywa się imperialnym (wspomnienie Imperium Brytyjskiego!), ten w USA - amerykańskim. Galon imperialny to 8 pint angielskich, czyli 4,546 litra. Galon amerykański to 231 cali sześciennych.
Zadanie 5
Nie zaglądając do Internetu, oblicz, ile litrów ma galon amerykański. Na pewno pamiętasz, że cal to 2,54 cm.
Zadanie 6
Pan Norbert Tremblay, mieszkaniec Montrealu, ma mały samochód, którym na jednym galonie może przejechać 60 mil. Czy można powiedzieć, że ten samochód pali dużo, czy mało?
Zadanie 7
Pitagoras urodził się w roku 572 przed naszą erą. Pomyślmy, ile zdarzyło się od tego czasu. Nie wiadomo zresztą, czy jest to data dokładna, ale przyjmijmy, że tak było. Ile to lat temu? W którym wieku przed naszą erą? Kiedy była/będzie 2600. rocznica jego urodzin?
Zadanie 8
A wy, drodzy Czytelnicy? Czy przeżyliście już miliard sekund? Czy w tym roku szkolnym zrobiłeś/aś już milion kroków?
Zadanie 9
Czy miliard dni temu można było jeszcze (albo: już) spotkać dinozaura? Ile minut temu wyginęły? Możesz powiedzieć, że to pytanie nie ma sensu, bo przecież nie wyginęły w jednej minucie! Tak. Masz rację. A teraz powiem ci, co usłyszałem od pewnej uczennicy: ja lubię matematykę, bo tam mogę kupić 608 arbuzów i nikt nie zapyta, po co mi tyle…
Zadanie 10
Oblicz, ile jest płotków w biegu kobiet na 100 metrów. Od linii startu do pierwszego płotka jest 13 metrów, odległość między płotkami to 8 i pół metra, a od ostatniego płotka do linii mety jest 10 i pół metra. Czy w biegu mężczyzn na 110 metrów jest tyle samo płotków? W tej konkurencji pierwszy płotek jest 13,72 metra od startu, odległość między płotkami to 9,14 metra, a od ostatniego płotka do linii mety jest 14,02 m. Ile jest płotków przy biegu na 400 metrów? Pierwszy płotek jest 45 metrów od startu, potem są rozmieszczone co 35 metrów, a od ostatniego do mety jest 40 metrów. Jak myślisz, dlaczego w biegu mężczyzn są takie dziwne odległości, a w biegu kobiet "normalne".
Zadanie 11
Co to za liczba? W jakiej (praktycznie już zapomnianej) grze towarzyskiej na liczbę tę mówi się "mydło", a w pewnym elitarnym sporcie "miłość" (w oryginale: love)?
Zadanie 12, żartobliwe
Jest rok 1 p.n.e. W Rzymie, w cieniu Koloseum trwają ostatnie przygotowania do powitania nowego roku.
- Marcusie, dokąd idziesz na sylwestra? Przecież to wyjątkowy koniec roku! Jakie szczęście, że żyliśmy przed naszą erą, a od jutra będziemy żyć w naszej erze. Już nie będziemy musieli liczyć lat do tyłu. Zawsze sprawiało mi to trudność.
- Och, Gajusie, jesteśmy z małżonką zaproszeni do Juliusza Cezara. Zamówiliśmy już telefonicznie rydwan czterokonny w Uberze. Gdy zegar wybije dwunastą, zgasimy wszystkie światła - zostawimy tylko lampki na choince i napijemy się szampana.
- A według jakiego czasu wyznaczysz dwunastą? Według czasu Greenwich czy według południka paryskiego? Bo elektronicznego pomiaru czasu jeszcze nie mamy. Wprawdzie Grecy mówili coś o atomach i elektronach, pocierali bursztyn, ale wskazówek zegara tym nie popchną.
- Gajusie, mieszkamy w Romie, a tu mamy czas Greenwich +1. Nawet u Słowian tak jest. Był u nas ich król, Popiel, i mówił, że w Krakowie zawsze o pełnej godzinie grają hejnał z wieży Mariackiej. To ich główny kościół chrześcijański - na pamiątkę najazdu Tatarów.
- Kto to są Tatarzy? Nie słyszałem. Ja spędzę wieczór w rodzinnym gronie. Nie jestem już młody i tańczyć walca ani mazura nie będę. Posłuchamy z żoną klasycznej muzyki - najchętniej średniowiecznej, bo to najbliższa naszym czasom. Nie mamy wprawdzie telewizora, bo ten wynalazek pojawi się za 1950 lat, ale nasi niewolnicy odegrają nam sceny z Boskiej Komedii Dantego. Język włoski Dantego jest dość podobny do naszej łaciny - da się zrozumieć.
- No, to do siego Roku. Wytrop wszystkie niedorzeczności tego dialogu.
Opisz je, wyjaśnij.
***
Na zakończenie spaceru jeszcze inna refleksja o czasie. W starożytnej Grecji czasem rządził Kronos (Chronos, stąd chronometr, chronologia i "chroniczny"). Do Kronosa należał tak zwany dzisiaj czas liniowy, czyli strzałka czasu, ciągły, powolny jego upływ. Powinienem użyć tu czasu teraźniejszego: "należy" - bo przecież bóg nie mógł zniknąć. Był za czasów greckich, jest i teraz, niezależnie przecież, czy w niego wierzymy, czy nie. Ale jest jeszcze Kairos (który w Rzymie stał się boginią Fortuną). Jego atrybutem jest łysa potylica - z jedną tylko grzywką, za którą można go złapać, gdy przechodzi obok. Gdy nie wyczujemy, gdy jest obok nas, kiedy przegapimy ten moment - jest już za późno. Kairos określa czas, ale nie tę rzekę, która jest pod władzą Kronosa, ale czas chwilowy, tę chwilę, która zmienia wszystko. Uchwycenie Kairosa za kosmyk oznacza zmianę, podjęcie decyzji, "złowienie momentu". W retoryce naukowej ma to dwie interpretacje: łucznika i tkacza. Łucznik czeka na odpowiedni moment, by zwolnić cięciwę. Czeka na sprzyjające zewnętrzne okoliczności, "łowi moment". Tkacz musi przesunąć czółenko, gdy wątek i osnowa (pytanie do Czytelników: czy rozumiecie użyte słowa?) znajdą się w specjalnym położeniu, ale sam to organizuje. Podejmuje działanie w ściśle określonym momencie, ale w okolicznościach, które sam przygotował. Sam zwabia Kairosa.
Dlaczego o tym piszę? Mówi łacińska maksyma: carpe diem. Nie znaczy to "gdy jem karpia", tylko "chwytaj dzień". Dostrzeż okazję, stwórz sobie szansę. Powiedzenie to przeniknęło do języków nowożytnych. Wyraża ono przesłanie do młodych Czytelników, może uczniów. Ale właściwie do wszystkich nas. Nie pozwól, by Kairos cię minął. Chwyć go za kosmyk włosów.
Komentarz do zadania 1
Matematycznie - są różne nieskończoności, "mniejsza" i "większa". To odkrycie Georga Cantora (1890 r.) zmieniło paradygmat matematyki. Ale to już inna sprawa.
Komentarz do zadania 2
Możemy efektownie pokazać, że wzór Gaussa jest prawdziwy. Na rysunku 3 widzisz dwie sumy 1+2+3+4+5+6. Dopchnij dolne schodki do górnych. Otrzymasz prostokąt o rozmiarach 6 na 7, a zatem:
Podobne pary schodków można pomyśleć dla dowolnej sumy 1+2+3+...+n i będzie tak samo, to znaczy:
Rozwiązanie zadania 3
Może to być taki rysunek (6).
Rozwiązanie zadania 4
Może to być taki wykres (7).
Rozwiązanie zadania 5
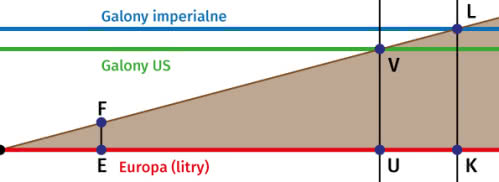
Dwieście trzydzieści jeden cali sześciennych to 231·2,543 cm3, czyli w przybliżeniu 3785,4 cm3. Litr to 1000 cm3, a zatem galon USA to 3,7854 litra. Aby narysować na jednym wykresie zależność między litrami, galonami kanadyjskimi i amerykańskimi, należy dobrać odpowiednio proporcje. Na rysunku 8 proporcje OE:OK:OP=OF:OL:OV mają być równe: 1:3,7854:4,546.
Odpowiedź do zadania 6
Z kontekstu wynika, że pan Norbert mieszka w Kanadzie (w prowincji Québec), używa zatem galonów kanadyjskich. Samochód pana Norberta pali 4,7 litra na 100 km. Obecnie to jest średnia wydajność, hybrydy schodzą już poniżej 4.
Rozwiązanie zadania 7
Zadanie jest proste, ale jest w nim pewien haczyk". W rachubie czasu przyjmujemy, że po roku pierwszym przed naszą erą nastąpił pierwszy rok naszej ery. Podobnie po pierwszym wieku przed naszą erą nastał pierwszy wiek naszej ery. Wieku zerowego nie było. Gdy ustalano chrześcijański system dat, zera "jeszcze nie było" - mam nadzieję, że rozumiesz, dlaczego użyłem cudzysłowu.
"Teraz" znaczy dla mnie rok 2022. Muszę zatem od 2022 odjąć minus 572 - czyli do 2022 dodać 572 i od wyniku odjąć 1. Pitagoras urodził się 2593 lata temu. Było to w szóstym wieku przed naszą erą 2600, rocznica urodzin tego filozofa przypadnie zatem niedługo, już w 2029 roku.
Komentarz do zadania 8
Nie wiem, czy już masz miliard sekund w życiorysie, bo przecież nie wiem, ile masz lat. Sądzę jednak, że od 1 września nie zrobiłeś/aś jeszcze miliona kroków. Czy umiesz oszacować, kiedy to Ci się uda? Dla mojego wieku zaleca się zrobienie dziennie co najmniej 10000.
Komentarz do zadania 9
Jeżeli dowiesz się i zapamiętasz, kiedy i dlaczego wyginęły dinozaury, to i tak będzie pożytek.
Odpowiedź do zadania 10
W każdym biegu jest po 10 płotków. W XIX wieku biegano na dystansie 120 jardów (9,14 m=10 y, 14,02 m=15 y). Dystans zmieniono potem na metryczne 110 metrów. Zmieniono trochę dystans, to pierwszego płotka. Natomiast konkurencja kobiet 100 metrów przez płotki powstała w latach sześćdziesiątych XX wieku (przedtem panie biegały 80 metrów). Wtedy miary metryczne były już w powszechnym użyciu.
Odpowiedź do zadania 11
Jest to zero. "Mydło-mydło" to kamień w grze w domino, na którym nie ma kropek. Natomiast w tenisie na zero (punktów w gemie) mówi się "love". Podobno dlatego, że pewien lord angielski, który lubił tenis, ale grywał bardzo kiepsko, mawiał "och, ja po prostu kocham grać" (Oh, I play just for the love of it). Si non é vero, é ben trovato - tak mówi włoskie przysłowie: Jeśli to nie jest prawdziwe, to dobrze wymyślone.
Komentarz do zadania 12
Sadzę, że to jest świetne zadanie na nowo wprowadzony do szkół przedmiot o nazwie HiT. Łączy historię i teraźniejszość!!! Tam są… same błędy historyczne, większość oczywistych, niektóre nie. To znaczy mam na myśli błędy w zadaniu, gdzieżbym miał przypuszczać, że w podręczniku do HiTu? Wymienię te mniej oczywiste. Na przykład Koloseum zostało wzniesione w latach siedemdziesiątych pierwszego wieku, zatem w jego cieniu nie mogła się odbywać zabawa sylwestrowa. Można też znaleźć powód "fizyczny" - zabawy takie odbywają się w nocy, a więc Słońce nie świeci. Na to można znaleźć kontrargument: a może Księżyc był w pełni?
Ostatni dzień naszego roku to imieniny Sylwestra, stąd nazwa zabawy. Według legendy, pochodzi to wszystko od obaw żyjących wtedy ludzi, że rok 1000 będzie końcem świata. Jakoś tak się nie stało, dopiero obecny rok 2022 daje do myślenia… Papieżem na przełomie "tamtych tysiącleci" był Sylwester II i stąd to wszystko. Ale muszę zrobić dygresję do dygresji. Imię Sylwestra II przybrał Gerbert z Aurillac (żył w latach 945–1003). Zajmował się filozofią, alchemią i matematyką. Nauczał. Nie wiem, czy jeszcze jakiś inny nauczyciel został papieżem…
I jeszcze odniesienie do Cezara - nie dożył "naszej ery" - został zamordowany w idy marcowe w roku minus czterdziestym czwartym. Czyli ile lat po założeniu Rzymu (753 p.n.e.)?
Michał Szurek