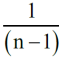Dzielenie i wybory
Najłatwiej dzielić, gdy… się dobrze dzieli. 100 złotych na czterech, piętnaście bułek na pięciu głodnych, sześć sztuk złota dla trójki dzieci i tak dalej. Gdy kwadratową pizzę podzielimy jak na rysunku 1, każdy dostanie taki sam kawałek… Taki sam? No, nie - tylko taki sam pod względem objętości (albo pola powierzchni, bo dla pizzy to to samo).
Ale od razu mamy zadanie: jaka ma być szerokość niebieskiego paska w środku rysunku, żeby istotnie pole było równe jednej trzeciej całości? To nietrudne zadanie.
Ale zastanówmy się. Czy są to naprawdę takie same kawałki? Geometrycznie mają różne kształty, ale to nie wpływa na smak. Tyle, że pizza jest na brzegach trochę przypieczona, a zatem środkowy kawałek jest bardziej treściwy. Czy wobec tego da się podzielić pizzę tak, by każdy dostał tyle samo (w centymetrach kwadratowych) i tyle samo brzegu? Owszem, to nietrudne. Można to zrobić na wiele sposobów, chociaż ten środkowy trudno nazwać praktycznym.
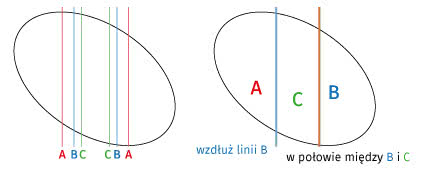
Sytuacja się zmienia, gdy rodzice chcą podzielić kwadratową działkę ziemi między troje dzieci. Owszem, każdy ze sposobów na rysunku drugim ma tę zaletę, że na każdego przypadnie tyle samo brzegu, a więc tyle samo płotu, oddzielającego obszar od zewnętrza. Wydaje się, że pierwszy podział z rysunku 2 jest dobry - kształty nie są takie same, ale podobne. Mogą zacząć się kłótnie, gdy rodzeństwo się trochę posprzecza i każdy będzie chciał odgrodzić się od pozostałych. Płotki wewnętrzne nie będą równej długości.
Ale płotki wewnętrzne to błahostka. Gorzej może być na samym początku. Wyobraźmy sobie, że na południe i na północ od działki są ruchliwe ulice, na północy las, a na zachodniej stronie strumyk. Niech dziećmi będą Andrzej, Barbara i Celina. Jeżeli Andrzej chce mieć warsztat samochodowy na swoje działce, Barbara (dentystka) przychodnię stomatologiczną, a Celina chce mieć… święty spokój, to dojdą do porozumienia. Na prawej części rysunku 2, Celina weźmie część północno-wschodnią (las i rzeczka), a biznesy Andrzeja i Barbary będą się kręcić dobrze, gdy oni wezmą południową i zachodnią (czyli zieloną i niebieską).
Ogólniej rzecz biorąc, łatwo jest dzielić sprawiedliwie rzeczy jednorodne, to jest takie, w których równe części mają równe wartości. Tak mogę podzielić zupę na obiad rodzinny czy jajecznicę na śniadanie. Wróćmy do pizzy. W jednym kawałku pizzy może być więcej oliwek, w innej sera albo szynki. To może być zaletą albo wadą kawałka, który dostaniemy w zależności od tego, co lubimy.
Prosty, a doskonale sprawiedliwy sposób podziału zaproponował Hugo Steinhaus (1888-1972), matematyk lwowski, potem wrocławski. Sposób ten jest właśnie oparty na subiektywnej ocenie części dzielonej całości. Zapewnia, że każdy otrzymuje co najmniej tyle, ile sam uważa za część odpowiednio wielką dla siebie. Co najmniej, ale być może więcej. Jak to jest możliwe, żeby każdy co najmniej tyle, a może więcej niż sam uważa za sprawiedliwą część.
Bardzo prosto. Zwykle tłumaczy się na przykładzie tortu, który trzeba podzielić na n osób. Pierwsza osoba odcina dla siebie jedną n-tą. To znaczy część, którą uważa za jedną n-tą. Każda z następnych osób ma prawo tę część zmniejszyć, jeżeli uważa, że jest za duża. Nóż wędruje do kolejnych osób. Gdy wszyscy już skorzystali z prawa okrojenia tortu, ustalamy, kto ostatni zmniejszył kawałek, to jest odciął z niej choćby drobną część. Tej osobie przypada dany kawałek, już po poprawkach. Łatwo przekonać się, że jest to podział, zapewniający każdemu co najmniej tyle samo, ile by sam chciał. Ostatnia osoba otrzymuje bowiem dokładnie jedną n-tą według własnej oceny całości. Pozostali uważają, że ta osoba wzięła mniej niż jej się należało (skoro odcięła ich subiektywną jedną n-tą), zatem dla nich do podziału jest więcej niż by się należało. Teraz nóż bierze następna osoba i odcina sobie część
Procedura się powtarza; matematyk powie: indukcyjnie, informatyk: rekurencyjnie.
Postępowanie to można traktować jako grę między biesiadnikami. Każdy chce zmaksymalizować swoją wygraną. Gra jest zgodna - graczom opłaca się stosować strategię, która jest optymalna dla każdego z nich z osobna. Ruch na swoją niekorzyść jest natychmiast konsumowany przez współgrających, a próba wyłudzenia nienależnych korzyści spotyka się od razu z ich reakcją.
Z tego opisu widać i ograniczenia sposobu. Z kawałka tortu nie można odkrawać więcej niż kilka razy - zostanie tylko ciapka, może zresztą i smaczna. Mówiąc matematycznie, rzecz do podziału ma być dostatecznie podzielna - jak złoty piasek wykopany przez górników albo kufer ze złotymi monetami, znaleziony przez hrabiego Monte Christo.
***
Postępowanie to można traktować jako grę między biesiadnikami. Każdy chce zmaksymalizować swoją wygraną. Gra jest zgodna - graczom opłaca się stosować strategię, która jest optymalna dla każdego z nich z osobna. Ruch na swoją niekorzyść jest natychmiast konsumowany przez współgrających, a próba wyłudzenia nienależnych korzyści spotyka się od razu z ich reakcją.
Można ten sposób zmodyfikować do ugody kolonistów, który chcą podzielić między siebie nieregularny i niejednorodny obszar. W jednym są lepsze ziemie, w innych gorsze, ale jest lepiej z wodą. Tu jest więcej drzew, tam mniej. Proszą kogoś o przeprowadzenie podziału. Każdy dzieli na mapie obszar na trzy jednakowe części (jednakowe według własnego, subiektywnego odczucia wartości, które może być zupełnie różne dla różnych osób). Jednym warunkiem jest, by linie narysowane były w jednym kierunku, powiedzmy z południa na północ.
Wyobraźmy sobie, że linie biegną tak, jak na rysunku 3. Rozjemca prowadzi dwie linie. Jedną wzdłuż linii podziału B, drugą w połowie podziału CB po prawej stronie. Część lewa (zachodnia) przypadnie A, środkowa C, wschodnia B. Podział ten jest o tyle interesujący, że każdy dostał więcej niż jedną trzecią całości, według własnej, subiektywnej wyceny. Czyż to nie piękne?
Można zarzucić temu sposobowi, że za bardzo zależy od adwokata-rozjemcy, który robi ostateczne kreski na mapie. Ale temu łatwo zaradzić. Należy wprowadzić zasadę, że część położoną najbardziej na zachód bierze ten, czyja linia jest najbardziej na zachód. W wypadku pokrywania się linii rozstrzyga losowanie. Można ten wykazać hojność względem tej pierwszej osoby: najbardziej zachodnią linię rysuje się w poło-wie między dwiema skrajnymi. W ten sposób pierwsza osoba dostaje więcej niż chciała - a pozostałe… też!
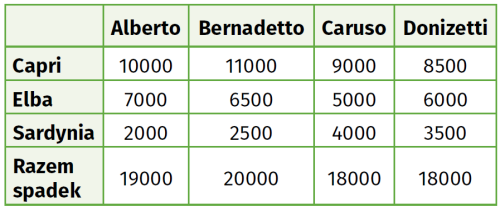
Teraz przykład, kiedy dobra są niepodzielne, a można je podzielić tak, by każdy był zadowolony. Niech oto czterech synów zmarłego szefa mafii: Alberto, Bernadetto, Caruso i Donizetti mają podzielić między siebie trzy posiadłości ojca: jedna na Elbie, druga na Capri, trzecia na Sardynii. Posiadłości nie są warte tyle samo - wszyscy zgadzają się, że najlepsza jest ta na Capri, a sardyńska - to tylko duża ferma. Wszyscy zgadzają się, że posiadłości nie można dzielić, a zatem jeden z braci musi dostać od pozostałych odszkodowanie. Jak przeprowadzić procedurę tak, by uniknąć sporów rodzinnych na następne dwa pokolenia? Należy uwzględnić preferencje rodzinne. Każdy wypisuje własną wycenę posiadłości, powiedzmy w milionach euro:
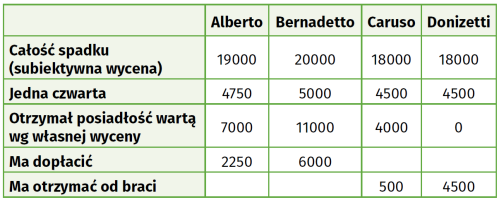
Bracia różnie wyceniają nie tylko poszczególnie posiadłości, ale i całość spadku. Zasada podziału jest sprawiedliwa: każda posiadłość przypada temu, kto ceni ją najbardziej. A zatem Alberto bierze Elbę, Bernadetto swoją ukochaną Capri, a na Sardynii gospodarować będzie Caruso. Ile pieniędzy dostanie Donizetti, najmniej przywiązany do ziemi? Obliczmy:
Alberto i Bernadetto wpłacają do wspólnej kasy odpowiednio po 2250 i 6000. Z tego Caruso bierze 500, a Donizetti 4500. Każdy otrzymał jedną czwartą spadku i to według własnej wyceny… a we wspólnej kasie jest jeszcze 3250 (to znaczy 3 miliony 250 tysięcy euro). Ponieważ bracia są zgodni (jak to w mafii), nie mają problemu z uzgodnieniem, na co wydać te pieniądze.
I to jest pewnym rodzajem gry. Kto chce mieć duże szanse na otrzymanie domu, niech wycenia go jak najwyżej, a pozostałe nisko. Kto woli pieniądze, niech wszystko ceni możliwie wysoko, ale nie za wysoko - tak, żeby być zawsze przelicytowanym. Trzeba też liczyć się z własnymi możliwościami finansowymi. Gdyby Bernadetto wycenił Elbę na 7500, jego ocena spadku wyniosłaby 21000, zatem jego częścią byłoby 5500, a ponieważ zgodnie z regulaminem zabrałby Elbę i Capri, musiałby dopłacić braciom różnicę między 11000 plus 7500 a 5500, czyli 13000.
Aby zapobiec takim sytuacjom, należałoby wprowadzić zasadę, że można otrzymać tylko jedno dobro. Wtedy Elba przypadłaby, jak przedtem, dla Alberto, a Bernadetto za swoją chciwość musiałby wpłacić do wspólnej kasy aż o 250 więcej (jedną czwartą zwiększonej wartości Elby według własnej wyceny).
***
Ale i tu nie jest idealnie. Pewnych dóbr nie da się łatwo przeliczyć na pieniądze. Matematyka się tu poddaje. I bardzo dobrze.
***
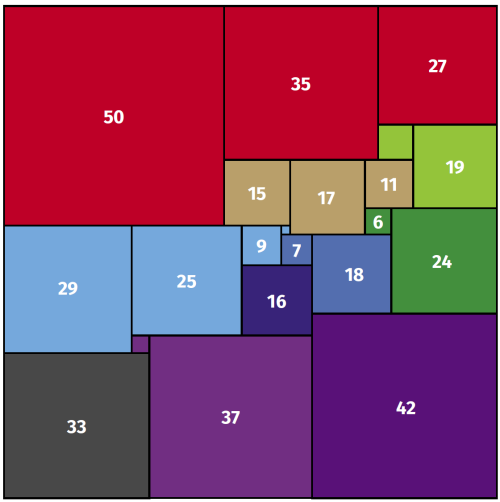
W 1902 roku znany angielski matematyk-amator Henry Dudeney (1857-1930) postawił problem, który nazwał kwadraturą kwadratu (squaring the square). Jest to czytelna aluzja do "kwadratury koła", ale oczywiście chodzi o coś innego, a mianowicie, czy można rozciąć kwadrat na mniejsze kwadraty, ale tak, by każdy wszystkie składowe kwadraciki były różnych rozmiarów. Zadania tego nie rozwiązał. Pierwszym, który podał rozwiązanie "przybliżonego" zadania, był młody lwowski (po wojnie wrocławski) matematyk Zbigniew Moroń (1904-1971). Otóż w 1925 roku opublikował on w czasopiśmie "Przegląd Matematyczny i Fizyczny" artykuł o rozkładach prostokątów na kwadraty. Jednym z wyników był rozkład na kwadraty prostokąta 32 na 33. Dopiero w 1939 r. Roland Percival Sprague znalazł rozkład kwadratu o boku 4205 na 55 różnych kwadratów. W rok później Stone i Tutte zmniejszyli liczbę kwadracików do 28, potem do 24, w 1948 roku Willcocks do 24, a w 1978 r. Adrianus Johannes Wilhelmus Duijvestijn do 21.
Dowód, który przeprowadził Duijvestijn był jednym z pierwszych dowodów trudnych twierdzeń, otrzymanych za pomocą komputera. "Maszyna matematyczna" (tak się wtedy mówiło na komputer), którą włączył Duijvestijn, pracowała całą noc z 21 na 22 marca 1978. Rezultatem było po pierwsze sprawdzenie, że z mniejszej liczby kwadracików niż 21 nie da się złożyć większego. Po drugie, "maszyna" wyrzuciła z siebie również i żądany minimalny rozkład. Oryginalna praca Duijvestijna jest do znalezienia w Internecie (Electronic Computation of Squared Rectangles).
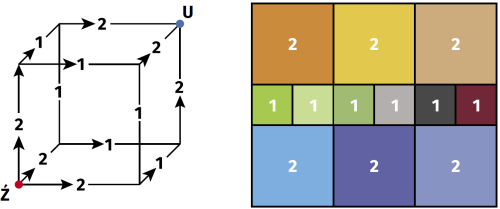
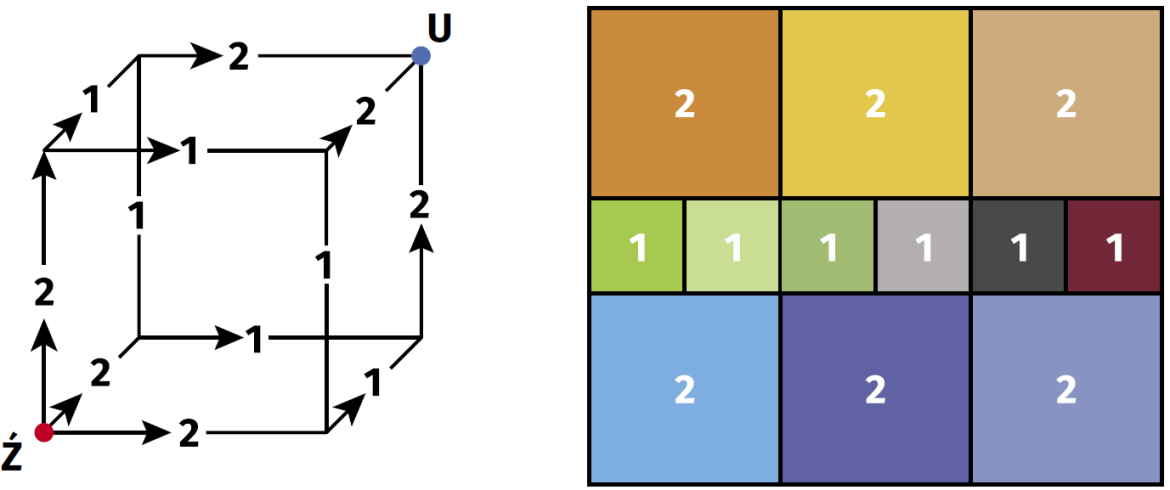
Wbrew pozorom, zadanie nie jest czystą igraszką matematyków. Przekłada się natychmiast na przepływ prądu. Jak? Wyobraźmy sobie, że do górnego i dolnego brzegu kwadratu (ogólniej: prostokąta) podłączony jest prąd i że opór całego kwadratu wynosi R. Jeżeli kwadrat jest pocięty na prostokąty, to opór każdego kawałka jest wprost proporcjonalny do jego długości, a odwrotnie proporcjonalny do jego szerokości. Jeżeli zatem te prostokąty są kwadratami, to ich opór jest taki sam - możemy przyjąć, że jednostkowy. Zatem każdy podział prostokąta na kwadraty generuje sieć elektryczną, złożoną z oporników o oporze 1. Na odrót, taka sieć wyznaczy podział prostokąta. Na rysunku 6 mamy prosty przykład podziału prostokąta, odpowiadający podłączeniu prądu do wierzchołków sześcianu.
prostokąta na kwadraty
***
Jestem w wieku, w którym wolę już nie grać w piłkę nożną. Ale powspominać mogę. Przypomniała mi się zasada, którą ponad sześćdziesiąt lat temu stosowano na moim podwórku, gdy zebraliśmy się (10-14 letni chłopcy) na placu, by pograć w piłkę. Dopiero w wiele lat potem zrozumiałem, że musiał to nam doradzić ktoś dorosły. Może nawet matematyk, bo jest to sposób z teorii gier.
Najpierw wybierano kapitanów, powiedzmy Andrzeja i Janek. Metodą "stópek", której nie opiszę (bo nie jest istotna, taka odmiana rzutu monetą), ustalano, który wybiera pierwszy. Niech to będzie Andrzej. Wskazuje on jednego z nas, powiedzmy mnie (Michał) Wtedy Janek ma wybór. Może wziąć mnie do swojej drużyny albo dać Andrzejowi. Potem Jacek robi to samo: wskazuje kogoś, a Andrzej rozstrzyga przydziale. Spójrzmy, jaki był to psychologiczny majstersztyk. Nie powiem, jakim graczem podwórkowym byłem. Jeśli byłbym dobry, to Jacek wziąłby mnie od razu do siebie, a jeśli patałachem, to zostawiłby Andrzejowi: "po co mi taki, co nie umie piłki kopnąć". I tak szło; po pewnym czasie system się dotarł. Po latach wróciłem do niego, gdy prowadziłem zajęci ze studentami właśnie z teorii gier.
***
I jeszcze jeden sposób wyboru. Będzie o wyborze żony (albo symetrycznie, męża). Pozwolę sobie traktować to binarnie: mężczyzna z kobietą, kobieta z mężczyzną. Oto list do skomputeryzowanego biura matrymonialnego:
"Drogie Biuro. Skojarzył nas Wasz komputer. Dobrał nas idealnie. Mamy te same poglądy na życie i na wychowanie dzieci. Lubimy te same książki, uwielbiamy dokładnie te same potrawy, lubimy spędzać wolny czas w ten sam sposób. Lubimy tę samą muzykę i tych samych ludzi. Jednego tylko nie lubimy: siebie nawzajem".
Michał Szurek