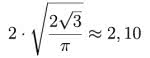Ein Stein, Raz Głaz, one stone, un pierre, una piedra, один камінь
Fizyk Max Born (1882–1970, też noblista: 1954) powiedział później, że ten tom roczników jest „jednym z najwybitniejszych tomów w całej naukowej literaturze. Zawiera trzy artykuły Einsteina, każdy poświęcony innemu zagadnieniu i każdy uznany dzisiaj za arcydzieło”. A co do Maxa Borna, to warto pamiętać, że urodził się i wychował we Wrocławiu. Na domu, w którym mieszkał, umieszczono w 2002 roku tablicę pamiątkową i jego imieniem nazwano jeden z placów Wrocławia.
Albert Einstein jest medialnie znany przede wszystkim jako twórca teorii względności, o której każdy coś słyszał, ale niewielu pojmuje dokładnie, o co chodzi. Jest laureatem Nagrody Nobla (1921), ale nie za teorię względności, lecz za ogólne zasługi dla fizyki teoretycznej i odkrycie praw rządzących efektem fotoelektrycznym. W 1921 roku jego teoria względności została poświadczona eksperymentalnie. Nadano temu, jak byśmy dziś powiedzieli, rozgłos medialny. Było to bowiem zaledwie w trzy lata po wojnie, która wydawała się najstraszliwszą w historii i chętnie wierzono, że wreszcie ludzie poszli po rozum do głowy i teraz zajmować się będą tylko pokojową nauką, harmonią społeczną, rozwojem gospodarczym, rozrywkami i sprawiedliwym życiem. W sto lat potem dzieje się to, co się dzieje…
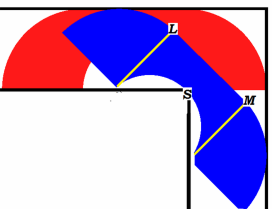
Film Vabank z 1981 roku bawi nas do dzisiaj. Po wyjściu z więzienia, po odsiedzeniu sześcioletniego wyroku, kasiarz Kwinto chce się zemścić na właścicielu banku i ma do tego dobre powody. Aby się włamać do banku, należy wyłączyć nowoczesny, szwajcarski system alarmowy. Zręczny wspólnik konstruuje płytkę specjalnego kształtu, która po włożeniu do aparatu alarmowego wyłącza cały system. Płytka ma niepozorny kształt - na rysunku 1 widzimy kadr z filmu. Jej uszka mają kształt znany w matematyce jako „sofa Hamerslaya” (2). Jest to figura o prawie największym polu, jaką można przesunąć, gdy korytarz zakręca pod kątem prostym. Gdybyś miał, Czytelniku, taki tapczan, nie musiałbyś się martwić przeprowadzki. Dlaczego tylko „prawie największym” polu? Po prostu dlatego, że nie znamy odpowiedzi na tak proste pytanie: jakie jest możliwie największe pole. Odpowiednia liczba, jeszcze nieznana, ma nawet swoją nazwę: „stałą sofy”. Wiadomo, że figura nie może mieć pola większego niż , gdzie s jest szerokością korytarza. Sofa Hamerslaya ma pole 2,2074 s .
Ale artykuł jest o innej „cudownej płytce”, odkrytej w 2022 roku przez matematyka-hobbystę, Davida Smitha. Odkrycie wieńczy 50-letnie poszukiwania „ein steina”. Kto zna język niemiecki, ten wie, że ein Stein znaczy „jeden kamień”. W jednym z opowiadań Stanisława Lema występuje zatem profesor Razgłaz. Matematycy poszukiwali takiego kamyczka od pół wieku. O co chodzi?
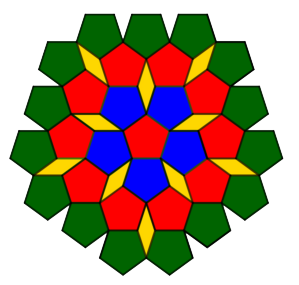
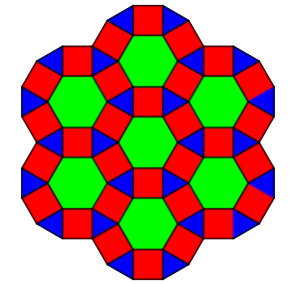
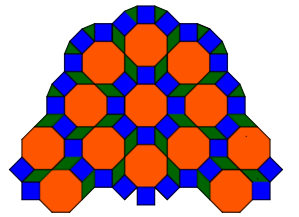
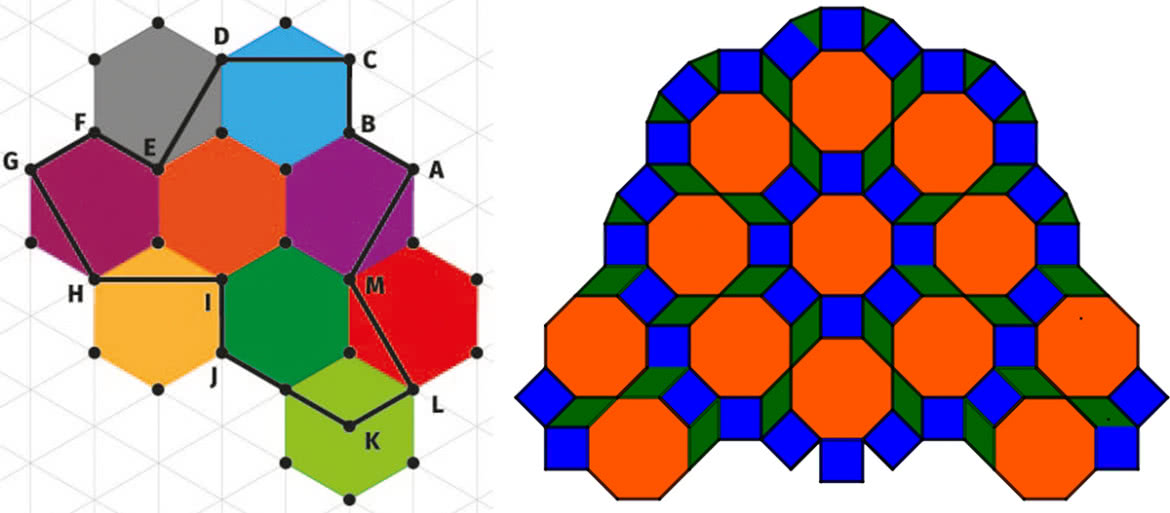
Dużo wiadomo o możliwych układach figur, wypełniających płaską powierzchnię. Można tworzyć najrozmaitsze desenie: ładne, bardzo ładne i piękne. Dawniej chodniki były układane z płyt kwadratowych, a ulice brukowane trylinką: kostkami sześciokątnymi. Dziś króluje kostka Bauma, na podłodze mamy na ogół prostokąty, ale w salach balowych możemy mieć najrozmaitsze ornamenty. Umiemy je klasyfikować. Jest w nich zawsze pewna powtarzalność, symetria, matematyczna regularność. Spójrzmy na rysunki 3…5. Piękno tych deseni polega właśnie na symetrii.
Trójwymiarowe „ornamenty” to sieci krystaliczne. Dają matematyczny opis struktury kryształu. Na mineralogii się nie znam, ale podobno z geometrycznego kształtu kryształu można wyprowadzić niektóre własności fizyczne i chemiczne minerału (proszę sprostowanie, jeżeli to nieprawda).
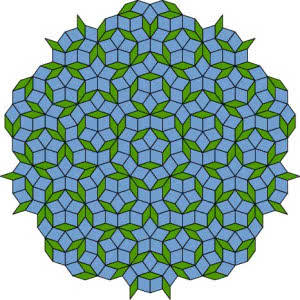
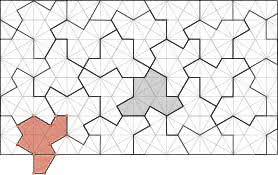
Napisałem, że w takich deseniach i ornamentach jest pewna symetria i cykliczność. Otóż... wcale nie i właśnie o to chodzi. Poszukiwania niekresowego wypełnienia płaszczyzny trwały od lat pięćdziesiątych XX wieku. W 1966 roku Robert Berger podał przykład nieokresowego wypełnienia płaszczyzny - za pomocą 20426 kafelków (tak, ponad 20 tysięcy). Potem zmniejszano liczbę kafel-ków, a dużo hałasu wywołało odkrycie Rogera Penrose’a – pokrycia nieokresowego za pomocą dwóch rodzajów wielokątów (1973). To było dość medialne odkrycie: każdy może na własne oczy zobaczyć kafelki Penrose’a (6). Zostały wykorzystane w niezliczonych deseniach, nadrukach, afiszach reklamowych. Nie wiem, czy autor opatentował pomysł. Pewnie tak.
Jak napisałem, matematyk-hobbysta o dość typowym imieniu i nazwisku, David Smith, odkrył, że do wypełnienia płaszczyzny wystarczy jeden, niepozorny wielokąt. Nie był pewny, czy ma rację. Poprosił o pomoc trzech matematyków, którzy zawodowo zajmują się geometrią (Craig S. Kaplan, Joseph S. Myers i Chaim Goodman-Strauss) i tak w marcu 2023 ukazał się ich wspólny preprint, w którym odkrycie Smitha zostało należycie udowodnione. Dlaczego „preprint”? Aby artykuł mógł być opublikowany w uznanym czasopiśmie naukowym, wszystko trzeba sprawdzić. To może zająć trochę czasu, bo dowód nie jest prosty. Dopiero po opublikowaniu w takim czasopiśmie twierdzenie zostanie uznane przez świat matematyczny. Sprawa znów jest medialna, gazety codzienne i Internet przynoszą jak zwykle dużo fakenewsów, jakoby „coś się nie zgadzało”. Poczekamy, zobaczymy.
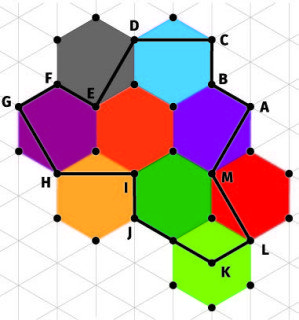
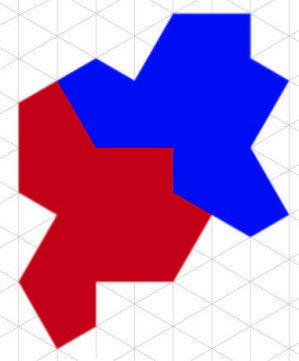
Odkryty przez Davida Smitha kształt to wielokąt o 13 bokach, o nieskomplikowanych kątach (7). Są właściwie dwa takie wielokąty - jeden z nich jest lustrzanym odbiciem drugiego (8). Zbadajmy ich proste własności.
Zadanie
Wyznacz kąty, obwód i pole wielokąta ABCDEFGHIJKLM na rysunku 7. Jednostką jest długość jednego odcinka siatki trójkątnej.
Rozwiązanie
To nietrudne zadanie. Mamy cztery kąty proste (w wierzchołkach A, C, G, L), pięć kątów rozwartych po 120 stopni w wierzchołkach D, F, H, J, K, dwa wklęsłe po 240 stopni w wierzchołkach B, M i dwa kąty wklęsłe po 270 stopni w wierzchołkach E, I. Sprawdźmy, czy się zgadza. Suma kątów każdego wielokąta o n bokach to 180·(n–2) stopni. Dla trójkąta to 180°, dla kwadratu 360°, a dla 13-kąta powinno być 1980°. Zgadza się: 4·90+5·120+2·240+2·270=1980
Kąty pomogą nam odróżnić dwie wersje ein steina. Spójrzmy na kąty proste (w wierzchołkach A, C, G, L) na rysunku 7. Łamana MAB ma kształt litery L (tylko obróconej). Łamane BCD, FGH, KLM to już nie litery L, tylko ich odbicia lustrzane (a więc greckie Γ). Mamy zatem jedną L i trzy Γ. W drugiej, symetrycznej wersji figury mam na odwrót: trzy L i jedną Γ.
Obliczmy długość obwodu naszej płytki. Mamy sześć odcinków długości 1, a mianowicie AB, BC, EF, FG, IJ, KL, jeden odcinek JK długości 2, ponadto 6 odcinków CD, DE, GH, HI, LM, MA długości. Łącznie to:
8 + 6√3 ≈ 18,39
Nietrudno obliczyć i pole naszej figury. Najprościej będzie policzyć, ile zmieści się w niej oczek trójkątnych. Okazuje się, że 32. Pole trójkąta równobocznego o boku a to
a zatem pole naszej figury to 8√3 . Koło o takim polu ma promień:
Rysunek 9 pokazuje nieregularne i nieokresowe pokrycie płaszczyzny jednym kafelkiem. Jednym? Można się spierać, czy naprawdę jednym. Otóż „od czasu do czasu” trzeba użyć lustrzanego kafelka. Zaznaczone na rysunku 9 wielokąty nie są takie same - jeden z nich jest odbiciem drugiego, jest przewrócony na drugą stronę. Nie wiemy, czy zawsze tak trzeba - czy może jest pokrycie bez używania odbicia lustrzanego. Tak, czy owak, wynik jest ciekawy i można się zdziwić, że został znaleziony przez matematyka-hobbystę po pół wieku poszukiwań przez „zawodowców”.
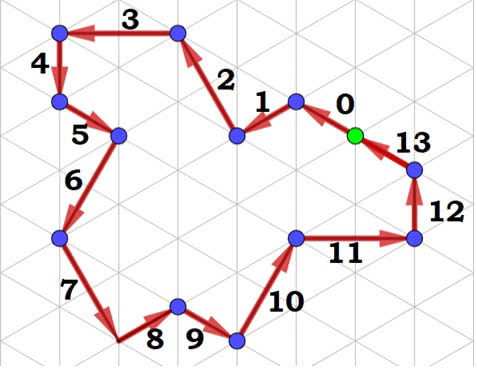
Jak narysować ein steina za pomocą gps? Dawniej nazywało się to „metodą żółwia”. Wybierz dowolnie punkt startowy na siatce. Każdy krok wykonujesz (= rysujesz linię) aż do napotkania węzła siatki.
0. Idź prosto.
1. W lewo 60 stopni.
2. Pod kątem prostym w prawo.
3. W lewo 60 stopni.
4. Kąt prosty w lewo.
5. 60 stopni w lewo.
6. Kąt prosty w prawo.
7. 60 stopni w lewo.
8. Kąt prosty w lewo.
9. 60 stopni w prawo.
10. Kąt prosty w lewo.
11. 60 stopni w prawo.
12. Kąt prosty w lewo.
13. 60 stopni lewo. Jesteś na miejscu.
Spora część Czytelników zadaje sobie na pewno pytanie: „po co to wszystko. Komu potrzebne są takie odkrycia?” Po pierwsze: matematyka ma coś wspólnego ze sztuką, a mało kto zadaje sobie pytanie, po co istnieje malarstwo, rzeźba i muzyka. Po drugie: choć mało wiem na ten temat, to podobno jednak przyda się w krystalografii. Po trzecie i najważniejsze: z odkryciami matematycznymi jakoś tak jest: nagle się przydają. Nagle komuś przychodzi do głowy: ojej, zastosujmy tę ciekawą matematykę. Ale i sama matematyka się zmienia pod wpływem zastosowań. To już temat na inny artykuł. Miłych wakacji.
Michał Szurek