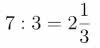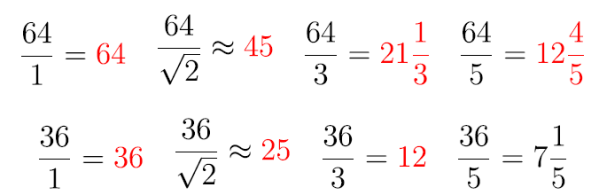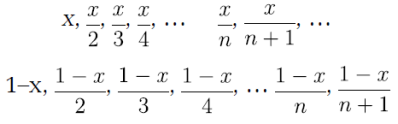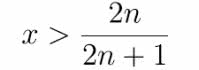Październikowe równania
W mediach pisze się i mówi o wyborach od długiego czasu. Jest to jeden z głównych tematów dla dziennikarzy - w tym i metoda liczenia głosów. Dokładniej: nie tyle samego przeliczania, lecz zamiany wyników głosowania na konkretny przydział mandatów. I o tym jest ten artykuł, być może dublujący kilka innych, z innych tygodników i miesięczników. Oczywiście będzie tylko o matematyce.Pierwszą algorytmiczną metodę elekcji kandydatów na podstawie liczby oddanych głosów w demokratycznych wyborach opracował geodeta i oficer armii duńskiej Carl Andrae (1812–1893). Zastosowano ją w wyborach w Danii w 1855 roku, kiedy Andrae był ministrem finansów. Metoda jest ciekawa i właśnie konkretna, algorytmiczna. W XIX wieku była bardzo czasochłonna. Dziś tych problemów już nie ma - rozwiązałby je prosty program komputerowy. Omówię na nieco abstrakcyjnym i ahistorycznym przykładzie. Siedmiosobowa komisja uniwersytetu w Pireusie ma wybrać trzech spośród sześciu zgłoszonych kandydatów do Greckiej Akademii Nauk: Arystoteles, Euklides, Pitagoras, Platon, Sokrates, Tales. Każdy z członków komisji wypisuje nazwiska w kolejności swych preferencji. Załóżmy, że układają się one tak.
W metodzie Carla Andrae karty się mieszało i potem wyciągało w losowej kolejności. Dla uproszczenia załóżmy, że zostały wylosowane w tej właśnie kolejności.
Liczbę głosujących dzielimy przez liczbę kandydatów, których mamy wybrać i odrzucamy część ułamkową. Ta liczba nazywa się u Andrae podstawą wyboru. W podanym przeze mnie przykładzie mamy
a zatem podstawą wyboru jest liczba 2.
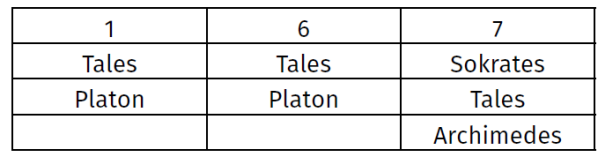
Z kolejnych list odczytujemy nazwisko najwyżej wymienionego kandydata. Przerywamy odczytywanie, gdy ktoś osiągnie podstawę wyboru. W naszym przypadku: gdy jego nazwisko zostanie wymienione dwa razy. Mamy kolejno: Tales, Arystoteles, Euklides, Arystoteles. STOP. Panie profesorze Arystoteles: gratulujemy - został pan wybrany do Aeropagu Greckiej Starożytnej Akademii Nauk.
Karty, które posłużyły do wyboru Arystotelesa (a więc nr 2 i 4), odkładane są na bok. W dalszym postępowaniu biorą udział karty 1, 3, 5, 6, 7 z tym, że skreśla się z nich nazwiska już wybranego kandydata (Arystotelesa). Znów losujemy kolejność odczytywania kart i znowu założę, że jest właśnie taka, jak napisałem.
Czytamy nazwiska, które są na czele poszczególnych list: Tales, Euklides, Euklides. STOP. Gratulujemy, panie docencie Euklides.
Usuwamy zatem karty 3 i 5, dzięki którym awansował Euklides. Usuwamy jego nazwisko z pozostałych. Zostają karty nr 1, 6, 7 z takim nazwiskami:
I oczywiście przechodzi doktor habilitowany Tales.
Metoda ciekawa, ale zwróćmy od razu uwagę na jej wadę. Tales pojawia się tylko na trzech listach, ale to on przechodzi, a nie właśnie Sokrates z Aten (469–399), uznawany za największego mędrca Starożytności, mąż Ksantypy - który był na czterech. Miał pecha, że cztery razy był drugi za kandydatem wygrywającym kolejną turę. Nie ma idealnego systemu, a nawet można wykazać, że nie może go być (tzw. twierdzenie Arrowa o niemożności). Poza tym można łatwo wpaść w tak zwany paradoks Concordeta. Można ten paradoks łatwo opisać. Przyjmijmy, że wyborcy z równą częstością wybierają trzy warianty kolejności: A>B>C, B>C>A i C>A>B. Wtedy mamy pat, bo :13.
wyborców uważa, że A jest lepszy niż B i jednocześnie wyborców uważa, że B jest lepszy niż C i jednocześnie wyborców uważa, że C jest lepszy niż A.
***
Tyle o pomyśle Carla Andrae. Przypomnę: był to pierwszy sposób nowoczesnego liczenia głosów, tzw. SVT, single transferable vote. Najbardziej znaną dziś metodę SVT zaproponował belgijski prawnik i matematyk Victor d’Hondt (1841–1901). Poprawiano ją wiele razy, a jedna z wersji m.in. tzw. zmodyfikowana metoda Sainte-Laguë była zastosowana w Polsce w wyborach parlamentarnych w 2001 roku oraz w wyborach do rad gminnych (dla gmin o ponad 20 tysiącach mieszkańców) w 1990 i 1994 roku. W dalszej części artykułu wyjaśniam to bardziej szczegółowo.
***
Przejdźmy do wyborów powszechnych. W ogóle w czym problem? W Konstytucji naszej Ojczyzny jest podane, że wybory mają być… ogólnie rzecz biorąc, sprawiedliwe. Wystarczy przecież stosować się do ustawy zasadniczej. Ale co to znaczy? Sprawiedliwość jest dość mglistym pojęciem, a „diabeł tkwi w szczegółach”. Oto pierwszy przykład.
W pewnym okręgu, mającym sto tysięcy wyborców, głosy na partie A, B, C, D ułożyły się tak: 40 tysięcy na A, 30 na B, 20 na C i 10 na D. Gdyby było 10 mandatów do obsadzenia, moglibyśmy się zgodzić na podział: cztery na A, trzy na B, dwa na C i jeden na D. Ale co robić, gdy mandatów jest sześć?
Sposób 1. Zwycięzca bierze wszystko; sześć miejsc na partię A. Tak jest w wyborach prezydenckich w USA: zwycięzca w poszczególnym stanie dostaje głosy wszystkich elektorów z tego stanu.
Sposób 2, logiczny, proporcjonalny. Mnożymy procenty głosów przez 6: dostajemy kolejno:
0,4·5=2,4, 0,3·6=1,8, 0,2·6=1,2, 0,1·6=0,6
i najpierw patrzmy na części całkowite (przed przecinkiem). Przydzielamy dwa mandaty dla partii A, jeden mandat dla B, jeden dla C. Zostają dwa. Patrzymy na części ułamkowe. Najwyższe mają partie B i D. Miejsca w parlamencie rozdzielone są tak: 2–2–1–1. Można dyskutować, czy to sprawiedliwie.
O, właśnie, Metoda, którą tu opisałem, jest najprostsza, najbardziej zrozumiała, najbardziej logiczna i bardzo geometryczna, o czym niżej. Nazywa się ona współcześnie „metodą Hareya–Niemayera”, ale była znana od zawsze. Ściślej: od czasu, kiedy zaczęły się takie demokratyczne wybory. To częste w matematyce, a ogólniej w nauce i w życiu, że nazwa pojęcia, wynalazku, odkrycia, nie pochodzi od rzeczywistego autora.
W Polsce zastosowano tę metodę w wyborach do Sejmu w 1991 roku. Potem bardzo ją krytykowano; a mianowicie, że wskutek tego weszło do Sejmu za dużo drobnych partii i było potem trudno się dogadać i że to podobno źle. Ja mam swoje zdanie na ten temat: zamiast mozaiki mamy dwa duże stronnictwa i widzimy, co się dzieje. Ale to nie wina matematyki. Już John Stuart Mill (angielski filozof, 1806–1873) postulował właśnie odejście od systemu większościowego na korzyść proporcjonalnego. Miał na to argumenty z „naszych czasów”: demokratycznie wybrana większość ma tendencję do nieszanowania mniejszości, w tym małych grup.
Nie pamiętam, czy w następnych polskich wyborach zastosowano już tak zwaną zasadę d’Hondta, czy jedną z zasad dość podobnych. W tegorocznych (2023) wyborach, jak i w poprzednich, obowiązuje ten „klasyczny d’Hondt”. Na czym to polega?
Będę się trzymać powyższego przykładu. Dzielimy liczby otrzymanych głosów przez kolejne liczby 1, 2, 3, 4, i tak dalej. Dla partii A będą to liczby 40, 20, 13, 10. Dla partii B: 30, 15, 10, 7,5. Dla partii C będzie to 20, 10, 6,7 i 5; a dla najmniejszej partii D to liczby 10, 5 i jeszcze mniejsze. Wybieramy sześć najwięk-szych liczb. Miejsca w parlamencie są rozdzielone tak: 3–2–1–0. Mała partia D znika, kosztem największej A. O to właśnie chodziło - a czy słusznie, czy nie, to inna sprawa.
***
Bodaj najlepszą metodą byłaby ta oparta na… geometrii wielowymiarowej. To jednak jest (niestety) do-tatecznym powodem, żeby jej nie wprowadzać. Ale metoda jest ciekawa i matematycznie najlepsza. Opisał ją Hugo Steinhaus w swojej słynnej książce Kalejdoskop Matematyczny. Chodzi o to, co zawsze: żeby danemu rozkładowi głosów odpowiadał najbliższy możliwy rozkład mandatów i jak zawsze, sprawa rozbija się o to, co znaczy „najbliższy możliwy”. Sprawę rozwiązuje geometria. Wiemy, że najkrótszą drogą łączącą dwa punkty jest odcinek. Na początek wróćmy do arytmetyki.
Dla uproszczenia przyjmijmy, że są dwie partie: Postępowi Konserwatyści (w skrócie PK) i Konserwatywni Postępowcy (w skrócie KP). W okręgu wyborczym nr 73 oddano 100 tysięcy ważnych głosów, w tym 64 tysiące na PK i 36 na KP. Przyjmijmy teraz, że w okręgu jest osiem mandatów. Jak je podzielić?
Przypomnę zatem metodę proporcjonalną. Mnożymy frakcje oddanych głosów przez 8. Mamy:
PK: 0,64·8=5,12; KP=0,36·8=2,88
Gdyby to były pieniądze, np. 800 złotych, to sprawa była by jasna: PK dostaje 512 złotych, KP 288 złotych. Ale miejsca w parlamencie nie są ułamkowe. Jest jasne, że PK powinno dostać 5 miejsc (bo ma wynik „5 z hakiem”), KP 2 miejsca, ale komu dać ósme? Porównujemy części ułamkowe. Większą ma KP (88 setnych), więc im przypada ósme miejsce. Wynik: 5–3. Stosunek głosów wyborców 64:36, czyli w przybliżeniu 1,78 dał stosunek mandatów 1,66. To bardzo dobre przybliżenie.
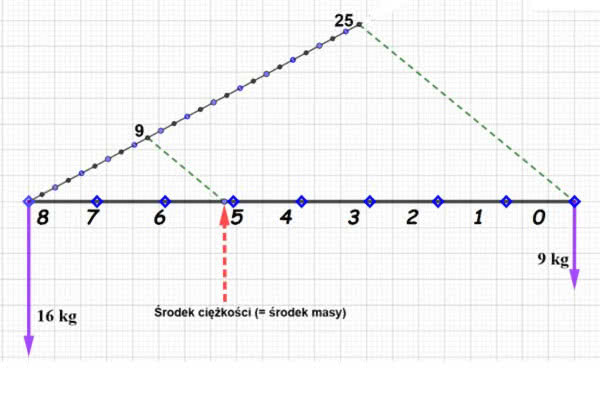
Jak wspomniałem, metoda ta jest najbardziej sprawiedliwa; można ją nazwać „parytetową”. Pochodzi - i to jest właśnie najciekawsze - z geometrii i fizyki. Belkę (kijek, patyk, drąg, odcinek) dzielimy na części, jak na rys. W końcach odcinka zawieszamy ciężarki wagach proporcjonalnych do liczby oddanych głosów. Środek ciężkości wskazuje, ile mandatów przypada każdej z partii. Znajduje się on najbliżej punktu 5. To znaczy, że PK dostaje 5 mandatów, a reszta (a więc 3) przypada KP. Przypomnę, jak się wyznacza środek ciężkości geometrycznie. Rysunek 1 wystarcza za całe objaśnienie.
Interesujące rzeczy „dzieją się”, gdy mandatów jest siedem. Znów zacznijmy od metody proporcjonalnej. Mnożymy procenty przez 7. Mamy:
PK: 0,64·7=4,48; KP=0,36·7=2,52
Porównujemy części ułamkowe. Większą ma KP (52 setne), więc im przypada siódme miejsce. Wynik: 4–3. Stosunek głosów wyborców 64:36, czyli w przybliżeniu 1,78 dał stosunek mandatów 1,33. Partia KP zawdzięcza trzeci mandat drobną przewagą 52 setnych nad 48.
A jak by było naprawdę przy metodzie d’Hondta? Jest ona dziwna. Ale jaka jest, taka jest. Przepisy w różnych grach sportowych też wydają się dziwne, ale sportowcy muszą je respektować. Co by powiedział sędzia, gdyby Robert Lewandowski oświadczył, że jemu się nie podoba, że nie można łapać piłki w rękę i złapał?
Jak już wiemy, głosy oddane na poszczególne partie dzielimy przez kolejne liczby i wybieramy siedem największych. U nas obliczenia są łatwe:
Stosunek głosów wyborców 64: 36, czyli w przybliżeniu 1,78 dał stosunek mandatów 5:2, czyli dwa i pół.
To nie wszystko. Czytelnicy pewnie nie pamiętają, że w pierwszych wolnych wyborach było nieco inaczej. Zastosowano metodę Sainte-Laguë. Można powiedzieć, że jest bardziej matematyczna. Frakcje głosów oddawane na partie dzieliło się kolejno przez 1, √2, 2, 3, 4 i tak dalej. Tak właśnie było - do wyborów parlamentarnych wchodziła liczba Pitagorasa, wyrażająca stosunek długości przekątnej kwadratu do jego boku. Zobaczmy, co by to zmieniło: to w przybliżeniu 1,41.
Mamy „z powrotem” rozkład 4–3. To pokazuje, jak to wszystko jest umowne.
Mój kącik jest matematyczny; piszę tu o matematyce, a nie o skądinąd bardzo ważnych problemach z urządzaniem świata, który nas otacza. Nie ma matematyki bez zadań. No to chociaż dwa. Najpierw wstęp. Każdy zgodzi się, że jeżeli stosunek głosów jest 50:50, to mandaty powinny być przydzielone po równo. Oczywiście, jeżeli to możliwe, to znaczy, gdy mamy do podziału parzystą liczbę miejsc. Przyjmijmy, że jest ich 2n. No dobrze, a gdy n = 4 (czyli 8 miejsc do podziału), a stosunek wypadł 51:49? „Logika” podpowiada, że to za mało, żeby dzielić „pięć do trzech”.
A gdy będzie 55:45? A gdy będzie 60:40?
Zadanie 1. Przy jakim stosunku głosów metoda d’Hondta jeszcze daje remis, gdy do podziału jest parzysta liczba mandatów, 2n?
Rozwiązanie. Niech x oznacza, jaka część głosów przypadła partii A. Pozostałe 1 - x głosów zdobyła druga partia. Dzielimy przez kolejne liczby naturalne:
Gdy x jest niewiele większe od, to x jest większe od 1 – x, ale niewiele. Liczby z górnego wiersza są liczby z górnego wiersza są wprawdzie większe od tych z dolnego, ale też niewiele i ustawione w porządku malejącym występują na przemian: góra-dół, góra-dół, góra-dół, … Kiedy nastąpi zmiana tego cyklu, to znaczy kiedy będzie góra-dół, góra-dół, góra-góra?
Gdy partia A zdobywa między 50 a 55 procent głosów, d’Hondt dzieli mandaty po równo: 4–4.
Zadanie 2. Znów przyjmijmy, że jest 8 miejsc. Jaki rozkład procentowy głosów da wszystkie miejsca zwycięskiej partii?
Rozwiązanie. Jak i poprzednio, tworzymy ciąg podziałów. Ostatnia liczba z górnego wiersza ma być większa niż pierwsza. Daje to nierówność
Gdy n=4 (osiem miejsc), ułamek ten jest równy, czyli prawie 89%. Jeżeli partia B osiągnie 11% lub mniej, nie dostanie żadnego z ośmiu miejsc. Sprawdźmy, wykorzystując szkolne wiadomości o ułamkach.
Zgadza się, ten przypadek jest graniczny. Gdyby istotnie zdarzyła się tak idealna równość, to nie wiadomo byłoby, komu przypadnie ósmy mandat. Prawdopodobnie ustawodawca to przewidział i jest na to jakiś przepis, ale już niematematyczny.
Mówi się też, że metoda d’Hondta zachęca partie do tworzenia koalicji. Z matematycznego punktu widzenia na pewno tak. Ale tylko matematycznie. Głosy na koalicję dwu lub więcej partii nie muszą być sumą głosów na poszczególne partie - z różnych względów wyborcy mogą się zniechęcić i uciekać. Na razie to ja uciekam jednak od takich zagadnień. To nie moja działka.
***
Spośród innych pomysłów, jak przeliczać głosy na miejsca w parlamencie, wspomnę dwa sposoby (bardzo podobne zresztą), żeby dzielić te miejsca nie proporcjonalnie do liczby oddanych głosów, tylko proporcjonalnie do… ich kwadratów albo sześcianów. Znalazłem je w angielskiej „Mathematical Gazette”. To jeszcze bardziej rozdmuchuje drobne różnice. Zobaczmy. W metodzie „kwadratów” stosunek 64:36 (czyli 16:9) zmienia się 16²:9², czyli 256:81. Można łatwo obliczyć, że daje to rozkład 5–2. Gdybyśmy stosowali sześciany, byłoby „jeszcze gorzej”: 6–1. To jeszcze bardziej faworyzuje duże partie. Niewielkie różnice w liczbie głosów dają duże różnice wyników. Matematycznie to prosty fakt: funkcja kwadratowa rośnie szybciej niż liniowa, a sześcienna szybciej niż kwadratowa.
Jak widać, trochę się to nam komplikuje. Ale to nie wszystko. Pójdziemy jeszcze wyżej.
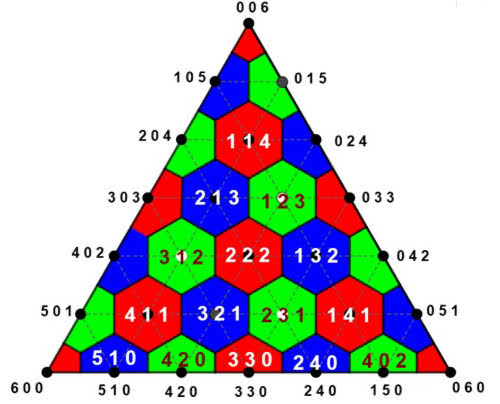
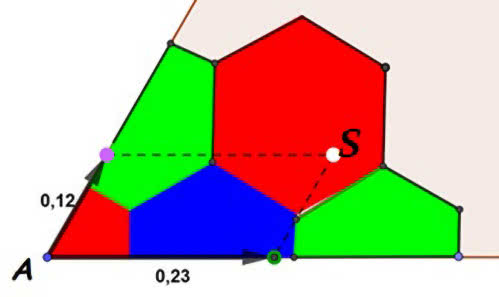
Z mojego, na wskroś matematycznego punktu widzenia następuje teraz zasadnicza część artykułu. Wyraziłem już pogląd, że najbardziej sprawiedliwa jest metoda geometryczno-fizyczna, oparta na pojęciu środka ciężkości. Gdy jednak w wyborach startuje więcej partii niż dwie, musimy sięgnąć do wiedzy z geometrii płaskiej, przestrzennej lub tej w wymiarach większych niż 3. Co samo w sobie byłoby interesujące i dowodzi, że nawet najbardziej abstrakcyjna matematyka ma zastosowanie w konkretnych problemach. Nie wiem tylko, ilu wyborców zrozumiałoby, o co chodzi… Ale zobaczmy. Gdy są trzy partie, możemy uciec się do trójkąta. Przyjmijmy, że jest sześć miejsc (mandatów), a partie dostały odpowiednio 61, 24 i 15 procent głosów.
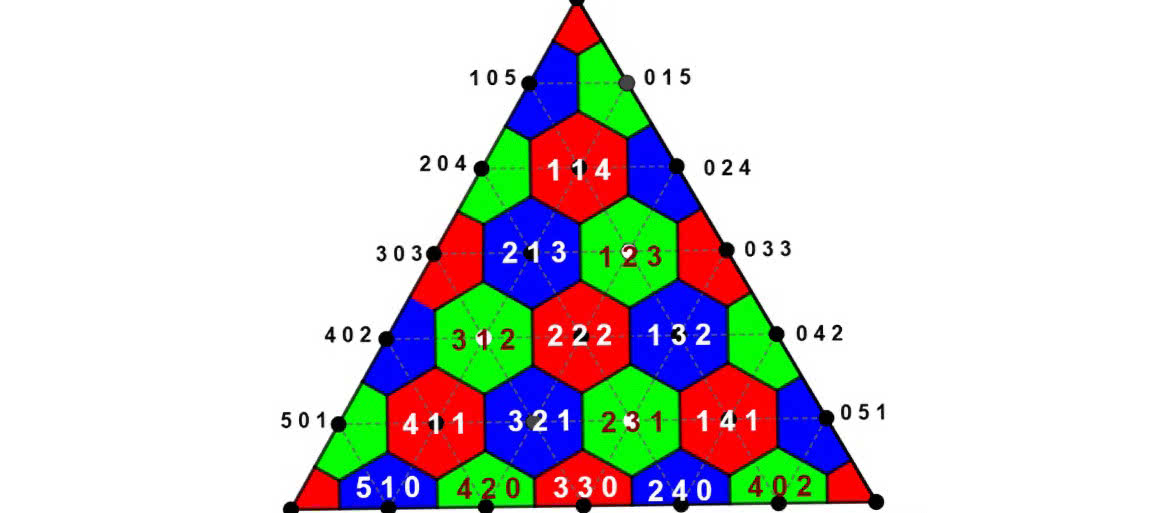
Na blacie stołu rysujemy trójkąt równoboczny i dzielimy go na wielokąty, jak na rysunku 3. W narożnikach trójkąta wiercimy otwory, przeciągamy przez nie cienkie linki, które wiążemy razem. Do tych linek przyczepiamy ciężarki o wagach proporcjonalnych do liczb oddanych głosów na partie. Obszar, w którym ustawi się węzeł, pokazuje rozkład mandatów, jaki powinien przypaść poszczególnym partiom. Na rysunku 4 mamy przykład 65–23–12. Fizyka w zgodzie z geometrią wyrokują: środek ciężkości S jest w sześciokącie, w którym obwiązuje rozkład 4–1–1.
Zadanie 3. A co na to d’Hondt? A Sainte-Laguë?
Oczywiście nie trzeba niszczyć stołu. Każdy się domyśli, że wystarczą jakieś rachunki. Kilkanaście lat temu zrozumiałby je każdy uczeń gimnazjum, no, powiedzmy raczej: ostatniej klasy gimnazjum. Dziś… gimnazjów już nie ma. Nie będę więc tych rachunków przytaczał. Wspomnę tylko, że wagi tych przyczepianych ciężarków mają ładną nazwę: współrzędne barycentryczne.
***
A teraz zadanie z geometrii przestrzennej. Na rysunku 3 zaznaczone obszary to sześciokąty (albo ich fragmenty). Gdy mamy cztery partie, musimy już pracować z czworościanem i ciąć go płaszczyznami. Jakiego kształtu będą części wewnętrzne? I jeszcze zadanie dla studentów wydziałów matematycznych: a w przestrzeni dowolnego wymiaru n?
Odpowiedź: w przestrzeni trójwymiarowej będą to ośmiościany foremne, a w wyższych wymiarach… ich odpowiednik, czyli bryły dualne do kostki wymiaru n.
I tak od prostej matematyki wyborczej doszliśmy do geometrii w przestrzeniach wysokiego wymiaru. Wystarczy tego bujania w obłokach. Przed nami już prawdziwe, niematematyczne wybory.
Michał Szurek