Atomy symetrii

Tytuł tego odcinka Rozmaitości Matematycznych mało komu coś wyjaśnia. Po kolei.

Wszyscy wiedzą, co to jest atom. To coś niepodzielnego - w każdym razie normalnie, spokojnie. Wiemy, co może być, gdy zrobimy to gwałtownie.

Już Demokryt (ok. 460 - ok. 370, oczywiście p.n.e.) doszedł do wniosku, że atomy muszą istnieć. Filozofowie potem dyskutowali, czy wypełniają one całą przestrzeń (jak sześcianiki), czy może tylko jej część (jak kulki). Tak czy owak, my sami składamy się z atomów i od ich położenia zależy, kim jesteśmy.

Przypomnijmy sobie, że chemiczną tablicę Mendelejewa otwiera wodór, H. Atom wodoru jest najprostszym z możliwych. Wokół protonu krąży po orbicie jeden elektron. Nie spada na jądro wskutek trudnych do pojęcia zjawisk kwantowych, których nie tylko autor tego artykułu nie rozumie.

Można powiedzieć, że atomem geometrii jest punkt. Wszystkie figury składają się z punktów i tylko od ich wzajemnego położenia zależy, czy mamy do czynienia z kwadratem, parabolą, kulą czy skomplikowaną, powyginaną powierzchnią.

Pierwiastki chemiczne są różne i mają różne atomy. Czy jest jakieś podobieństwo z matematyką? O tym jest ten artykuł. Jest wiele struktur matematycznych i na ogół występują wśród nich obiekty proste - to takie, których nie da się podzielić na mniejsze. Za każdym razem ma to nieco inny sens, zależny od konkretnej teorii matematycznej, w której się poruszamy.

Najwcześniej (bo w pierwszej połowie XIX wieku) wyodrębnioną taką strukturą algebraiczną jest grupa. Najzwięźlej to tak. Grupa to zbiór, teoretycznie dowolnych obiektów, w którym mamy jakieś działanie. Nie byle jakie, ale podlegające pewnym prostym warunkom, o których nie będę pisał. Często działaniem tym jest dodawanie, często mnożenie, ale równie często grupy pojawiają się jako zbiory pewnych funkcji, operacji, przekształceń, akcji - tam, gdzie „coś się dzieje”. Warunkiem jest, by te procesy były powtarzalne: jeżeli wykonamy coś, to możemy dalej wykonywać inną czynność… z tej samej grupy. Przykłady: dodawanie liczb, tasowanie kart, nakładanie funkcji jedna na drugą, stawianie kroków na płaszczyźnie (matematycznie: przesuwanie o wektor), rzucanie piłką… o, właśnie. Na tym sportowym przykładzie da się dobrze zrozumieć, o co chodzi w pojęciu grupy.

Wrócę z przyjemnością do moich szkolnych czasów i lektury książki Szczepana Jeleńskiego „Lilavati”. Była to obowiązkowa lektura każdego młodego człowieka - a zatem i moją - zainteresowanego matematyką. Tytuł książki pochodzi od imienia księżniczki hinduskiej, biegłej w matematyce. Streszczę jedną z opowieści tam zawartych. Dwanaście dziewcząt bawiło się piłką w nieskomplikowany sposób. Ustawione w koło, rzucały do siebie kolejno, po obwodzie. Łatwo pojąć, że szybko im się to znudziło. Padła propozycja: „Rzucajmy co druga”. Zaprotestowała Hanka, „która w obliczeniach liczbowych była tak prawie biegła, jak sama Lilavati” i wyjaśniła, że w ten sposób tylko połowa będzie się bawić, a druga połowa stać i patrzeć. „No to co trzecia albo co czwarta”. „To jeszcze gorzej, ale możemy rzucać co piąta; wtedy każda dostanie piłkę”.

To, co zrobiła Hanka, to dowód, że grupa Z₁₂ nie jest grupą prostą. Wyjaśniam. Litera Z oznacza liczby całkowite (od niemieckie Zahl = liczba), a 12 odnosi się tutaj do liczby uczestniczek zabawy, tyle że w algebrze numerujemy od 0 do 11. Jednak w symbolu Z₁₂ mieści się również to, że liczby te dodajemy jak godziny na zegarze (matematycy mówią na to modulo 12). Przecież jeżeli przychodzimy do szkoły na ósmą i zostajemy w niej sześć godzin, to wychodzimy o drugiej. Nie ma nic dziwnego w tym, że 8+6=2. Godzina 12 w nocy to godzina zerowa. Tylko w kolejnictwie godzina 24.00 różni się od 0.00. Pociąg przyjeżdżający według rozkładu o północy ma w rozkładzie „przyjazd 24.00”, a odjeżdżający o północy „odjazd 0.00”. Matematycznie nie ma potrzeby mówić o godzinie 12 (w nocy). Jest tylko 0.00.

Ścisłe określenie matematyczne jest takie: Z₁₂ to liczby 0, 1, 2, 3 ,4, 5, 6, 7, 8, 9, 10, 11, które dodajemy modulo 12 - tak jak godziny na zegarze. Hanka wyodrębniła zatem w grupie Z₁₂ podgrupy prostsze. Dziewczęta mogą się podzielić na przykład na trzy zespoły po cztery panienki w każdym. Pierwszy zespół rzuca do siebie czerwoną piłką, drugi zieloną, a trzeci niebieską. Bawią się niezależnie. Grupa rozpada się na „warstwy” - termin używany w algebrze właśnie w tym sensie. Mamy zatem trzy warstwy: czerwoną, zieloną i niebieską. Możemy to ująć algebraicznie: jeżeli będziemy numerować od zera, to w pierwszej warstwie będą liczby podzielne przez 3 (a zatem postaci 3n), w drugiej liczby postaci 3n+1, a w trzeciej 3n+2.

Król Sobieski miał trzy pieski:
Czerwony, zielony, niebieski.

(dziecięca wyliczanka)

Nie dałoby się wyodrębnić mniejszych podgrup, gdyby jedna z dziewcząt odeszła, albo przeciwnie: gdyby przyszła nowa. Jedenaście albo trzynaście dziewcząt może rzucać co druga, co trzecia, czwarta i tak dalej. Każda w końcu dostanie piłkę od koleżanki. Tak będzie dla siedemnastu, dziewiętnastu, dwudziestu trzech uczestniczek tej (teraz to już bardzo nudnej) zabawy. Co to za liczby 11, 13, 17, 19, 23 i tak dalej? Musimy zgadnąć, o co mi chodzi. Tak jest, właśnie o to. To są liczby pierwsze. Co z tego wynika? Odkryliśmy, że ogólniej:

Gdy p jest liczbą pierwszą, to grupa cykliczna Zp jest prosta.

Określenie, że grupa jest „cykliczna” można trak-tować dosłownie: panienki ustawione są w kółeczku i podają sobie piłkę po obwodzie. Jeżeli na naszym zegarku sekundnik przeskakuje co sekundę, to porusza się w grupie cyklicznej Z₆₀. Dni tygodnia biegną od stuleci w rytmie grupy Z₇, a gdyby nie reforma kalendarza według Grzegorza XIII z 1582 roku, moglibyśmy powiedzieć, że od początku chrześcijańskiej rachuby czasu. Gdyby nie było lat przestępnych, to moglibyśmy powiedzieć, że dni upływają nam według grupy cyklicznej Z365.

***

No to mamy zadanie: jakie są inne grupy proste? Co jest tymi „atomami symetrii”, grupami niepodzielnymi na mniejsze?

Już Felix Klein w 1870 roku wiedział, że grupa A₅ jest prosta, a nawet, że wszystkie inne A_n też są proste. Właśnie od n=5. Znów liczba 5 okazała się wyjątkowa.

Dla każdej liczby n≥5, grupy A_n są proste.

Nie wyjaśniłem, co to za grupy. Już mówię. Pokażę na przykładzie n=5. Mamy 5 liczb, powiedzmy 1, 2, 3, 4, 5. Ustawmy je po kolei, tak właśnie: 1, 2, 3, 4, 5. Zrobię jedną zamianę; powiedzmy przestawię piątkę i trójkę. Dostanę kolejność 1, 2, 5, 4, 3. Zrobię następną zamianę, powiedzmy 1 na 2. Mam 2, 1, 5, 4, 3.

Jeden plus jeden to dwa. Po dwóch zamianach z 1, 2, 3, 4, 5 zrobiło się 2, 1, 5, 4, 3. I to jest budulec grupy A₅ i każdej innej A_n . Dokonujemy parzystej liczby zamian. Mogą być dwie, cztery, sześć albo osiem i więcej, ale nie jedna, trzy, pięć, siedem i tak dalej. Wszystko, co otrzymamy, to właśnie grupa A₅ (i ogólniej, A_n). Symbol A na jej oznaczenie pochodzi od jej nazwy: grupa alternująca (można sobie też tłumaczyć, że pochodzi od alternatora, czyli prądnicy prądu zmiennego).

Można zrozumieć, dlaczego parzystość jest ważna. Jedziemy samochodem, a za nami daje sygnał karetka pogotowia. Chcemy usunąć się jej z drogi. Patrzmy w lusterko nad kierownicą i widzimy coś dziwnego. Choć lustro przemienia lewo i prawo, to widzimy prawidłowy napis: AMBULANS. Wiemy dlaczego. Napis na karetce zrobiono w odbiciu lustrzanym SNALUBMA.

Z grupą A₅ spotkamy się także w geometrii i to co najmniej w dwóch miejscach. Jest to po pierwsze grupa złożona ze wszystkich obrotów i ich złożeń bryły, znanej już dobrze w starożytności: dwunastościanu foremnego. A także jest to grupa zbudowana z obrotów bryły czterowymiarowej, której płaskim rysunkiem jest pięciokąt z przekątnymi. Niewprawnym Czytelnikom może to trudno sobie wyobrazić. Spieszę zapewnić, że wprawnym też.

***

Teraz, po szkolnemu: powtórzenie przerobionego materiału. Mamy już dwie nieskończone serie grup prostych - atomów symetrii:

Z₂, Z₃, Z₅, Z₇, Z₁₁, Z₁₃, Z₁₇, Z₁₉, Z2₃, Z₂₉, Z₃₁, Z₃₇, Z₄₃, … - po wszystkich liczbach pierwszych oraz A₅, A₆, A₇, A₈, A₉, A₁₀, A₁₁, A₁₂, …. - po wszystkich liczbach od n=5.

I jeszcze komentarz. Terminu „grupa prosta” używam oczywiście w określonym, matematycznym sensie. Wbrew temu, jak może można to rozumieć, przymiotnik „prosta” nie jest synonimem słowa „nieskomplikowana”. Grupy proste mogą być bardzo, bardzo skomplikowane. Odwrotnie - wiele nieskomplikowanych grup wcale nie jest prostych.

***

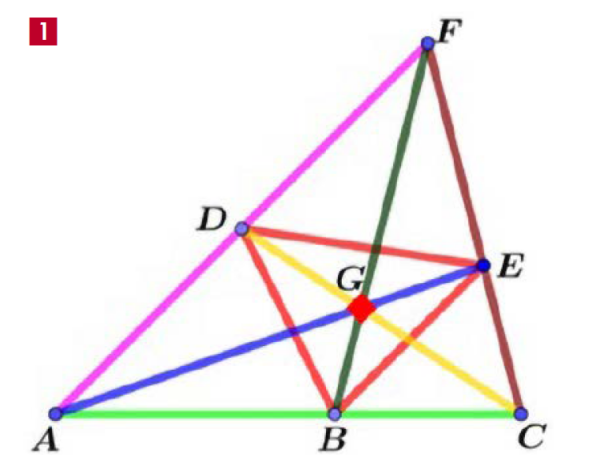
Poprzedni odcinek Rozmaitości Matematycznych był o dwóch liczbach, które lubią wzajemnie swoje towarzystwo: 60 i 168. Na liście grup prostych też zaj-mują miejsca koło siebie. Następną po 60-elementowej grupie A5 jest bowiem grupa prosta o 168 elementach, związana z ciekawą, lecz bardzo elementarną, szkolną konfiguracją siedmiu punktów: trzy wierzchołki trój-kąta, trzy punkty na bokach i punkt w środku, jak na rysunku 1. Napisałem „w środku”, ale powinienem był napisać „wewnątrz”, bo wszystko jedno, jaki jest trójkąt i jakie punkty wybieramy na bokach, byle trzy proste AE, BF i CD miały punkt wspólny.

Tu wkracza geometria rzutowa. Co to jest geometria rzutowa? W przestrzeni rzutowej mamy coś, co nazwiemy punktami i coś, co nazwiemy liniami prostymi. Wszystko jedno, co to jest - punktami mogą być nawet krzesła albo pluszowe misie, byle były spełnione takie warunki:

(P1) Przez dwa różne punkty przechodzi linia prosta i tylko jedna.
(P2) Dwie różne proste przecinają się w jednym punkcie.
(P3) Każda prosta przechodzi przez co najmniej 3 punkty.
(P4) Istnieją co najmniej trzy różne punkty niewspółliniowe.

Jak na siedmiu punktach zbudować geometrię? Można tak. Każda z trójek ABC, ADF, AGE, BGF, CEF, CGD wyznacza prostą. Przyjmujemy właśnie, że innych punktów na tych prostych nie ma. Umówmy się, że punkty B, D, E też leżą na jednej prostej. Mamy siedem punktów, siedem prostych, po trzy punkty na każdej prostej, przez każdy punkt przechodzą trzy proste a każda para punktów należy do jednej prostej. To jest kompletna geometria, warunki (P1)-(P4) są spełnione! A że nieco prymitywna? No cóż, taka już jest. Nazywa się płaszczyzną Fano - od nazwiska włoskiego matematyka Gino Fano (1871–1952).

Zaraz, zaraz. Punkty B, D i E na rysunku 1 przecież nie leżą na jednej prostej, więc jak można się umówić, że leżą? Tu daje znać o sobie siła metody aksjomatycznej. W warunkach (P1) i (P4) nie precyzujemy, czym są „punkty” i „proste”. Gdyby punktami były kolorowe pluszowe misie, moglibyśmy przyjąć warunek, że misie są „współliniowe”, gdy mają uszka tego samego koloru. To znaczy „moglibyśmy” przyjąć, jeżeli spełnione by były warunki (P1)-(P4).

Każda teoria matematyczna, która ma model, jest niesprzeczna. Przełóżmy aksjomaty na nieco zbeletryzowaną opowieść. W pięknej pagórkowatej okolicy, w gminie Podgórnej, leżą miejscowości: Andrzejówka, Bereście, Chełm, Dębowiec, Emilia i Feliksów. Między nimi wznosi się wysoka góra, Giewont. Wójt gminy (matematyk na emeryturze) zaprojektował siedem szlaków turystycznych. Przez każdą z sześciu miejscowości i przez Giewont przechodzą trzy szlaki. Są zatem trzy szlaki łączące dalsze miejscowości: różowy ADF, brązowy FEC i zielony ABC. Z każdej miejscowości można wejść na Giewont (niebieski AGE, ciemnozielony FGB i żółty CGD). Jest jeszcze szlak dolinny dookoła Giewontu, BDE. Wszystko się zgadza. Punkty to miejscowości, linie proste to szlaki.

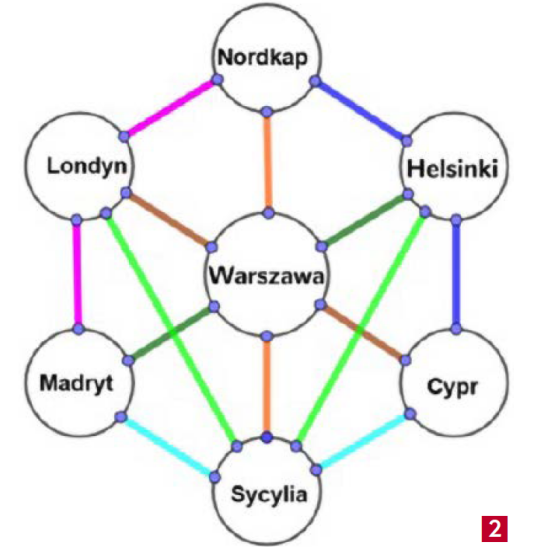
A oto inny opis płaszczyzny Fano. Z pozoru jeszcze bardziej niepoważny, ale z punktu widzenia geometrii rzutowej - całkiem na miejscu. Wyobraźmy sobie, że tanie linie lotnicze Polśmig oferują loty na siedmiu trasach europejskich, jak na rysunku 2.

Te trasy to NLM, NWS, NHC, LSH, HWM, MSC, LWC. To są linie proste płaszczyzny Fano w wersji linii lotniczej Polśmig. Każdy odcinek należy do jednej linii. Każde dwie linie przecinają się w jednym punkcie. Każdy punkt leży na trzech prostych. Każda prosta ma trzy punkty. Nasza teoria ma zupełnie dobry model. Wszystko się zgadza. Modeli płaszczyzny Fano jest oczywiście bardzo wiele.

***

Co to jest kolineacja? Jest to przekształcenie, które nie wykrzywia linii prostych. Co było linią prostą, zostaje nią. Przykłady - pod inną nazwą - znamy ze szkoły. Jeżeli napiszę MŁODY TECHNIK, a potem pochylę tekst (napiszę kursywą): MŁODY TECHNIK, to dokonałem pewnej kolineacji: co było na jednej linii prostej, zostało. Z odcinków nie zrobiły się łuki, z okrągłego O zrobiła się pochylona elipsa. Ile jest kolineacji płaszczyzny Fano? No, właśnie, 168. To nawet nietrudno udowodnić za pomocą prostej algebry liniowej (początek pierwszego semestru przedmiotu „matematyka” na tych studiach, gdzie… ona jest wykładana). I oto dotarłem do głównego celu tego odcinka Rozmaitości Matematycznych, a mianowicie:

Grupa kolineacji płaszczyzny Fano jest kolejną grupą prostą po 60-elementowej A5. Jest kolejnym „atomem symetrii”. Ma 168 elementów i jest przykładem na to, że liczby 60 i 168 lubią być koło siebie.

***

Co dalej? Jakie są inne atomy symetrii, inne grupy proste? To długa opowieść i nie na ten odcinek. Jest jeszcze 18 serii grup pochodzących od tak zwanych algebr Liego - od nazwiska matematyka norweskiego (a nie chińskiego, jak można by przypuszczać) Sophusa Lie (1842–1899) i - co jest bardzo, ale to bardzo dziwne - dwadzieścia sześć grup niemieszczących się w tej klasyfikacji. Dwadzieścia sześć i ani jednej więcej. Są one niewyobrażalnie olbrzymie. Największa z nich, wciąż kryjąca wiele tajemnic, nazywa się nawet Monstrum. Nic dziwnego, bo ma 2⁴⁶∙3²0∙5⁹∙7⁶∙11²∙13²∙17∙19∙23∙29∙31∙41∙47∙59∙71=808 017 424 794 512 875 886 459 904 961 710 757 005 754 368 000 000 000 elementów. Czy możemy sobie wyobrazić atom, który ma tyle elektronów? elektronów? Albo płatek śniegu o tylu ramionach? A tyle elementów ma grupa symetrii, nasze miłe Monstrum, największa grupa prosta. Jest tak samo prosta, jak moja gra w piłkę z wnukiem („łap i rzucaj”, zero jeden, grupa Z₂), jak 13 dziewcząt bawiących się piłką, jak parzyste symetrie najważniejszej bryły platońskiej (dwunastościanu), jak 168-elementowa grupa kolineacji płaszczyzny Fano. Monstrum?Tak, ale matematycy mówią też o niej friendly giant. Taki miły hipopotam.

***

Na zakończenie odcinka zobaczmy, że dziwne geometrie też się przydają. Najpierw o pewnej loterii, a właściwie grze.

Loteria, a właściwie gra, jest nieskomplikowana. Jest 14 liczb, od 1 do 14. Jedna z trójek jest wygrywająca. Wybieramy trzy liczby. Jeżeli trafimy przynajmniej dwie, wygrywamy. Możemy wyobrażać sobie, że są to wyścigi konne i należy trafić dwa konie z pierwszej trójki, niezależnie od porządku.

Czy możemy sobie zagwarantować wygraną w tej grze? Możemy oczywiście obstawić każdą możliwą trójkę, ale to trochę tak jak w totolotku. Jak wygrać w grze z „6 z 49”. Ano, obstawić wszystkie możliwości. Rada przypominająca metodę odróżniania banknotów prawdziwych od fałszywych na podstawie ich popiołu.

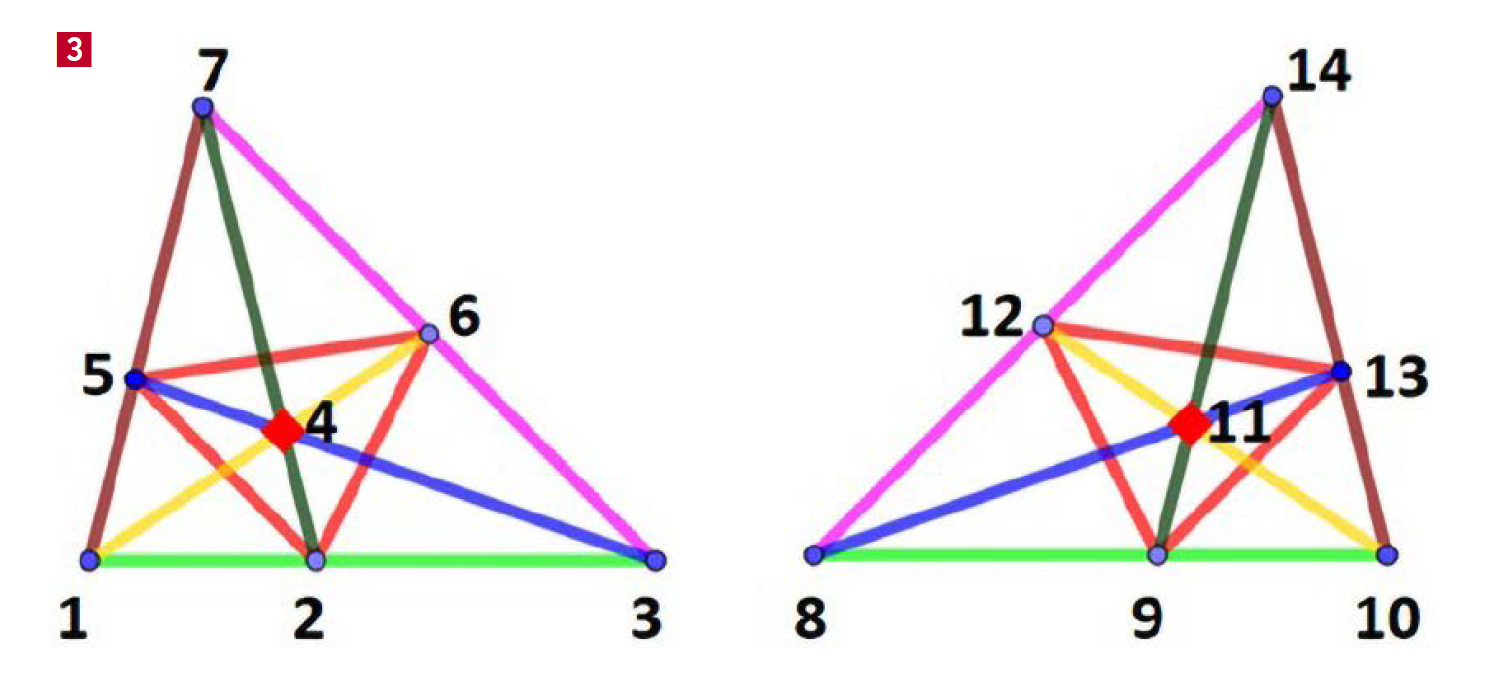
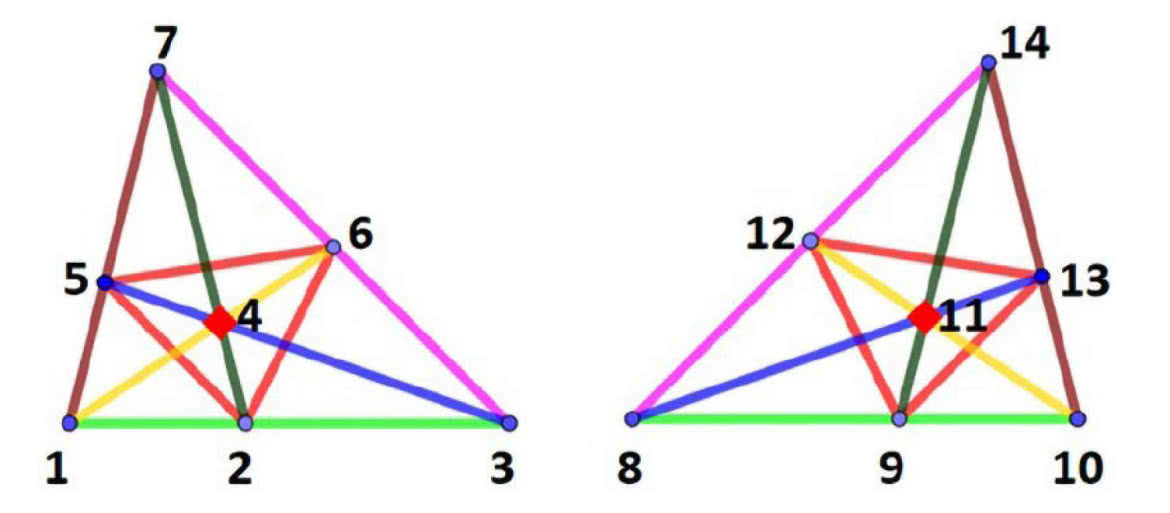
Ale jeżeli skorzystamy z geometrii rzutowej i płaszczyzny Fano, to 14 biletów da stuprocentową wygraną. Oto przepis. Rozpatrujemy dwie płaszczyzny Fano (rysunek 3). Numerujemy ich wierzchołki, pierwszej od 1 do 7, a drugiej od 8 do 14. Obstawiamy 14 trójek, wybierając z pierwszej i drugiej płaszczyzny te, które leżą na jednej prostej: 1 2 3, 1 4 6, 1 5 7, 2 4 7, 2 5 6, 3 4 5, 3 6 7, 8 9 10, 8 11 13, 8 12 14, 9 11 14, 9 12 13, 10 11 12

Niech wygrywającą trójką będzie a, b, c. Co najmniej dwie z tych trzech liczb leżą na jednej z dwóch wybranych płaszczyzn Fano. Niech to będą a i b. Ale przecież obstawiliśmy wszystkie proste z obu płaszczyzn, zatem i prostą przez a, b. Możemy iść do kasy po wypłatę.

W rozszerzonej wersji ta gra znana jest pod nazwą Dobble albo Spot it - wyśledź to. Jest 57 (albo 55, zależnie od wersji) kart, na każdej z nich 8 symboli (zwykle są to gwiazdki, kółka itp.). Karty rozdaje się w zwykły sposób, po kilka (zależnie od wariantu gry). Ktoś wykłada pierwszą kartę. Gracze szukają wśród swoich kart takich, które mają ten san sam symbol co karta (potem: karty) na stole. Kto znajdzie pierwszy, ten kładzie swoją na stole.

Jest to, owszem, ciekawa gra na spostrzegawczość. Związany jest z nią problem matematyczny: jak sprawiedliwie zaprojektować karty? Chodzi o to, żeby każde dwie karty miały ze sobą tylko jeden wspólny symbol.

Napisałem, że jest to „rozszerzony wariant” poprzedniej gry. No, bo tak: przyjmijmy, że kart jest siedem. Umieszczamy na nich po trzy rysunki, wybrane na przykład spośród albatrosa, bociana, czapli, dzięcioła, emu, flaminga i gołębia - tak jak wójt gminy Podgórnej wyznaczył szlaki, a więc adf, fec abc. age, fgb, cgd, bde. Każde dwie proste na płaszczyźnie rzutowej przecinają się w jednym punkcie - każde dwie karty mają tylko jedno wspólne oznaczenie. Problem rozwiązany.

Wracamy do gry Dobble. W geometrii rzutowej mamy takie oto twierdzenie:

Płaszczyzna rzutowa PG(2, n) ma n²+n+1 punktów i tyle samo prostych. Każde dwie proste mają jeden punkt wspólny. Na każdej prostej jest n+1 punktów. Wyjaśniam, o co chodzi. Najpierw podstawmy n=2. Dostaniemy PG(2,2) - a to jest płaszczyzna Fano. Weźmy teraz n=7, czyli skonstruujmy płaszczyznę PG(2,7). Otrzymamy 7²+7+1=57 punktów i 57 prostych, a na każdej po 7+1=8 punktów. Karty zaprojektowane… tylko musimy wiedzieć, czym jest owo PG(2, 7).

***

Artykuł zrobił się przydługi. Na szczęście w XXI wieku mogę Czytelnika zostawić w pewnym zawieszeniu i nie wyjaśnić do końca, jak wygląda płaszczyzna PG(2,7). Jej opis znajdziemy w Internecie, może nam pomóc Apolonia Inteligentna - to jest moje spolszczenie skrótu AI. Znajdziemy też rysunek tej płaszczyzny, podobny do rysunków płaszczyzny Fano, tylko tak skomplikowany, że i tak bym go tu nie skopiował, nie mówiąc o narysowaniu od nowa.

Michał Szurek