Problem Flawiusza - część 2. Jak się ustawić?

Od nowego roku szkolnego weszła w życie drastyczna zmiana kanonu lektur obowiązkowych z języka polskiego. Wypadną między innymi „Syzyfowe prace” Stefana Żeromskiego. Może i słusznie – walka o niepodległość w czasie rozbiorów ponad 100 lat temu to już odległa historia, która nie trafia do pokolenia, urodzonego w bieżącym tysiącleciu. Jest w tej powieści drobny epizod – jak wiejski nauczyciel stara się ukryć jedynego ucznia, który coś umie. Ukryć – żeby jego wywołanie do odpowiedzi w obecności carskiego wizytatora wyglądało na przypadkowe.

Innym matematycznym akcentem w powieści jest zmaganie się Radka z wzorem na objętość ostrosłupa ściętego. Po stosownej podpowiedzi Radek daje sobie świetnie radę. Ze smutkiem stwierdzę, że zadania tego nie rozwiąże dziś 99 procent maturzystów. Ze smutkiem, ale i ze zrozumieniem nowoczesności. Odrzucamy „Syzyfowe prace” – obowiązkową lekturę kilku pokoleń.

Mam jednak nadzieję, że książka Kornela Makuszyńskiego „Szatan z siódmej klasy” jest jeszcze znana młodzieży. Przypomnę, że w tej uroczej powieści uczeń siódmej klasy (= przedmaturalnej w II RP), Adaś Cisowski odkrył kod, którym posługiwał się roztargniony nauczyciel historii do wywoływania kolejnych uczniów do odpowiedzi. Dzięki temu odkryciu każdy uczył się tylko tej lekcji, z której miał być odpytany.  Profesor był dumny, że uczniowie zawsze wszystko
umieją. Uczniowie mieli więcej czasu wolnego…

Metoda profesora była prosta – na n-tej lekcji do tablicy byli wywoływani uczniowie o numerach n, n+10, n+20. Uczniów w klasie było 30, więc wszystko szło bez zgrzytów i regularnie. Aż do dnia, w którym profesorowi skleiły się kartki w notesie. Ale dzięki temu geniusz Adasia Cisowskiego przyczynił się do rozwikłania ponad stuletniej tajemnicy domu brata profesora, Iwo Gąsowskiego. Przypomnieć należy, że ów brat był matematykiem i dniami i nocami rozwiązywał pochodzące z XVII wieku równanie Fermata, czyli xⁿ+yⁿ=zⁿ, dla n > 2. Chodzi o rozwiązanie w liczbach całkowitych. Gdy wykładnik jest równy 2, zadanie jest proste i znane już w starożytności; 3²+4²=5². Oczywiście wysiłki Iwo Gąsowskiego nie dawały rezultatu. W „realu” zagadnienie to rozwiązał dopiero brytyjski matematyk Andrew Wiles w 1993 roku.

Wracając jednak do kodu – jak ustawić ludzi, żeby przy regularnym odliczaniu wybrać pewną grupę. W zeszłym miesiącu pisałem o tak zwanym problemie Flawiusza. Chodzi o bardzo stare zadanie. W obecnym młodzieżowym slangu to już „suchar”. Przypomnę:

Josef ben Matatia, znany bardziej pod zlatynizowanym imieniem Titus Flavius Iosephus, był żydowskim uczonym, ale zanim stał się z tego sławny, w roku 67 n.e. był przywódcą powstania Żydów przeciwko Rzymianom. Pokonany przez cesarza Wespazjana, dostał się do niewoli. Po dwóch latach Wespazjan go uwolnił, nadał łacińskie nazwisko Flavius i obywatelstwo rzymskie, co dawało szereg przywilejów.

Legenda mówi, że po klęsce powstania Ben Matatia (a więc późniejszy Flavius) schronił się do jaskini wraz z pozostałymi jeszcze 40 żołnierzami. Powstańcy postanowili się raczej wzajemnie pozabijać, niż oddać się w niewolę. Flawiusz próbował ich od tego odwieść, ale perswazje nie odnosiły skutku. Zaproponował tylko ścisły porządek w egzekucjach. Ustawił wszystkich, wraz z sobą, w krąg i liczył: „raz, dwa, trzy”. Każdy, na kogo wypadła trójka, był zabijany. Sam jednak siebie ustawił tak, by być ostatnim w tym makabrycznym procederze. Podobno zresztą kilku ostatnich żołnierzy też postanowiło się poddać.

Gdy znajdujemy się w bezpośrednim stresie (jak Flawiusz), zadania być może… nie zdążymy rozwiązać. Ale nie jest ono specjalnie trudne, jeżeli rozwiązujemy je w spokoju. Wystarczy „policzyć do tyłu” albo zacząć od dowolnego miejsca, wyliczyć, kto będzie ostatni i dokonać stosownego przesunięcia. Wiąże się z tym tak zwana matematyka modularna. Dobrze ją znamy, w każdym razie tę modulo 12 i modulo 30 albo 31. Najłatwiej na zegarze. Jeżeli od 8.00 upłynie sześć godzin, to która będzie godzina? Oczywiście druga. Nieważne, czy mowa jest o godzinach przed- i popołudniowych, czy wieczornych (i wtedy 2.00 to druga w nocy). Możemy powiedzieć, że zegarowo 8+6=2, a na przykład 9+6=3 oraz 11+9=8 i tak dalej. Podobnie – tylko z liczbami 31 albo 30, albo 28, a co cztery lata 29 – będzie z dniami miesiąca. Dwanaście dni po  24 marca wypadnie „24+12=36 marca”, czyli 36–31=5 kwietnia. To jest właśnie arytmetyka modularna.

Jeszcze jedno zadania z takiej arytmetyki. Mam brać pewien antybiotyk co 7 godzin, łącznie 20 tabletek. Zacząłem we wtorek o jedenastej rano. Kiedy przyjmę ostatnią tabletkę? Odpowiedź: (11+20∙7) mod 24=151 mod 24=7. Będzie to godzina 7 rano. Jaki to będzie dzień? Ponieważ 151=6∙24+7, będzie to 6 dni po wtorku, czyli (tu znowu trzeba wziąć modulo 7) – w poniedziałek.

Załóżmy, że z jakichś powodów zależy nam, żeby przy takiej regularności ostatnią tabletkę zażyć o siódmej rano. O której godzinie zacząć ją przyjmować? Odpowiedź: o siódmej.

***

W dawno minionej młodości czytywałem jedną z bardzo niewielu dostępnych wtedy książek popularnych o matematyce: Lilavati Szczepana Jeleńskiego. Tytuł to imię księżniczki hinduskiej, bardzo biegłej w matematyce. „Czytywałem” to dobre określenie – bowiem przeczytałem tę książkę niezliczoną liczbę razy. Dzisiaj wracam do niej, odkrywając w zadaniach z fabułą drugie albo i trzecie dno – co jest zresztą fascynujące. Wydana po raz pierwszy w roku 1930, miała wiele wznowień. Z wydań po 1945 roku zniknęły zadania, których treść nie podobała się ówczesnym władzom. Zresztą, niektóre zadania też nie wytrzymują dzisiejszych kryteriów poprawności politycznej.

Jedno z tych opuszczonych zadań jest następujące:

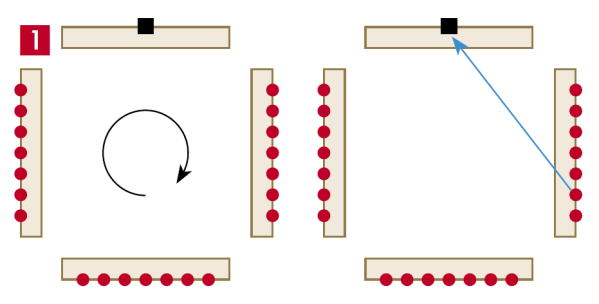
W karczmie stały cztery stoły, dookoła ścian. Weszło 21 zgłodniałych żołnierzy, wracających z manewrów. Zamówili obiad, prosząc jednocześnie gospodarza, by zechciał z nimi spożyć. Rozmieścili się tak, że przy trzech stołach zasiedli żołnierze, po 7 przy każdym, a przy czwartym siadł gospodarz (rysunek 1).

Żołnierze wśród żartów umówili się z gospodarzem, że płacić za wszystkich będzie ten, kto przy liczeniu zostanie ostatni. A liczyć mieli dookoła (biorąc w rachubę i gospodarza) w kierunku obrotu wskazówek zegara, przy czym siódmy miał być zwolniony; zwolniony opuszczał karczmę. Ostatni został ku swojemu zdumieniu… sam gospodarz. Od kogo zaczęto liczyć?

Rozwiązanie jest proste, należy zacząć od żołnierza pokazanego na rysunku 1. Jest to zrozumiałe. Na pewno widzimy, że matematycznie jest to takie samo zadanie, jak problem Flawiusza i mój antybiotyk.

Znacznie trudniejsze od problemu Flawiusza jest zadanie, którego treść budzi teraz w nas jak najbardziej słuszne potępienie. Jak wspomniałem, z przedwojennego wydania Lilavati zostało usuniętych kilka zadań, między innymi to. Cytuję (zachowując ortografię):

Po pełnym morzu na niewielkim statku płynęło 15 chrześcijan i 15 Turków. Nagle zerwała się straszna burza i poczęła miotać statkiem. Kapitan, stwierdziwszy szereg uszkodzeń, oświadczył, że statek skazany jest na zagładę, gdyż nie wytrzyma ciężaru 30 ludzi. Albo wszyscy zginą, albo należy 15 wrzucić do morza, by pozostałych 15 mogło się uratować. Zdecydowano, by rozstrzygnął los, kto ma zginąć, a kto ma na statku pozostać. Postanowiono mianowicie, by ze wszystkich obecnych uformować szereg i licząc kolejno od 1 do 9, każdego dziewiątego wrzucać do morza, póki nie zostanie 15 ludzi. Ten, który rozstawiał zebranych, był chrześcijaninem, uczynił więc to tak, że zginęli kolejno wszyscy Turcy, a zostali sami chrześcijanie.

Taka treść jest dziś oczywiście nie do przyjęcia, ale tuż po drugiej wojnie światowej miała jeszcze inny mroczny podtekst, dla mnie zrozumiały, o którym nawet nie wspomnę. Zmienię za to fabułę na przyjemniejszą. Będzie to bardziej wyrafinowana forma metody profesora Gąsowskiego z powieści Kornela Makuszyńskiego. Pewien profesor matematyki miał taką oto metodę odpytywania uczniów. Brał po kolei do tablicy połowę 30-osobowej klasy w ten sposób, że liczył w myśli kolejno do 9 i odpytywał każdego dziewiątego – aż przepytał 15 uczniów. Metodę tę odkryła pewna bystra uczennica. Przez analogię do Adasia Cisowskiego nazwijmy ją Basią Dębowską. Przed lekcją, która miała być w całości poświęcona odpowiedziom ustnym, Basia wybrała piętnastu, którzy obiecali się nauczyć. Przed lekcją poleciła im usiąść na wybranych miejscach. Profesor był roztargniony – jak przecież każdy matematyk – i niczego nie zauważył. Przepytał piętnastu, każdemu postawił szóstkę i znów wyszedł z klasy dumny ze swoich osiągnięć pedagogicznych.

Jak Basia na to wpadła, trudno zgadnąć. Ale nawet, gdy znamy zasadę, nad samym ustawieniem (czy raczej usadzeniem) uczniów trzeba się trochę napracować. Mają oni być w następującej kolejności. Krzyżyk oznacza tych, którzy się nie nauczyli, kółeczka – tych pracowitych. 

x x x x o o o o o x x o x x x o x o o x x o o o x o o x x o

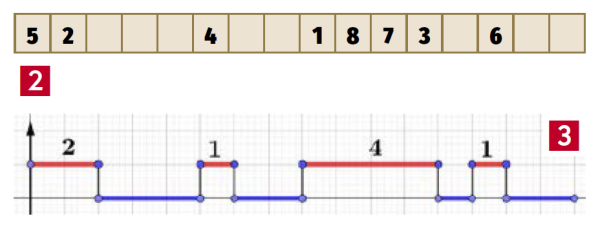
Rysunek 2 pokazuje, co trzeba, z tym, że dla uproszczenia, zamiast n=30, mamy tu n=16, z tą samą zasadą: liczymy do 9. Kolejne liczby wskazują właśnie co dziewiąte miejsce.

Dane z rysunku 2 można zilustrować inaczej. Wykres z rysunku 3 należy tak czytać: najpierw ustawiamy dwóch pilnych uczniów, potem trzech leniwych, jednego pilnego, dwóch leniwych, czterech pilnych itd.

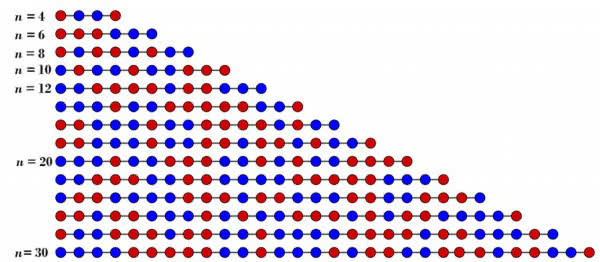
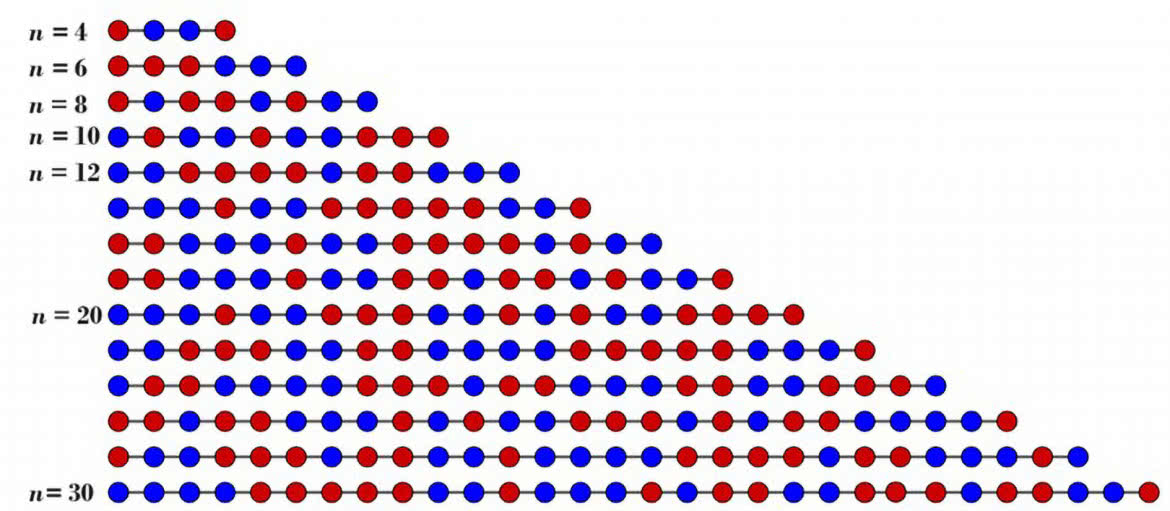
Matematyka zaczyna się tam, gdzie poszukujemy prawidłowości i wzoru ogólnego. Oto kolejny diagram (rysunek 4). Rozstawienie pilnych–leniwych, gdy w klasie jest n uczniów. Liczymy do k=9. Kropki czerwone to ci, którzy umieją, niebieskie – ci drudzy.

Wygląda to ładnie, kolorowo i pstrokato. Jak to jednak ująć matematycznie? Jak znaleźć wzór, z którego to od razu wyniknie? I tu nieoczekiwanie matematyka się poddaje. Nie znamy ogólnej, zgrabnej formuły, którą można zastosować. Z informatycznego punktu widzenia jest łatwiej. Napisanie programu, który to wszystko oblicza, nie jest bardzo łatwe, ale też i niespecjalnie trudne. Jako człowiek, który swój pierwszy komputer osobisty zobaczył, mając ponad 40 lat, nie mam wprawy w pisaniu programów. Sądzę jednak, że dałbym sobie radę z programem, który ma:

Dla danej liczby n i dla danej liczby k wyznaczyć, na których miejscach należy tak posadzić pilnych uczniów klasy mającej tych uczniów 2n, żeby przy odpytywaniu co k-tego pierwszych n uczniów należało do zbioru „pilnych”.

Powiedzmy sobie szczerze: to dobrze, że nie wszystko da się opisać wzorem matematycznym. Ale wróćmy do oryginalnego sformułowania zadania, z wyrzucaniem ludzi za burtę. Aby zapamiętać rozkład, szesnastowieczny matematyk francuski Claude Gaspard Bachet de Méziriac proponuje wyuczenie się dwuwiersza francuskiego

Mort tu ne falliras pas
En me livrant le trepas
albo angielskiego
From numbers aid and art.
Never will fame depart.

Jak pisze Szczepan Jeleński, po polsku można by zastosować taki dwuwiersz:

W morzu szmer – skargi fal,
A serce wita echem żal. 

O co tu chodzi? Ustawmy nasze samogłoski w kolejności alfabetycznej: a=1, e=2, i=3, o=4, u=5. Pokazują one ustawienie. Zanalizujmy każdy z tych dwuwierszy. Samogłoski są tam po kolei o, u, e, e, a, i, a, e, e, i, a, e, e, a. Liczbowo daje to 4, 5, 2, 2, 1, 3, 1, 2, 2, 3, 1, 2, 2, 3, 1, 2, 2, 1. Ustawiamy najpierw czterech „chrześcijan”, potem pięciu „Turków” i tak dalej. W mojej interpretacji Turcy to „zdolni uczniowie”, a chrześcijanie to ci „leniwi”.

***

Wróciłem do tego zadania po – naprawdę – 60 latach. Jak to miło, że matematyka rozwija, nie starzejąc się.  

Michał Szurek