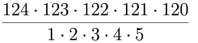Twierdzenie Halla o małżeństwach

Matematycy lubią nadawać twierdzeniom żartobliwe formy. Mamy na przykład „twierdzenie o kanapkach”: każdą kanapkę z masłem i szynką można przekroić jednym cięciem tak, by przepołowić bułkę, masło i szynkę. W analizie matematycznej jest „twierdzenie o dwóch policjantach”: jeżeli idziesz trzymany z dwóch stron przez dwóch policjantów, to trafisz do komisariatu. Chodzi tu o prosty fakt, znany każdemu, kto uczył się podstaw analizy matematycznej: mamy trzy ciągi a,b,c takie, że a≤b≤c. Jeżeli dwa skrajne dążą do tej samej granicy g, to trzeci też ma granicę g. W analizie funkcjonalnej (polskiej specjalności matematycznej lat międzywojennych) mówi się też o twierdzeniu o ziemniakach: skończony zbiór ziemniaków można zapakować do jednego worka – ale tłumaczenie, o co „naprawdę” chodzi, wykracza poza ramy tego kącika.

Trzeba szczerze powiedzieć, że takie żartobliwe podejście spotyka się często z niezrozumieniem i niekiedy wręcz niechęcią do matematyki. „Dlaczego moje pieniądze, prostego podatnika, mają iść na takie bzdury”? Jedyną odpowiedzią jest chyba odwołanie się do poczucia humoru ludzi – oraz przekonanie ich, że to właśnie nie tylko żart, że to jednak czemuś służy, choćby refleksji intelektualnej. A co jest poważne, a co nie, jest bardzo często umowne. Skończyła się olimpiada. Czy rzucanie kijem albo kopanie skórzanej (no, od wielu lat już nie skórzanej) piłki jest czymś poważnym? Po tym przydługim wstępie przejdę do… spraw męsko-damskich w majestacie matematyki. Otóż na Marsa leci wieloosobowa załoga. Podróż jest długa, trzeba wytrzymać. W załodze są kobiety i mężczyźni – tych jest trochę więcej. Po pewnym czasie zaczynają się tworzyć pary. W regulaminie nie jest to zakazane. To przecież pozwala lepiej znieść kosmiczną nudę i frustrację. 

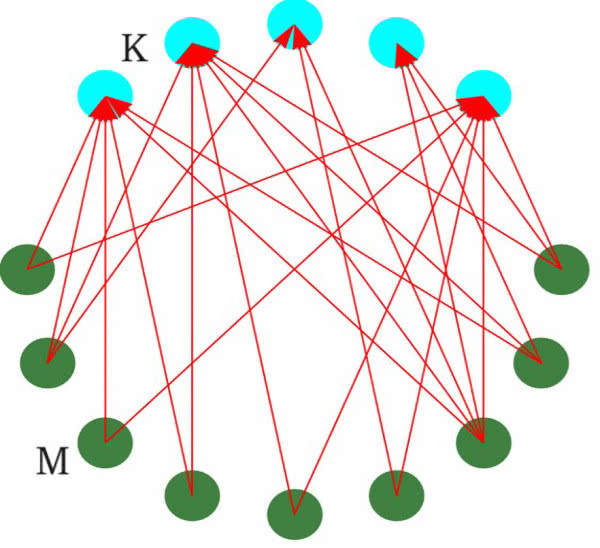
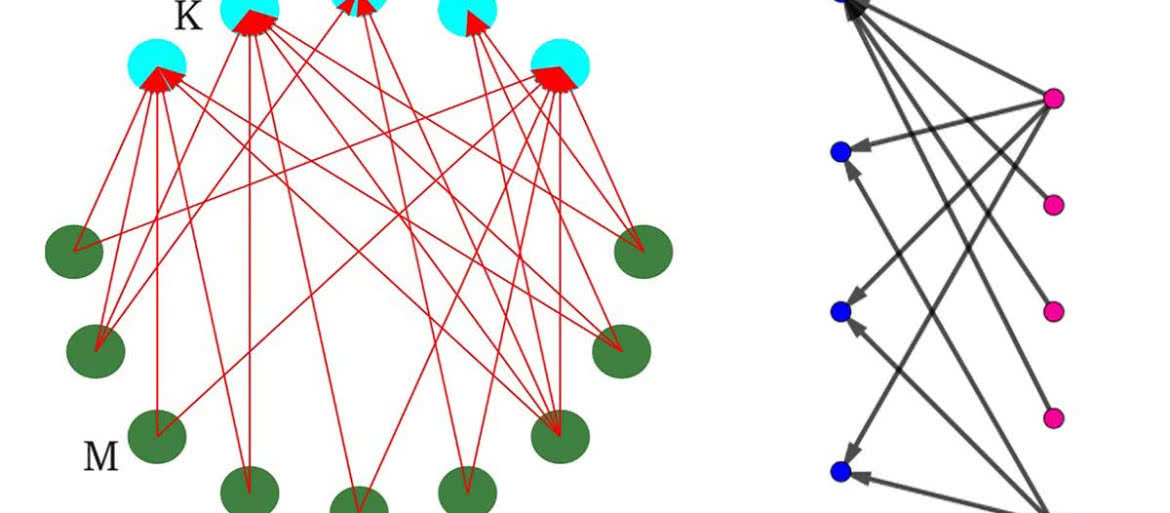
W załodze, jak to w każdej grupie ludzi, jedni lubią się bardziej, inni mniej. I oto wykres (1). Mamy dwie grupy, K i  M –  domyślności Czytelników pozostawiam, skąd taki wybór oznaczeń. Każda osoba z grona K rozważa, z kim ewentualnie mogłaby się związać. Pokazują to strzałki. W wersji „małżeńskiej”: za tego faceta ewentualnie mogłabym się wydać. Inni niech spadają! Co prawda w stanie nieważkości (lecimy przecież na Marsa) to jest niewykonalne.

1.

I teraz wreszcie zagadnienie matematyczne: czy takie przyporządkowanie jest możliwe? Czy każda osoba z grona K znajdzie takiego M, który jest akceptowalny? Oczywiście nie jest to symetryczna sytuacja: jeżeli M>K, to nie każdy M znajdzie swoją K. Cóż, życie (2).

2.
Fot: AdobeStock

O to właśnie chodzi w twierdzeniu, udowodnionym w 1935 roku przez Philipa Halla: takie przyporządkowanie jest możliwe, jeżeli tylko spełniony jest dość oczywisty warunek (zwany teraz warunkiem Halla). Choć oczywisty, jest trochę skomplikowany. Łatwiej go sformułować właśnie w terminach matrymonialnych. Zamiast długiego „tego mężczyznę mogłabym poślubić”, będę pisał „znam go”.

Po  pierwsze: każda kobieta zna co  najmniej jednego mężczyznę.
Po drugie: każde dwie kobiety znają co najmniej dwóch mężczyzn.
Po trzecie: każde trzy kobiety znają (łącznie) co najmniej trzech mężczyzn.
Po  czwarte: każde cztery kobiety znają (łącznie) co najmniej czterech mężczyzn.
Po piąte… i tak dalej.

Jest dość jasne, że jeżeli którykolwiek z tych warunków nie jest spełniony, to nie każda pani znajdzie pana, który jej choć trochę odpowiada. Twierdzenie, o którym opowiadam, mówi, że jest także przeciwnie: jeżeli warunek Halla jest spełniony, to odpowiednie przyporządkowanie istnieje. W locie na Marsa każda astronautka znajdzie swojego astronautę. Gdyby liczba K była równa liczbie M (czyli parytet byłby 50–50), mogłoby być i odwrotnie.

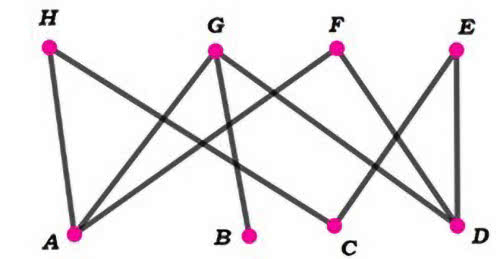
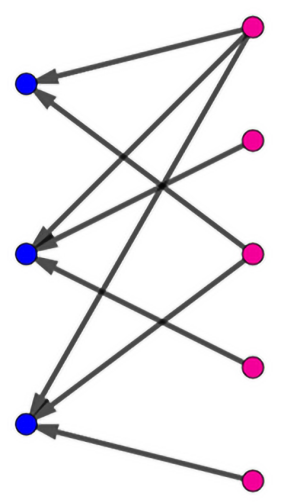
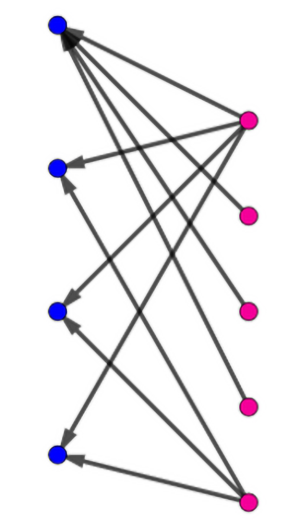
Spójrzmy na następne rysunki. Układ na rysunku 3 nazywa się w matematyce grafem dwudzielnym: są w nim dwa odrębne zbiory, a połączenia są tylko między jednym a drugim – nie ma natomiast połączeń w obrębie jednego zbioru. Na rysunku 4 warunek Halla jest spełniony, na rysunku 5 nie: trzy pierwsze niebieskie kropki są połączone tylko z dwiema czerwonymi.

3.

4.

5.

Dowód twierdzenia Hall jest ciekawy, ale może tylko dla matematyków. Natomiast ważniejsze jest co innego, co  zilustruję dygresją. Jest dość oczywiste, że w Warszawie (Krakowie, Poznaniu, Gdańsku itd.) znajdą się osoby, które mają tyle samo włosów na głowie (i nie jest to liczba zero, bo łysych panów znajdzie się wielu). To bardzo prosto zrozumieć: w każdym z tych miast jest więcej niż powiedzmy, pół miliona ludzi. Mamy mniej włosów na głowie, zatem muszą być osoby równe pod względem liczby włosów. To typowy dowód matematyczny: wykazaliśmy, że takie osoby są. Informatyk powie, że ta informacja nic mu nie daje. Potrzebny jest algorytm, który takie osoby znajdzie.

Podobnie jest z  twierdzeniem Halla. Wiemy już, że taki matching istnieje. Jak go znaleźć? Algorytm nie jest trudny –w odróżnieniu od hipotetycznego pro-gramu na szukanie osób tak samo owłosionych. Nie podam szczegółów, ale idea jest taka: zaczynamy przyporządkowywać, kolejne K do kolejnych M. Jeżeli w  którymś momencie się zatnie, cofamy się o krok i zmieniamy. Jeżeli wyczerpiemy wszystkie możliwości i nie posuniemy się naprzód, cofamy się o następny krok i szukamy, szukamy. Twierdzenie Halla gwarantuje, że za którymś razem musi się udać. Jest to algorytm powolny, ale jak najbardziej wykonalny.

Od mniej więcej dwóch lat panoszy się sztuczna inteligencja. Ja nazywam ją sobie Apolonią Inteligentną. Niektórzy wnioskują, że zabije ona naszą cywilizację, a potem nas wszystkich. Zobaczymy, ale podobnie było z wieloma wynalazkami. A ja poprosiłem Apolonię o napisanie programu na szukanie przyporządkowania w twierdzeniu Halla. Uff, najtrudniej było „jej” wytłumaczyć, jaki graf ma wziąć. Trwało to długo. Nie jestem zręcznym programistą, średnio zaawansowany ktoś napisałby szybciej.

***

Jak wspomniałem na  wstępie, wątpię, żeby to wszystko przydało się w biurze matrymonialnym. Siła twierdzenie Halla – jak większości zagadnień ma-tematycznych – tkwi w przykładach i zastosowaniach. Jest taka maksyma, że lot w abstrakcję musi zaczynać się i kończyć na Ziemi. Astronauci powinni też powró-cić z Marsa, choć podobno zgłaszają się już ochotnicy do lotu w jedną stronę. Ostatecznie w dawnych czasach wielu ludzi emigrowało do Ameryki ze świadomością, że zostaną tam już na zawsze.

Wróćmy do diagramu z rysunku 1. Odczytamy go inaczej. W pewnej dużej firmie są prace do wykonania: K1, K2, K3, … Zbiór prac oznaczymy przez K. Zbiór pracowników niech nazywa się M. Nie każdy pracownik potrafi wykonać każdą pracę, ale do każdej nadaje się kilka osób. Jeżeli spełniony jest warunek Halla, to da się do każdej pracy przydzielić fachowca. Więcej: algorytm (który omówiłem w zarysie) powie, kogo przydzielić do jakiej pracy. Jeżeli firma jest naprawdę duża, to być może ręcznie nie da się tego zrobić. Podobnie jest z układaniem planu lekcji w dużej szkole: do każdego przedmiotu jest kilkoro nauczycieli. Za tak zwanych „moich czasów” oddelegowana do tej pracy wprawna nauczycielka poświęcała na to kilka dni, zużywając kilka ołówków i gumek.

Inne zastosowanie twierdzenie Halla jest może mniej przydatne, chociaż matematyka w sporcie to oddzielny temat i nie chodzi tylko o liczenie punktów. Często po meczach siatkarskich, hokejowych itp. wybierany jest najlepszy zawodnik na danej pozycji. Jak zauważyłem, jest to trochę sztuczne; chodzi o dodatkowe emocje i może nagrody. Oto więc.

Zadanie. W lidze siatkarskiej bierze udział 2n zespołów. Rozgrywki są systemem „każdy z każdym”, po jednym meczu (bez rewanżu). Nie ma remisów. Po każdej kolejce jednemu zespołowi, który wygrał swój mecz w tej kolejce, wręczony zostaje pamiątkowy medal. Wykaż, że można tak to zrobić, żeby w każdej kolejce medal dostał inny zespół.

Rozwiązanie zrozumiemy na przykładzie n =3 (sześć zespołów), niech to będą zespoły a, b, c, d, e, f. Mamy pięć kolejek, niech K={1,2,3,4,5}, M={a,b,c,d,e,f}. Utwórzmy graf: do każdego dochodzą trzy strzałki do trzech elementów zbioru M. Po chwili zastanowienia się dochodzimy do wniosku, że warunek Halla jest spełniony, bo:
W każdej kolejce jest zwycięzca (a nawet trzech).
W każdych dwóch kolejkach jest dwóch zwycięzców (a nawet trzech).
W każdych trzech kolejkach jest na pewno trzech zwycięzców.
W każdych czterech kolejkach jest na pewno co najmniej czterech zwycięzców. Meczów jest 12. Przypuśćmy, że jest tylko trzech zwycięzców. Muszą wygrywać wszystkie mecze, bo 3∙4=12. Ale w którejś kolejce muszą grać ze sobą, nie mogą więc wygrywać wszystkiego.

W pięciu kolejkach jest na pewno co najmniej pięciu zwycięzców, bo nie może być dwóch drużyn, które przegrały wszystkie mecze, a zatem pomysł wręczania medalu za każdym razem innemu zespołowi jest wykonalny. Diagram na rysunku 6 pokazuje rozgrywki z udziałem klubów z Łodzi, Sierpca, Łap, Żywca, Pruszkowa i Szczecina. Nazwy oczywiście są wymyślone przeze mnie. Kropki oznaczają zwycięzców, a czerwone kropki te zespoły, które zostały wybrane jako „drużyny kolejki”. Zauważmy, że choć Ołówek Pruszków wygrał wszystkie mecze, ani razu nie został wyróżniony. Oczywiście tu nie stosowałem algorytmu, tylko wybrałem „na oko”, a co by zrobił algorytm, nie sprawdziłem.

6.

Oto inne zastosowanie. Stworzę smutną fabułę. Pewien obszar leśny podzielono na 100 działek budowlanych. Wycięto drzewa, drewno sprzedano do Finlandii, zabetonowano podjazdy. Każda działka ma tyle samo metrów kwadratowych. Działki sprzedano patodeveloperowi, a niezależnie od tego strażacy – przestrzegając stosownych przepisów – podzielili na mapie teren na 100 obszarów o tej samej powierzchni, ale zupełnie inaczej. Wykaż, że można wykonać 100 przyłączeń wody, żeby na każdej działce budowlanej i na każdej strażackiej znalazło się przyłącze.

Rozwiązanie. Niech K to będą działki budowlane, M – strażackie. Rysujemy graf od K do M i od M do K, łącząc te działki, które chociaż częściowo się pokrywają. Warunek Halla jest spełniony, można kopać.

Twierdzenia Halla ma efektowne zastosowanie w… pewnej sztuczce karcianej. Jest oto dwóch magików. Jeden z nich podaje komuś z publiczności talię 124 różnych kart i prosi o wybranie pięciu. Następnie pokazuje (publicznie) drugiemu kolejno tylko cztery. Ten zgaduje piątą!

Wydaje się to niemożliwe – kart jest za dużo, żeby odtworzyć jedną z brakujących. Ale od czego matematyka? Zauważmy po pierwsze, że pierwszy sztukmistrz decyduje, którą kartę schować. Ile jest możliwych wyborów pięciu kart ze 124? Czytelnicy, którzy pamiętają coś ze szkoły, wiedzą, że jest to 

Nie musimy tego obliczać. Zauważmy tylko, że mianownik jest równy 120 i zostaje iloczyn 124∙123∙122∙121. Teraz obliczmy, ile jest ciągów czterech kart? Pierwszą kartę ciągniemy na 124 sposoby, drugą na 123, trzecią na 122, czwartą na 121. Mamy więc tyle samo możliwości: 124∙123∙122∙121. Jest zatem szansa, aby każdy zbiór zakodować innym ciągiem.

Niech zbiorami będą M (mężczyźni w twierdzniu Halla), ciągami K (kobiety). Warunek Halla jest spełniony, więc można ich pożenić. Innymi słowy, można każdy zbiór pięciu kart jednoznacznie zakodować ciągiem czterech z nich. Osobną sprawą jest algorytm, jak to zrobić, pewien efektowny, autorstwa M. Klebera, znalazłem w czasopiśmie „Mathematical Intelligencer”, tom 24, numer 1 (rok 2002). Zachęcam do zajrzenia tam, a na koniec jeszcze jedno zadanie.

Rozkładamy 52 karty w prostokącie o 13 rzędach poziomych i 4 pionowych (kolumnach). Wykaż, że da się wybrać po jednej karcie z każdej kolumny tak, by nie powtarzały się wielkości (to znaczy, by mieć jednego asa, jedną dwójkę, jedną trójkę i tak dalej).

Jak to zrobić? Zastosować twierdzenie Halla. Jak? Mniej więcej tak, jak przy wyborze najlepszej drużyny siatkarskiej i przyłączy wody do działek.

Twierdzenie Halla znajduje zastosowanie i w matematyce z najwyższej półki. Ma też wiele uogólnień, związanych z trudniejszymi zagadnieniami praktycznymi, na przykład uwzględniających stopień preferencji poszczególnych wyborów, na przykład małżeńskich, ale i stopień kwalifikacji pracowników do poszczególnych zadań (jak w przykładzie z firmą), ale to już inna historia. Zastosowanie „matrymonialne” to tylko przykrywka, trochę z obliczeniem na efekt „wow”. 

Michał Szurek