Liczby, co się lubią

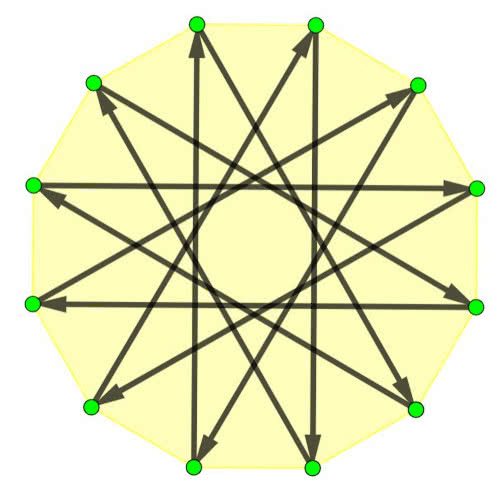
„Osobiście” zetknąłem się po raz pierwszy ze związkiem tych liczb przy lekturze książki Szczepana Jeleńskiego „Śladami Pitagorasa”, mniej więcej 65 lat temu (!). W jednym z zadań 12 dziewcząt, ustawionych w koło, rzucało do siebie piłką. Postanowiły urozmaicić grę, rzucając np. co druga albo co trzecia. Oczywiście pierwszy z tych sposobów wykluczał sześć, a  drugi osiem uczestniczek. Dopiero rzucanie „co piąta” zapewniło, że do każdej piłka w końcu trafi. Można to zilustrować ładnym rysunkiem (1). Matematycznie nie ma w tym nic dziwnego: liczby 5 i 12 nie mają wspólnego dzielnika (mówimy, że są względnie pierwsze).

1.

Wspomniałem Pitagorasa, znanego wszystkim mędrca z VI wieku p.n.e. Również dzięki niemu 5 i 12 się lubią. Występują obok siebie w trójce pitagorejskiej – trójce liczb tworzącej trójkąt prostokątny. Najprostszą taką trójką jest 3, 4, 5. Następna to właśnie 5, 12 i 13. Dziwne (???), że nie ma w Warszawie także linii tramwajowej 13. Może dyspozytorzy nie lubią geometrii?

2.

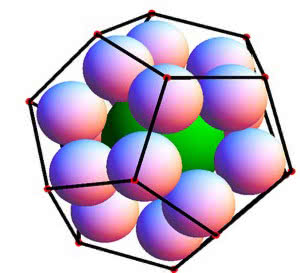
Najbardziej intrygujące jest współżycie naszych dwóch liczb w wielościanie foremnym, będącym dla starożytnych symbolem wszechświata, całości kosmosu i harmonii przedustawnej. To dwunastościan foremny, złożony z pięciokątnych ścian. W każdym wierzchołku schodzą się trzy. 

3.

4.

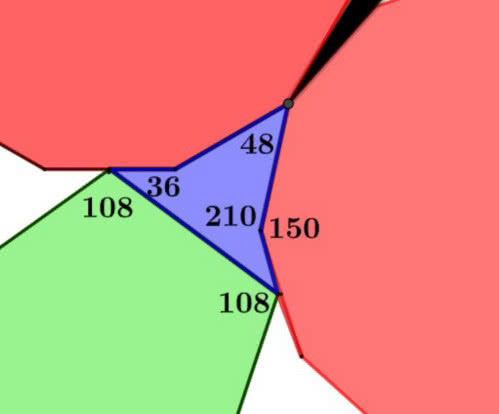
Jest w matematyce zasada dualności. Skoro jest bryła złożona z dwunastu pięciokątów, to może jest i taka, która ma pięć ścian i jest ograniczona dwunastokątami? Niestety, nie ma takich brył. Można jednak ustawić dwunastokąty w pięciokątny ornament (4). To daje łatwe zadanie: wyznaczyć kąty powstałej figury (5) i znacznie trudniejsze: obliczyć wszystkie rozmiary liniowe.

5.

Nasze liczby sąsiadują też w ciągu a_n=2ⁿ–n. Istotnie, mamy w nim po kolei: 1, 1, 2, 5, 12, 27, 58, … Obydwie są kolejnymi liczbami pięciokątnymi, co objaśnia rysunek 6.

6.

Przejdę dalej, do bardziej współczesnej matematyki, rożnej od tej, którą poznawałem, czytając po raz pierwszy „Śladami Pitagorasa”. Czytelnik może się zdziwić: jak to „inna matematyka”? Czyżby zanosiło się na kolejne reformy edukacji i 2 razy 2 już nie będzie się równać 4?

Spieszę wszystkich uspokoić. Prawa matematyki są niezmienne i to, co odkryte, zostaje na zawsze. Zmienia się tylko zakres badań, tematyka, metody i najważniejsze: punkt widzenia. Co jest ważne, a co może być schowane na strych albo do piwnicy odkryć matematycznych?

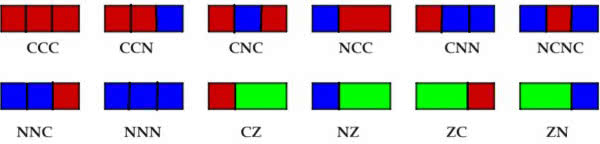
Jednym z nowych tematów jest wszystko, co jest związane z „tiling” – układaniem kafelków. Najbardziej znane są odkrycia Roberta Penrose’a. Zachęcam Czytelnika do obejrzenia efektownych układanek – setki ornamentów są oczywiście do znalezienia w sieci. A ja skupię się na czymś bardzo, ale to bardzo prostym. Mamy prostokąt rozmiaru 1 na n i trzy rodzaje kafelków; dwa różne kwadratowe (powiedzmy czerwony i niebieski) i jeden rodzaj 1×2 (powiedzmy zielony).

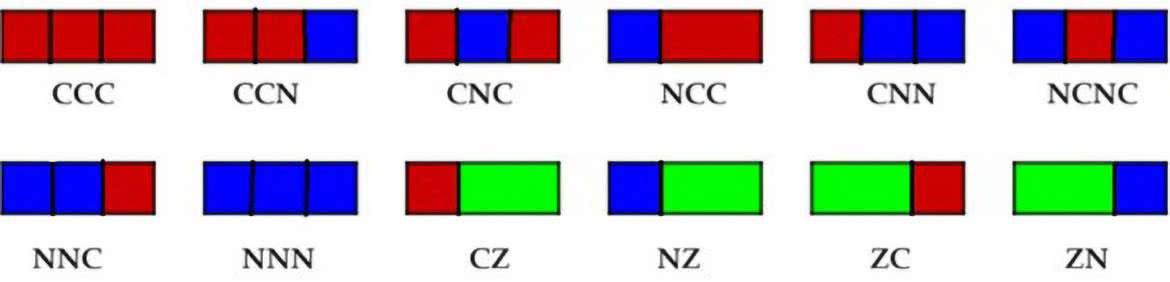
Na ile sposób możemy wypełnić nasz prostokąt takimi kafelkami? Dla n=1 mamy dwa sposoby: kafelek czerwony albo kafelek niebieski. Gdy n=2 (a więc mamy prostokąt 1×2), jest aż pięć sposobów (7).

7.

Dla prostokąta dłuższego o jeden kafelek liczba ta wzrasta do… zgadnij, Czytelniku! Tak jest, masz rację: do dwunastu! Bo przecież piątka i dwunastka tak się lubią (8).

8.

Zadanie dla Czytelników: proszę sprawdzić, że wy-razy tego ciągu spełniają zależność

a(n+1)=2a(n)+a(n–1)

A tych młodych Czytelników, którzy będą zdawać w tym roku maturę rozszerzoną z matematyki, poproszę o formalny dowód metodą indukcji matematycznej.

Po raz kolejny wrócę do lat sześćdziesiątych XX wieku. Teorią grafów mało kto się wtedy interesował. Problematyka wystrzeliła w kilkanaście lat później – ze względów jak najbardziej praktycznych. Chodzi o wszechstronna analizę połączeń w sieciach. Trudności obliczeniowe są znaczne – bez komputera nie da się wiele zdziałać.

9.

Sprawdziłem, czy chatGPT zna się i na tym. Ponieważ wiedziałem, jaki ma być wynik, nie dałem się oszukać. Za trzecią próbą podał (podała, podało?) mi właściwe rozwiązanie. Można je przetworzyć tak.

Ile jest grafów (spójnych, to jest „w jednym kawałku”) czterech wierzchołkach? Pięć, oto one:

Każdy zgadnie, że skoro piszę o tym, to następnych grafów (o pięciu wierzchołkach) będzie dwanaście (10)!

10.

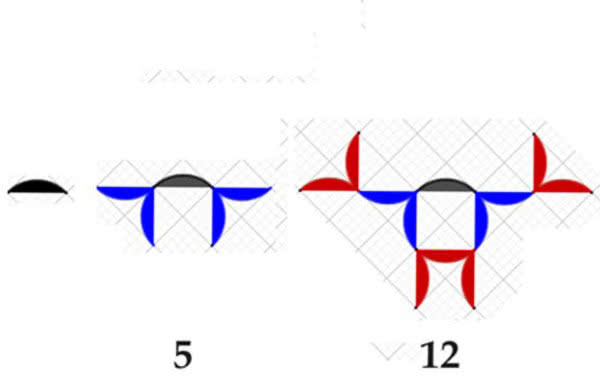
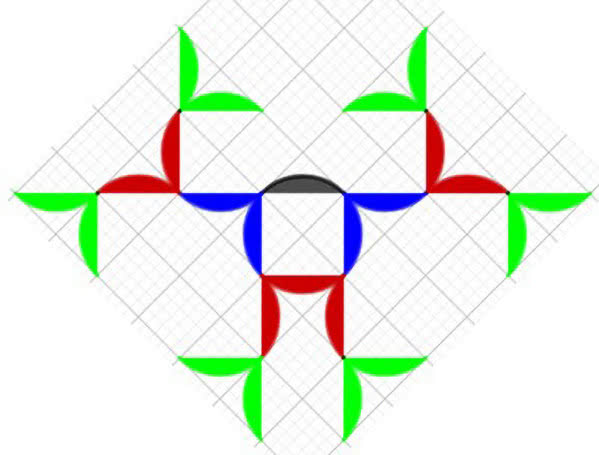
Na tym nie koniec. Z wielu innych przykładów wspomnę o przyjaźni 5–12 w ciągu, który w literaturze nazywa się Q-toothpick sequence (czyli ciąg Q-wykałaczek), ale ja wymyśliłem nazwę P-ciąg. Litera P pochodzi od pterodaktyla, prehistorycznego gada latającego. Spójrzmy zresztą na rysunek 9. W drugiej jego części zobaczyć można ptaka, może ważkę, może lądujący samolot sportowy. Następnie to już jakieś drapieżne ptaszysko, ale potem to już raczej rozrastający się kwiat. Regułę dołączania nowych gałązek łatwo zrozumieć z tego rysunku. Każdy koniec gałązki wypuszcza dwa nowe pędy. Przypomina to ciąg Fibonacciego, który zaczyna się od 0 i 1, a każdy następny wyraz jest sumą dwóch poprzednich.

11.

Za moich czasów studenckich ciąg Fibonacciego nazywaliśmy ciągiem stołówkowym: każdy obiad w stołówce studenckiej był sumą dwóch poprzednich.

Czytelnik znów może mieć wątpliwości. „Owszem, to ciekawe łamigłówki, ale przecież nic więcej. Krzyżówki i sudoku też bywają trudne”.

12.

Jak pisałem, wszystko to ma związek z badaniami połączeń w sieciach. Ciąg wykałaczkowy („z pterodaktylem”) jest poza tym przykładem „automatu komórkowego”. Już sama nazwa wskazuje, że może to być coś ważnego w informatyce. Najbardziej znanym automatem komórkowym jest gra Life, wymyślona ok. 1970 roku przez brytyjskiego matematyka Johna Conwaya, a spopularyzowana w kilka lat później w amerykańskim „Scientific American”. Nie jest to gra w ścisłym tego słowa znaczeniu. Podajemy początkowy układ komórek, a potem „życie” toczy się samo. Kto nie zna tej gry – bardzo polecam się z nią zapoznać. Jest wciągająca i tajemnicza. Niemal jak samo prawdziwe życie, ale już nie mam miejsca, by niej pisać dokładniej. Mam tylko nadzieję, że zaciekawiłem Czytelnika niektórymi aspektami tajemniczej przyjaźni dwóch liczb, piątki i dwunastki. Napisanie jednej za drugą też daje ciekawy efekt: 512=2⁸, a 125=5³. 

Michał Szurek